浙江省宁波市海曙区2023年中考一模数学试卷

试卷更新日期：2023-04-25 类型：中考模拟

进入出卷网下载

一、选择题(每小题4分，共40分)

1. 下列实数中，最大的是（）

A、2 B、 $- \frac{1}{2}$ C、 $\sqrt{2}$ D、0

查看试题解析
2. 下列计算正确的是（）

A、(x²)³=x⁵ B、x²·x³=x⁶ C、x³+x³=2x³ D、x³÷x³=x

查看试题解析
3. 2022年世界杯在卡塔尔举办，为了办好这届世界杯，人口仅有280万的卡塔尔投资2200亿美元修建各项设施，数据2200亿用科学记数法表示为（）

A、 $22 \times 1 0^{10}$ B、 $2.2 \times 1 0^{10}$ C、 $2.2 \times 1 0^{11}$ D、 $0.22 \times 1 0^{12}$

查看试题解析
4. 在水平的桌面上放置着一个如图所示的物体，则它的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 抢微信红包已成为中国传统节日人们最喜爱的祝福方式，今年春节期间，某人在自己的微信群中发出红包，一共有 10名好友抢到红包，抢到红包的金额情况如表：
金额(元)
4
4.5
5
5.5
6
8
人数(人)
1
3
2
1
2
1
则10名好友抢到金额的众数、中位数分别是（）

A、4.5元，5元 B、4.5元，6元 C、8元，4.5元 D、5元，4.5元

查看试题解析
6. 对于分式 $\frac{2 - x}{2 x - 6}$ 下列说法错误的是（）

A、当x=2时，分式的值为0 B、当x=3时，分式无意义 C、当x>2时，分式的值为正数 D、当x= $\frac{8}{3}$ 时，分式的值为1

查看试题解析
7. 我国民间流传着-道数学问题：只闻隔壁人分银，不知多少银和人：每人7两多7两，每人半斤少半斤(注；古代1斤=16两)．试问各位善算者，多少人分多少银．设有m人，分n两银，根据题意列二元一次方程组正确的是（）

A、 ${\begin{cases} 7 n + 7 = m \\ 8 n - 8 = m \end{cases}$ B、 ${\begin{cases} 7 m + 7 = n \\ 8 m + 8 = n \end{cases}$ C、 ${\begin{cases} 7 n - 7 = m \\ 8 n - 8 = m \end{cases}$ D、 ${\begin{cases} 7 m + 7 = n \\ 8 m - 8 = n \end{cases}$

查看试题解析
8. 下列说法正确的是（）

A、两组对角分别相等的四边形是平行叫边形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线相等的四边形是矩形 D、两条对角线垂直且相等的四边形是正方形

查看试题解析
9. 如图矩形ABCD由矩形EBGF逆时针旋转一个锐角得到，点C在边EF上，过点E作AD平行线得矩形ANMD，则要知道矩形ANMD的面积只需知道（）

A、S_△_BEC B、S_△B_GC C、S_△E_CM D、S_△C_GF

查看试题解析
10. 某容器由A、B、C三段圆柱体组成(如图①)，其中A、B、C的底面积分别为5S，2S，S(单位：cm²)，C段的容积是容器总容积的 $\frac{1}{4}$ ，现以速度v(单位：cm³/s)匀速向容器注水，直至注满为止．图②是注水全过程中容器的水面高度h (单位：cm)与注水时间t (单位：s)的函数图象．下列说法错误的是（）

A、a=10 B、b=24 C、c=10 D、v=2S

查看试题解析

二、填空题(每小题5分，共30分)

11. 口袋里有两个红球一个白球，随机摸出一个球结果是红球的概率是．

查看试题解析
12. 二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是。

查看试题解析
13. 若(a-2)²+ $\sqrt{b + 3}$ =0，则(a+b)²⁰²³的值是．

查看试题解析
14. 圆锥侧面展开图的半径为6cm，圆心角为120°，则该圆锥的底面半径长为．

查看试题解析
15. 如图，点A (7 $\sqrt{2}$ ， 7 $\sqrt{2}$ )，过A作AB⊥x轴于点B，C是反比例函数y= $\frac{24}{x}$ 图像上一动点且在△AOB内部，以C为圆心 $\sqrt{2}$ 为半径作⊙C，当⊙C与△AOB的边相切时，点C的纵坐标是．

查看试题解析
16. 如图，在矩形ABCD中，AB=9，E为CD上一点，tan∠EAD= $\frac{1}{3}$ ，以E为圆心，EA为半径的弧交AB于F，交BC于G，若F为弧AG的中点，则AF= ， tan∠GEC=.

查看试题解析

三、解答题(第17，18，19题每题8分，第20，21，22题每题10分，第23题12分，第24题14分，共80分)

17.

(1)、计算(π-3)⁰+| $\sqrt{3}$ -2|-( $\frac{1}{3}$ )^-1

(2)、先化简，再求值：(5m+4)(5m-4)-5m(5m-6)，其中m= $\frac{1}{6}$

查看试题解析
18. 如图，△ABC的三个顶点分别在正方形网格的格点上，请按要求完成下列各题：

(1)、在图①中找一格点D，连结BD，使∠ABD与∠BAC互补；

(2)、在图②中找一格点E，连结BE，使∠ABE与∠BAC互余；．

(3)、在图③中找一格点F，连结BF，使∠ABF=45°

查看试题解析
19. 如图①是一把折叠躺椅，其示意图如图②所示，其中DE平行地面，人们可通过调整∠FDE和∠DEG的大小来满足不同需求，经测量两支脚AB=AC=50cm，支点D在AC上且AD=10cm，椅背DF=80cm，躺椅打开时两支脚的夹角∠BAC=80°．

(1)、求躺椅打开时两支脚端点B、C之间的距离：

(2)、躺椅打开时，调整椅背使∠EDF=140°，求此时椅背的最高点F到地面的距离．
(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84)

查看试题解析

20. 为了让学生更好地掌握疫情防控知识，增强疫情防控意识，某市中学生举行了一次“疫情防控知识竞赛”，共有16000 名中学生参加了这次竞赛，为了解本次竞赛成绩情况，从中随机抽取了部分学生的成绩进行统计，得到下表并绘制如图所示不完整的统计图．

分组	分数段	频数	频率
A	50≤x<60	40	0.08
B	60≤x<70	80	0.16
C	70≤x<80	100	0.2
D	80≤x<90	a	0.32
E	90≤x≤100	120	b

根据上面提供的信息，解答下列问题：

(1)、a= ， b= ；补全频数分布直方图；

(2)、被抽取学生的成绩的中位数落在分数段上；

(3)、若竞赛成绩在80分以上(含80分)的学生为优秀．请估计该市参加“疫情防控知识竞赛”成绩为优秀的学生人数．

查看试题解析

21. 某次干旱灾情，甲地急需抗早用水15万吨，乙地13万吨，现有A、B两水库决定各调出14万吨水支援甲、乙两地抗早，已知从A水库到甲地50千米，到乙地30千米：从B水库到甲地60千米，到乙地45千米

(1)、设从A水库调往甲地水量为x万吨，完成下表，并直接写出x的取值范围是 .

调入地水量/万吨调出地	甲	乙	总计
A	x		14
B			14
总计	15	13	28

(2)、若调运水的费用为200元/万吨·千米，求调运总费用W的最小值．

查看试题解析

22. 对于抛物线y=ax²-4x+3(a>0)

(1)、若抛物线过点(4，3)
①求顶点坐标；

②当0≤x≤6时，直接写出y的取值范围为；

(2)、已知当0≤x≤m时，1≤y≤9，求a和m的值．

查看试题解析
23. 已知 E在△ABC内部(如图①)，等边三角形ABC的边长为6，等边三角形BDE的边长为4，连结AE和DC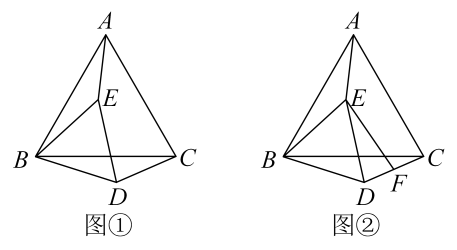

(1)、求证AE=DC；

(2)、当AE⊥BD时，求CD的长；

(3)、将△BDE绕点B旋转一周，F为DC的中点(如图②)，求旋转过程中EF的取值范围．

查看试题解析
24. 定义，若四边形的一条对角线平分这个四边形的面积，则称这个四边形为倍分四边形，这条对角线称为这个四边形的倍分线。如图①，在四边形ABCD中，若S_△_ABC=S_△_ADC ，则四边形ABCD为倍分四边形，AC为四边形ABCD的倍分线

(1)、判断：若是真命题请在括号内打√，若是假命题请在括号内打×
①平行四边形是倍分四边形（）
②梯形是倍分四边形（）

(2)、如图①，倍分四边形ABCD中，AC是倍分线，若AC⊥AB，AB=3，AD=DC=5，求BC；

(3)、如图②，△ABC中BA=BC，以BC为直径的00分别交AB、AC于点N、M，已知四边形BCMN是倍分四边形。
①求sinC；
②连结BM，CN交于点D，取OC中点F，连结MF交NC于E(如图③)，若OF=3，求DE．

查看试题解析

金额(元)	4	4.5	5	5.5	6	8
人数(人)	1	3	2	1	2	1