江苏省淮安市2022-2023学年七年级下学期期中数学试题
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 生物具有遗传多样性,遗传信息大多储存在分子上.一个分子的直径约为.这个数量用科学记数法表示为( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,由下列条件能判定的是( )
 A、 B、 C、 D、4. 已知三角形的三边长分别为3,5, , 则不可能是( )A、3 B、5 C、7 D、85. 如果一个多边形的内角和等于 , 那么这个多边形的边数为( )A、7 B、8 C、9 D、106. 已知某正方形的面积是(16-8x+x2)cm2(x>4),则该正方形的周长是( )A、(4-x)cm B、(x-4)cm C、(16-4x)cm D、(4x-16)cm7. 将一副三角尺按如图所示的位置摆放,其中O,E,F在直线l上,点B恰好落在边上, , , . 则的度数为( )
A、 B、 C、 D、4. 已知三角形的三边长分别为3,5, , 则不可能是( )A、3 B、5 C、7 D、85. 如果一个多边形的内角和等于 , 那么这个多边形的边数为( )A、7 B、8 C、9 D、106. 已知某正方形的面积是(16-8x+x2)cm2(x>4),则该正方形的周长是( )A、(4-x)cm B、(x-4)cm C、(16-4x)cm D、(4x-16)cm7. 将一副三角尺按如图所示的位置摆放,其中O,E,F在直线l上,点B恰好落在边上, , , . 则的度数为( ) A、 B、 C、 D、8. 如图,现有 , 两类正方形卡片和类长方形卡片各若干张,如果要拼成一个长为 , 宽为的大长方形,那么需要类卡片张数为( )
A、 B、 C、 D、8. 如图,现有 , 两类正方形卡片和类长方形卡片各若干张,如果要拼成一个长为 , 宽为的大长方形,那么需要类卡片张数为( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题
-
9. 分解因式:a2+a= .10. 若 , , 则.11. 如果展开后的结果不含x的一次项,则m的值是.12. 如图表示钉在一起的木条a,b,c.若测得 , 要使木条 , 木条a至少要旋转°.
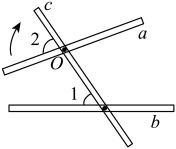 13. 如图, , , 平分 , 则的度数是.
13. 如图, , , 平分 , 则的度数是. 14. 若是一个完全平方式,则m的值为.15. 计算:=.16. 如图,在中,已知点E、F分别是边上的中点,且 , 则的值为.
14. 若是一个完全平方式,则m的值为.15. 计算:=.16. 如图,在中,已知点E、F分别是边上的中点,且 , 则的值为. 17. 对于实数a,b,c,d,规定一种运算 =ad-bc,如 =1×(-2)-0×2=-2,那么当 =27时,则x=.18. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《解:九章算法》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
17. 对于实数a,b,c,d,规定一种运算 =ad-bc,如 =1×(-2)-0×2=-2,那么当 =27时,则x=.18. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《解:九章算法》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为.
三、解答题
-
19. 计算:(1)、;(2)、;20. 先化简,再求值: , 其中 , .21. 如图,的三个顶点都在正方形网格的格点上(网格中每个小正方形的边长都为1个单位长度),将平移,使点A平移到的位置.
 (1)、画出平移后的;(2)、连接 , 则线段与线段的关系是;(3)、线段在平移的过程中扫过的图形面积为.22. 如下,这是一道例题的部分解答过程,其中A,B是两个关于x,y的二项式.
(1)、画出平移后的;(2)、连接 , 则线段与线段的关系是;(3)、线段在平移的过程中扫过的图形面积为.22. 如下,这是一道例题的部分解答过程,其中A,B是两个关于x,y的二项式.例题:化简:
解:原式=
____.(注意:运算顺序从左到右,逐个去掉括号)
请仔细观察上面的例题及解答过程,完成下列问题:
(1)、多项式A为 , 多项式B为 , 例题的化简结果为;(2)、求多项式A与B的积.23. 定义一种幂的新运算: , 请利用这种运算规则解决下列问题:(1)、的值为;(2)、若 , 求的值;24. 如图,点F在线段上,点E,G在线段上, , . (1)、求证:;(2)、若于点H,平分 , , 则的度数为.25. 在图1中,三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)、求证:;(2)、若于点H,平分 , , 则的度数为.25. 在图1中,三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形. (1)、根据图2中的阴影部分面积关系直接写出下列代数式 , , 之间的数量关系:;(2)、根据完全平方公式的变形,解决下列问题:
(1)、根据图2中的阴影部分面积关系直接写出下列代数式 , , 之间的数量关系:;(2)、根据完全平方公式的变形,解决下列问题:①已知 , , 求和的值;
②已知 , 则的值为 ▲ .
26. 在我们苏科版义务教育教科书数学七下第42页曾经研究过双内角平分线的夹角和内外角平分线夹角问题.聪聪在研究完上面的问题后,对这类问题进行了深入的研究,他的研究过程如下: (1)、【问题再现】
(1)、【问题再现】如图1,在△ABC中,∠ABC、∠ACB的角平分线交于点P,若∠A=50°.则∠P=;
(2)、【问题推广】如图2,在△ABC中,∠BAC的角平分线与△ABC的外角∠CBM的角平分线交于点P,过点B作BH⊥AP于点H,若∠ACB=80°,求∠PBH的度数.
(3)、如图3,在△ABC中,∠ABC、∠ACB的角平分线交于点P,将△ABC沿DE折叠使得点A与点P重合,若∠1+∠2=100°,则∠BPC=;(4)、【拓展提升】在四边形BCDE中,EBCD,点F在直线ED上运动(点F不与E,D两点重合),连接BF,CF,∠EBF、∠DCF的角平分线交于点Q,若∠EBF=α,∠DCF=β,直接写出∠Q和α,之间的数量关系.