湖北省武汉市武昌区七校联考2022-2023学年七年级下学期数学期中试题
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 下列实数中最小的是( )A、 B、 C、 D、2. 计算:的平方根等于( )A、 B、 C、 D、3. 下列命题为真命题的有( )
①内错角相等;②无理数都是无限小数:③在同一平面内,过一点有且只有一条直线与已知直线垂直;④过一点有且只有一条直线与已知直线平行
A、0个 B、1个 C、2个 D、3个4. 已知M(1,﹣2),N(﹣3,﹣2),则直线MN与x轴,y轴的位置关系分别为( )A、相交,相交 B、平行,平行 C、垂直,平行 D、平行,垂直5. 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AB∥CE,且∠ADC=∠B,④AB∥CE,且∠BCD=∠BAD;其中能推出BC∥AD的条件为( )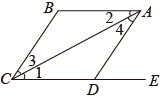 A、①② B、②④ C、②③ D、②③④6. 如图, , 于点C,的延长线与交于点E,若 , 则等于( )
A、①② B、②④ C、②③ D、②③④6. 如图, , 于点C,的延长线与交于点E,若 , 则等于( ) A、 B、 C、 D、7. 已知点P(2 - a,3a + 6)到两标轴距离相等,则点P的坐标为( )A、(3,3) B、(6,-6) C、(3,3)或(6,-6) D、(3,-3)8. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )
A、 B、 C、 D、7. 已知点P(2 - a,3a + 6)到两标轴距离相等,则点P的坐标为( )A、(3,3) B、(6,-6) C、(3,3)或(6,-6) D、(3,-3)8. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )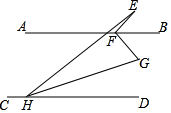 A、90° B、95° C、100° D、150°9. 如图,长方形的各边分别平行于x轴或y轴,物体甲和物体乙分别由点 , 同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以4个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2023次相遇地点的坐标是( )
A、90° B、95° C、100° D、150°9. 如图,长方形的各边分别平行于x轴或y轴,物体甲和物体乙分别由点 , 同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以4个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2023次相遇地点的坐标是( ) A、 B、 C、 D、10. 如图,已知 , 点E,F分别在直线上,点P在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为( )
A、 B、 C、 D、10. 如图,已知 , 点E,F分别在直线上,点P在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为( ) A、 B、 C、或 D、或或
A、 B、 C、或 D、或或二、填空题
-
11. 化简:.12. 若 , , 则.13. 已知点在x轴上,则点P坐标是.14. 若同一平面内的与 , 一组边互相平行,另一组边互相垂直,且比的2倍少 , 则的度数=.15. 已知点 , , 将线段平移到线段 , 若点A的对应点C落在x轴上,点B的对应点D落在y轴上,则线段与y轴的交点P经过平移后对应点的坐标为.16. 如图,已知长方形纸片 , 点E,F在BC边上,点G,H在边上,分别沿折叠,点B和点C 恰好都落在点P处.若 , 则.

三、解答题
-
17. 计算:(1)、(2)、18. 求下列式子中的x的值:(1)、(2)、19. 填空完成推理过程:
如图:已知 , , 求证:.

证明:∵( )
∴ ▲ ( )
∴( )
∵
∴ ▲ ( )
∴( )
∴.( )
20. 已知的算术平方根为5,立方根为 , 求的平方根.21. 作图题:(利用无刻度的直尺作图)如图,在方格纸中,有两条线段.利用方格纸完成以下操作:

( 1 )过点A作的平行线;
( 2 )过点C作的平行线,与(1)中的平行线交于点D;
( 3 )过点B作的垂线;
( 4 )请在上找一点P,使得线段平分三角形的面积,在图上作出线段.
22. “比差法”是数学中常用的比较两个数大小的方法,即:;
例如:比较与2的大小.
∵ 又∵ 则
∴ ,
∴.
请根据上述方法解答以下问题:
(1)、的整数部分是 , 的小数部分是;(2)、比较与的大小.(3)、已知 , 试用“比差法”比较与的大小.23. 已知直线 , E、F分别为直线上的点,P为直线上方一点.(1)、如图1,若 , , 求的度数. (2)、如图2,的角平分线的反向延长线与的角平分线交于点N,试说明:.(不能利用三角形的内角和)
(2)、如图2,的角平分线的反向延长线与的角平分线交于点N,试说明:.(不能利用三角形的内角和) (3)、如图3,若的角平分线与的角平分线交于点H,的角平分线与的角平分线交于点G,当时,请写出与之间的数量关系,并说明理由.
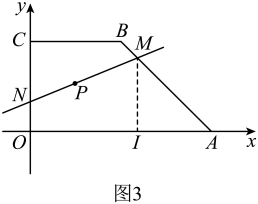
(3)、如图3,若的角平分线与的角平分线交于点H,的角平分线与的角平分线交于点G,当时,请写出与之间的数量关系,并说明理由. 24. 已知四边形顶点坐标分别为 , , .(1)、如图1,若将四边形向下平移2个单位,O、A、B、C的对应点分别为E、F、G、H,此时图中的阴影部分面积为14,求与x轴的交点M坐标.
24. 已知四边形顶点坐标分别为 , , .(1)、如图1,若将四边形向下平移2个单位,O、A、B、C的对应点分别为E、F、G、H,此时图中的阴影部分面积为14,求与x轴的交点M坐标. (2)、如图2,在(1)的条件下,连接 , 若点P是坐标轴上一点,且三角形与三角形的面积相等,请求出P点坐标.
(2)、如图2,在(1)的条件下,连接 , 若点P是坐标轴上一点,且三角形与三角形的面积相等,请求出P点坐标. (3)、如图3,已知是四边形内一点,过P点的直线交线段于M,交y轴的正半轴于N,设M、N的纵坐标分别为m、n,则当直线平分四边形的面积时,请直接写出m与n之间的数量关系.
(3)、如图3,已知是四边形内一点,过P点的直线交线段于M,交y轴的正半轴于N,设M、N的纵坐标分别为m、n,则当直线平分四边形的面积时,请直接写出m与n之间的数量关系.