湖北省武汉市江夏区2022-2023学年七年级下学期期中考试数学试卷
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 的立方根是( )A、 B、2 C、 D、42. 下列各数:3.14159, , , , 0,无理数有( )个A、1 B、2 C、3 D、43. 下列等式正确的是( )A、 B、 C、 D、4. 如果m是任意实数,则点 一定不在A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 将一块三角板沿一条直角边所在的直线向右平移个单位到位置,如图所示.下列结论:①且;②且;③;④若 , , 则边边扫过的图形的面积为5,正确的个数有( )
 A、4 B、3 C、2 D、16. 满足的整数x的个数是( )A、4个 B、5个 C、6个 D、7个7. 已知点 , , , 且轴,轴,则的平方根为( )A、2 B、 C、4 D、8. 如图,将长方形纸片沿折叠后,若 , 则的度数为( )
A、4 B、3 C、2 D、16. 满足的整数x的个数是( )A、4个 B、5个 C、6个 D、7个7. 已知点 , , , 且轴,轴,则的平方根为( )A、2 B、 C、4 D、8. 如图,将长方形纸片沿折叠后,若 , 则的度数为( )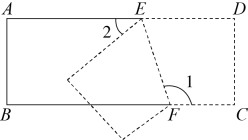 A、 B、 C、 D、9. 下列命题是真命题的是( )A、过一点有且只有一条直线和已知直线平行 B、 , 则 C、与互为相反数,则与互为相反数 D、的平方根是210. 如图,与交于点 , 点在直线上,交于点 , , , .下列说法中:①;②;③;④ , 其中正确的是( )
A、 B、 C、 D、9. 下列命题是真命题的是( )A、过一点有且只有一条直线和已知直线平行 B、 , 则 C、与互为相反数,则与互为相反数 D、的平方根是210. 如图,与交于点 , 点在直线上,交于点 , , , .下列说法中:①;②;③;④ , 其中正确的是( )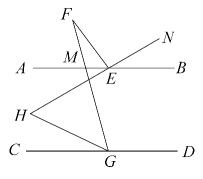 A、①② B、①④ C、①②④ D、②④
A、①② B、①④ C、①②④ D、②④二、填空题
-
11. 的相反数是;的绝对值是;.12. 已知点A在x轴上方,到x轴的距离是3,到y轴的距离是4,那么点A的坐标是。
13. 与的两边分别平行,是余角的3倍.则.14. 已知 , 则的值为.15. 如图, , , 于 , 则的度数是度. 16. 已知平面直角坐标系中, , , , 延长与轴交于一点 , 若 , 则点的坐标为.
16. 已知平面直角坐标系中, , , , 延长与轴交于一点 , 若 , 则点的坐标为.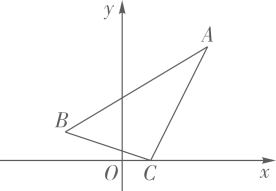
三、解答题
-
17. 计算(1)、;(2)、.18. 已知点 , 解答下列各题:(1)、点在轴上,求出点的坐标;(2)、点的坐标为 , 直线轴,求出点的坐标;(3)、若点在第二象限,且它到轴的距离与轴的距离相等,求的值.19. 根据题意将下列空格补充完整:
如图, , , .
求证:.

证明:∵
∴ ▲ ( )
∴( )
▲ (两直线平行,内错角相等)
∵ ,
∴ ▲ ( )
∴( )
∴( )
20. 如图,AB∥ CD,E是直线FD上的一点, ∠ ABC= , ∠CDF= .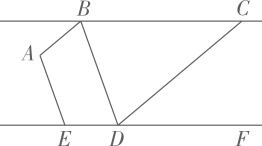 (1)、求证:BC ∥ EF;(2)、连接BD,若BD∥ AE, ∠BAE= ,则BD是否平分 ∠ABC ?请说明理由.21. 如图,组成的正方形网格的每个小方格的边长都为单位1,每一个小方格的顶点叫做格点.已知点A、、、都在格点上.请按下述要求画图并回答问题:
(1)、求证:BC ∥ EF;(2)、连接BD,若BD∥ AE, ∠BAE= ,则BD是否平分 ∠ABC ?请说明理由.21. 如图,组成的正方形网格的每个小方格的边长都为单位1,每一个小方格的顶点叫做格点.已知点A、、、都在格点上.请按下述要求画图并回答问题: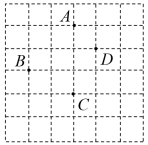 (1)、建立适当的平面直角坐标系,使点的坐标为;(2)、在(1)的条件下,完成下列问题:
(1)、建立适当的平面直角坐标系,使点的坐标为;(2)、在(1)的条件下,完成下列问题:①过点作 , , 并写出点的坐标;
②在网格中轴的下方找出所有的格点 , 使 , 并写出格点的坐标;
③线段交轴于点 , 求点的坐标.
22. 如图,用两个面积为的小正方形纸片拼成一个大正方形.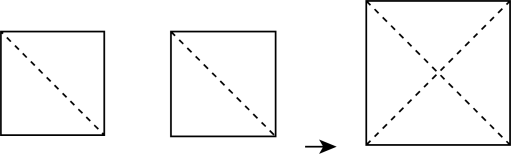 (1)、求拼成的大正方形纸片的边长;(2)、若沿此大正方形纸片的边的方向剪出一个长方形,能否使剪出的长方形纸片的长、宽之比为且面积为?若能,试求出剪出的长方形的长与宽;若不能,请说明理由.23. 已知直线 , 、分别在直线、上,为平面里一点,连接、.
(1)、求拼成的大正方形纸片的边长;(2)、若沿此大正方形纸片的边的方向剪出一个长方形,能否使剪出的长方形纸片的长、宽之比为且面积为?若能,试求出剪出的长方形的长与宽;若不能,请说明理由.23. 已知直线 , 、分别在直线、上,为平面里一点,连接、.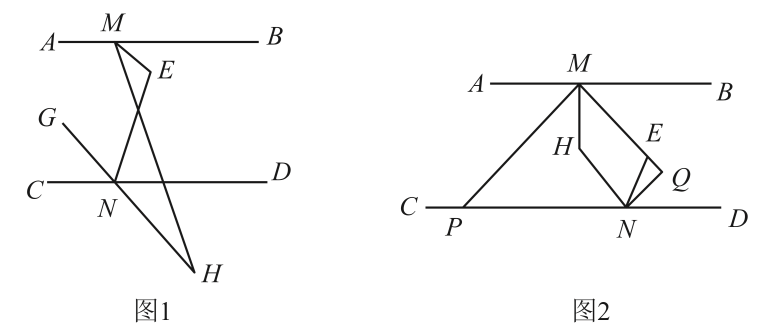 (1)、如图1,延长至 , 和的角平分线相交于点.
(1)、如图1,延长至 , 和的角平分线相交于点.①若 , , 则的度数为 ▲ ;
②探究与的数量关系,并给予证明;
(2)、如图2,与的角平分线相交于点 , 作平分交于 , 交的延长线于点 , 若 , 求的度数.24. 在平面直角坐标系中,点、分别是轴和轴的正半轴上的点,点在第一象限,它们的坐标分别是 , , , 且满足. (1)、直接写出四边形的面积;(2)、点是轴上一个动点,当的面积等于8时,求点的坐标;(3)、将线段平移至线段(点的对应点为 , 点的对应点为),且点在线段上,当的面积为时,求点的坐标.
(1)、直接写出四边形的面积;(2)、点是轴上一个动点,当的面积等于8时,求点的坐标;(3)、将线段平移至线段(点的对应点为 , 点的对应点为),且点在线段上,当的面积为时,求点的坐标.