福建省三明市永安市2022-2023学年八年级下学期期中数学卷
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 下列四组线段中,可以构成直角三角形的是( )A、1, , B、2,3,4 C、1,2,3 D、4,5,62. 与2的差不大于0,用不等式表示为( )A、 B、 C、 D、3. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、4. 关于x的一元一次不等式x-3<0的解集在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、 5. 下列定理中没有逆定理的是( )A、内错角相等,两直线平行 B、对顶角相等 C、等腰三角形两底角相等 D、直角三角形中,两锐角互余6. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
5. 下列定理中没有逆定理的是( )A、内错角相等,两直线平行 B、对顶角相等 C、等腰三角形两底角相等 D、直角三角形中,两锐角互余6. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
7. 如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )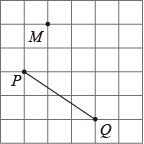 A、(2,3) B、(3,3) C、(4,2) D、(5,1)8. 如下图,地面上有三个洞口A、B、C,老鼠可从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口,尽快抓住老鼠,应该蹲在( )
A、(2,3) B、(3,3) C、(4,2) D、(5,1)8. 如下图,地面上有三个洞口A、B、C,老鼠可从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口,尽快抓住老鼠,应该蹲在( ) A、三条角平分线的交点 B、三条边的中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点9. 已知不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、10. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
A、三条角平分线的交点 B、三条边的中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点9. 已知不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、10. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( ) A、①② B、②③ C、①③ D、①②③
A、①② B、②③ C、①③ D、①②③二、填空题
-
11. 如果一个等腰三角形的两边长分别为2和4,则第三边的长为.12. 关于 的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为.
 13. 已知五个正数的和等于5,用反证法证明这五个数中至少有一个大于或等于1,其中,第一步应假设.14. 如图,直线与轴、轴的交点分别为 , , 则关于的不等式的解集为.
13. 已知五个正数的和等于5,用反证法证明这五个数中至少有一个大于或等于1,其中,第一步应假设.14. 如图,直线与轴、轴的交点分别为 , , 则关于的不等式的解集为. 15. 如图,在中, , , , 将沿射线方向平移2个单位后得到 , 连接 , 则的长为.
15. 如图,在中, , , , 将沿射线方向平移2个单位后得到 , 连接 , 则的长为. 16. 如图,已知中, , , , 点、分别在线段、上,将沿直线折叠,使点A的对应点恰好落在线段上,当为直角三角形时,线段的长为.
16. 如图,已知中, , , , 点、分别在线段、上,将沿直线折叠,使点A的对应点恰好落在线段上,当为直角三角形时,线段的长为.
三、解答题
-
17. 下面是小彬求解一元一次不等式及自我检查的过程,请认真阅读并完成相应的任务.
解答过程
自我检查
解:去分母,得 . …第一步去括号,得 . …第二步
移项,得 . …第三步
合并同类项,得 . …第四步
系数化为1,得 . …第五步
第一步正确,其依据是____;
第二步符合去括号法则,也正确;
第三步出错了!
(1)、第一步的依据是不等式的一条性质,请写出这一性质的内容:(2)、第三步出错的原因是:;(3)、请从第三步开始,写出正确解答过程.18. 解不等式组 , 并把它的解集在数轴上表示出来 19. 用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使 , 再过点M画的垂线,过点N画的垂线,两垂线交于点P,那么射线就是的平分线.请你证明这一结论.
19. 用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使 , 再过点M画的垂线,过点N画的垂线,两垂线交于点P,那么射线就是的平分线.请你证明这一结论. 20. 如图,在中, , 在同一平面内,将绕点逆时针旋转到的位置,连接 , 求证:.
20. 如图,在中, , 在同一平面内,将绕点逆时针旋转到的位置,连接 , 求证:.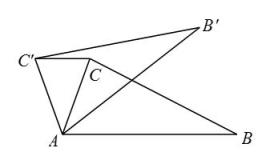 21. 如图,方格纸中每个小正方形边长都是1个单位长度.的三个顶点 , , .
21. 如图,方格纸中每个小正方形边长都是1个单位长度.的三个顶点 , , .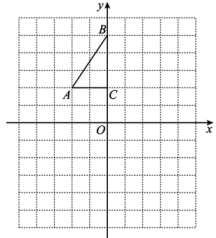 (1)、将以点为旋转中心顺时针旋转 , 得到 , 请画出并写出点的坐标;(2)、平移 , 使点的对应点坐标为 , 请画出平移后对应的 , 并写出点的坐标;(3)、若将绕某一点旋转可得到 , 则旋转中心点的坐标为.22. 命题:等腰三角形底边中点到两腰的距离相等.请你依据所给图形,写出已知,求证,并证明它是定理.
(1)、将以点为旋转中心顺时针旋转 , 得到 , 请画出并写出点的坐标;(2)、平移 , 使点的对应点坐标为 , 请画出平移后对应的 , 并写出点的坐标;(3)、若将绕某一点旋转可得到 , 则旋转中心点的坐标为.22. 命题:等腰三角形底边中点到两腰的距离相等.请你依据所给图形,写出已知,求证,并证明它是定理.
已知:
求证:
证明:
23. 如图,在中,. (1)、在边上找一点 , 使;(尺规作图,保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若 , , 求的长.24. 某村在政府的扶持下建起了鲜花大棚基地,准备种植 , 两种鲜花。经测算,种植两种鲜花每亩的投入与获利情况如下表:
(1)、在边上找一点 , 使;(尺规作图,保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若 , , 求的长.24. 某村在政府的扶持下建起了鲜花大棚基地,准备种植 , 两种鲜花。经测算,种植两种鲜花每亩的投入与获利情况如下表:每亩需投入(万元)
每亩可获利(万元)
种鲜花
2
0.8
种鲜花
4
1.2
(1)、政府和村共同投入200万元全部用来种植这两种鲜花,总获利万元.设种植种鲜花亩,求关于的函数关系式;(2)、在(1)的条件下,若要求A种鲜花的种植面积不能多于B种鲜花种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.25. 在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放,其中 , , .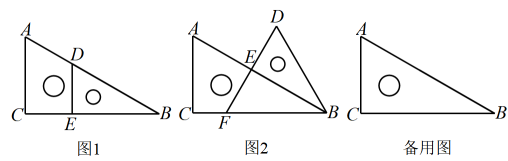 (1)、;(2)、小昕同学将三角板绕点按顺时针方向旋转.
(1)、;(2)、小昕同学将三角板绕点按顺时针方向旋转.(i)如图2,当点落在边上时,延长交于点 , 求的长.
(ii)若点、、在同一条直线上,请画出示意图并求点到直线的距离.