福建省福州市晋安区2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 下列二次根式,属于最简二次根式的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 在中, , , 的对应边分别是 , , , 下列条件不能说明是直角三角形的是( )A、 B、 C、 D、4. 如图,菱形的对角线相交于点 , , , 则菱形的面积为( )
 A、 B、 C、 D、5. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、6. 下列逆命题成立的是( )A、两条直线平行,内错角相等 B、全等三角形的对应角相等 C、如果 , 那么 D、如果 , 那么7. 如图,在中,点 , 分别是 , 边上的中点,连接 , 如果 , 那么的长是( )
A、 B、 C、 D、5. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、6. 下列逆命题成立的是( )A、两条直线平行,内错角相等 B、全等三角形的对应角相等 C、如果 , 那么 D、如果 , 那么7. 如图,在中,点 , 分别是 , 边上的中点,连接 , 如果 , 那么的长是( ) A、 B、 C、 D、8. 如图,菱形的顶点在直线上,若 , , 则的度数为( )
A、 B、 C、 D、8. 如图,菱形的顶点在直线上,若 , , 则的度数为( ) A、 B、 C、 D、9. 已知在平面直角坐标系中,矩形的三个顶点的坐标为 , , , 则第四个顶点的坐标为( )A、 B、 C、( D、10. 在平行四边形中,为的中点,点 , 为平行四边形同一边上任意两个不重合的动点(不与端点重合), , 的延长线分别与平行四边形的另一边交于点 , .下面四个判断:
A、 B、 C、 D、9. 已知在平面直角坐标系中,矩形的三个顶点的坐标为 , , , 则第四个顶点的坐标为( )A、 B、 C、( D、10. 在平行四边形中,为的中点,点 , 为平行四边形同一边上任意两个不重合的动点(不与端点重合), , 的延长线分别与平行四边形的另一边交于点 , .下面四个判断:①四边形是平行四边形;
②四边形是平行四边形;
③若平行四边形是矩形(正方形除外),则至少存在一个四边形ENFM是正方形;
④对于任意的平行四边形 , 存在无数个四边形是矩形.
其中,正确的个数有( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 二次根式有意义,则的取值范围是.12. 在 Rt △ABC中, ∠ACB=90°,AC=6,BC=8,D是AB的中点,则 .13. 如图,在正方形外作等边 , 则.
 14. 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=.
14. 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=. 15. 如图,已知菱形的边长为 , , 为的中点,若为对角线上一动点,则的最小值为.
15. 如图,已知菱形的边长为 , , 为的中点,若为对角线上一动点,则的最小值为.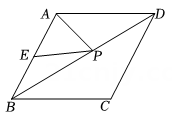 16. 如图,四边形中, , 且 , 以、、为边向外作正方形,其面积分别为 , , , 若 , 则的值为.
16. 如图,四边形中, , 且 , 以、、为边向外作正方形,其面积分别为 , , , 若 , 则的值为.
三、解答题
-
17. 计算:(1)、;(2)、.18. 先化简,再求值: , 其中.19. 如图,在平行四边形 中,E、F是对角线上的两点,且. 求证:四边形是平行四边形.
 20. 如图,在中, , 为的高,求的长.
20. 如图,在中, , 为的高,求的长.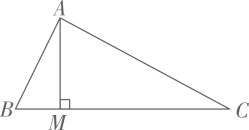 21. 求证:四个角都相等的四边形是矩形.(根据题意画出图形,并写出已知、求证和证明过程)22. 如图,已知四边形是平行四边形.
21. 求证:四个角都相等的四边形是矩形.(根据题意画出图形,并写出已知、求证和证明过程)22. 如图,已知四边形是平行四边形. (1)、尺规作图:按下列要求完成作图;(保留作图痕迹,请标注字母)
(1)、尺规作图:按下列要求完成作图;(保留作图痕迹,请标注字母)①连接;
②作的垂直平分线交 , 于 , ;
③连接 , ;
(2)、判断四边形的形状,并说明理由.23. 在一个数学活动中,若身旁没有量角器或者三角尺,又需要作 , , 的角,可以采用如下的方法:【操作感知】
第一步:对折矩形纸片 , 使与重合,得到折痕 , 把纸片展开.
第二步;再一次折叠纸片,使点落在上,并使折痕经过点 , 得到折痕 , 同时得到线段(如图1).
 (1)、【猜想论证】
(1)、【猜想论证】
写出图1中一个的角:.(2)、若延长交于点 , 如图所示,试判断的形状,并证明.(3)、【迁移探究】
小华将矩形纸片换正方形纸片,继续探究,过程如下:将正方形纸片按照操作感知的方式操作,并延长交于点 , 连接.当点在上时, , 求正方形的边长.
