陕西省西安市长安区2023年中考数学模拟试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 的平方根是( )A、 B、 C、 D、
-
2. 两位数,十位数字是x,个位数字比十位数字的2倍少3,这个两位数是( )A、x(2x﹣3) B、x(2x+3) C、12x﹣3 D、12x+3
-
3. 在下列各式中,不是代数式的是( )A、7 B、 C、 D、
-
4. 已知:a× =b×1 =c÷ ,且a、b、c都不等于0,则a、b、c中最小的数是( )A、a B、b C、c D、a和c
-
5. 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
 A、2 B、 C、 D、
A、2 B、 C、 D、 -
6. 如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,BF=7cm,则EC长为( )
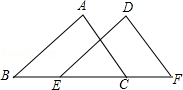 A、1cm B、2cm C、3cm D、4cm
A、1cm B、2cm C、3cm D、4cm -
7. 三角形两边长分别为4和6,第三边是方程x2-13x+36=0的根,则三角形的周长为( )A、14 B、18 C、19 D、14或19
-
8. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
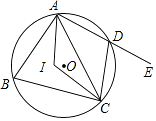 A、56° B、62° C、68° D、78°
A、56° B、62° C、68° D、78°
二、填空题
-
9. 若点和点关于x轴对称,则=
-
10. 计算:.
-
11. 当x为时, 的值为﹣1.
-
12. 已知|sinA-|+=0,那么∠A+∠B=.
-
13. 已知 , 为一元二次方程 的两根,那么 的值为.
三、解答题
-
14. 已知 , 求的值
-
15. 计算:
-
16. 解一元二次方程:
-
17. 如图,已知扇形 , 请用尺规作图,在上求作一点P,使(保留作图痕迹,不写作法).
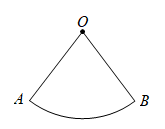
-
18. 某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
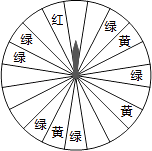 (1)、求转动一次转盘获得购物券的概率;(2)、转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
(1)、求转动一次转盘获得购物券的概率;(2)、转转盘和直接获得购物券,你认为哪种方式对顾客更合算? -
19. 某公司其有名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成如下统计图表进行分析.
频率分布表
组别
销售数量(件)
频数
频率
A
B
C
D
E
合计

请根据以上信息,解决下列问题:
(1)、频数分布表中,a=、b=:(2)、补全频数分布直方图;(3)、如果该季度销量不低于80件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数. -
20. 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高与影子长正好相等;接着李明沿方向继续向前走,走到点B处时,李明直立时身高的影子恰好是线段 , 并测得 , 已知李明直立时的身高为 , 求路灯的高的长.(结果精确到.
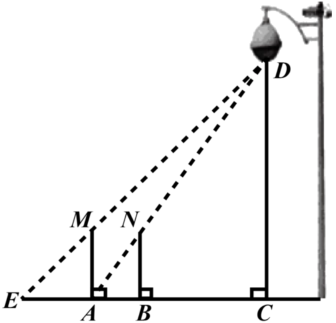
-
21. 已知n边形的对角线共有 条(n是不小于3的整数);(1)、五边形的对角线共有条;(2)、若n边形的对角线共有35条,求边数n;(3)、若n边形的边数增加1,对角线总数增加9,求边数n.
-
22. 如图,在 中,内角 所对的边分别为 .
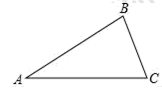 (1)、若 ,请直接写出 与 的和与 的大小关系;(2)、求证: 的内角和等于 ;(3)、若 ,求证: 是直角三角形.
(1)、若 ,请直接写出 与 的和与 的大小关系;(2)、求证: 的内角和等于 ;(3)、若 ,求证: 是直角三角形. -
23. 如图,已知一次函数y=kx+b的图象与反比例函数y= 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
 (1)、求一次函数的解析式;(2)、求△AOB的面积.
(1)、求一次函数的解析式;(2)、求△AOB的面积. -
24. 某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图
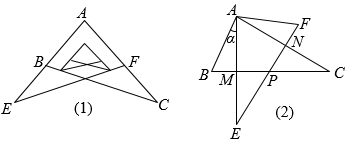 (1)、所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)、所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.求证:AM=AN;
(2)、当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由. -
25. 如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
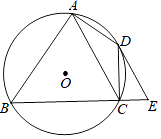 (1)、求证:DE是⊙O的切线;(2)、若AC∥DE,当AB=8,CE=2时,求AC的长.
(1)、求证:DE是⊙O的切线;(2)、若AC∥DE,当AB=8,CE=2时,求AC的长. -
26. 如图,已知抛物线y=-x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
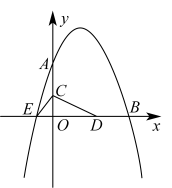 (1)、直接写出抛物线的解析式:;(2)、求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?(3)、当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
(1)、直接写出抛物线的解析式:;(2)、求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?(3)、当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
