四川省成都市高新区2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. -5的倒数是A、 B、5 C、 D、-52. 2023年春节期间,我省文化和旅游经济呈现“总体回暖,强势复苏”的可喜局面,其中体现巴蜀文化风韵的川渝春晚网络话题反响热烈,累计阅读量超过亿人次.将数据亿用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 已知直线 , 将含有的直角三角尺按如图方式放置(),其中A,C两点分别落在直线m,n上,若 , 则的度数为( )
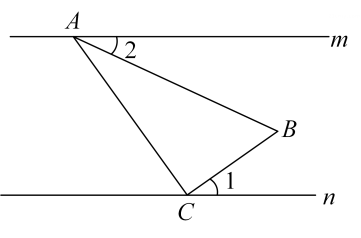 A、 B、 C、 D、5. 若 , 且 , 若的周长为 , 则的周长为( )A、 B、 C、 D、6. 校运会100米项目预赛,15名运动员的成绩各不相同,取前8名参加决赛,其中运动员小米已经知道自己的成绩,他想确定自己是否进入决赛,只需要知道这15名运动员成绩的( )A、平均数 B、中位数 C、极差 D、方差7. 《九章算术》是我国古代重要的数学专著之一,其中记录了一道驿站送信的题目,大意为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天.已知快马的速度是慢马的倍,求规定时间.设规定时间为x天,则可列出正确的方程为( )A、 B、 C、 D、8. 关于二次函数 , 下列说法正确的是( )A、图象的对称轴在y轴右侧 B、y的最小值为5 C、图象与x轴有两个交点 D、当时,y的值随x的值的增大而增大
A、 B、 C、 D、5. 若 , 且 , 若的周长为 , 则的周长为( )A、 B、 C、 D、6. 校运会100米项目预赛,15名运动员的成绩各不相同,取前8名参加决赛,其中运动员小米已经知道自己的成绩,他想确定自己是否进入决赛,只需要知道这15名运动员成绩的( )A、平均数 B、中位数 C、极差 D、方差7. 《九章算术》是我国古代重要的数学专著之一,其中记录了一道驿站送信的题目,大意为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天.已知快马的速度是慢马的倍,求规定时间.设规定时间为x天,则可列出正确的方程为( )A、 B、 C、 D、8. 关于二次函数 , 下列说法正确的是( )A、图象的对称轴在y轴右侧 B、y的最小值为5 C、图象与x轴有两个交点 D、当时,y的值随x的值的增大而增大二、填空题
-
9. 化简分式的结果为 .10. 已知直线过点和 , 则ab(填“>”、“<”或“=”).11. 如图,已知每一个小正方形的边长为1,则△ABC的面积为 .
 12. 若关于x的一元二次方程 有两个不相等的实数根,则k 的取值范围是.13. 如图,的周长为 , 连接 , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线 , 交边于点E,连接 , 则的周长为 .
12. 若关于x的一元二次方程 有两个不相等的实数根,则k 的取值范围是.13. 如图,的周长为 , 连接 , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线 , 交边于点E,连接 , 则的周长为 .
三、解答题
-
14.(1)、计算:;(2)、解不等式组:15. 幸福成都,美在文明!为助力成都争全国文明典范城市,某校采用四种宣传形式:A.宣传单宣传,B.电子屏宣传,C.黑板报宣传,D.志愿者宣传.每名学生从中选择一种最喜欢的宣传形式,学校就最喜欢的宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)、本次调查的学生共有 人,请补全条形统计图;(2)、扇形统计图中,“D.志愿者宣传”对应的扇形圆心角度数为;(3)、本次调查中,在最喜欢“志愿者宣传”的学生中,有甲、乙、丙、丁四位同学表现优秀,若从这四位同学中随机选出两名同学参加学校的志愿者活动,请用列表或画树状图的方法,求选出两人恰好是甲和乙的概率16. 成都新世纪环球中心被誉为亚洲第一大单体建筑,可容纳20个悉尼歌剧院,3个五角大楼.某校开展综合实践活动,测量环球中心主体顶端A离地面的高度的长,如图,在观测点C处测得建筑物顶端A的仰角为 , 在观测点C测得建筑物底部B的俯角为 , 观测点C与建筑物的水平距离为120米,且垂直于(点A,B,C,D在同一平面内).求环球中心主体顶端A离地面的高度的长.(结果精确到1米;参考数据: , , , ) 17. 如图,在中, , 以为直径的与交于点D,与边交于点E,过点D作的垂线,垂足为F.
17. 如图,在中, , 以为直径的与交于点D,与边交于点E,过点D作的垂线,垂足为F. (1)、求证:为的切线;(2)、若 , , 求的半径及的值.18. 在平面直角坐标系中,直线与反比例函数的图象交于点和点B.
(1)、求证:为的切线;(2)、若 , , 求的半径及的值.18. 在平面直角坐标系中,直线与反比例函数的图象交于点和点B. (1)、求反比例函数的表达式;(2)、如图1,若点C为线段上一点,过点C作轴交双曲线于点D,连接 , 若的面积为 , 求点C的坐标;(3)、如图2,连接 , 并延长至点E,使 , 作的平分线交x轴于点F,过点E作于点H,求点H的坐标.
(1)、求反比例函数的表达式;(2)、如图1,若点C为线段上一点,过点C作轴交双曲线于点D,连接 , 若的面积为 , 求点C的坐标;(3)、如图2,连接 , 并延长至点E,使 , 作的平分线交x轴于点F,过点E作于点H,求点H的坐标.四、填空题
-
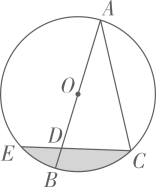
19. 若 ,则 的值为.20. 若关于x的分式方程的解为非负数,则a的取值范围是 .21. 如图,是的直径,为弦, , D为直径上一点,且 , 连接并延长交于点E,现假设可以随意在圆中取点,则这个点取在阴影部分的概率是 .
 22. 如图,抛物线与x轴交于两点,抛物线上点C的横坐标为 , D点坐标为 , 连接 , 点M为平面内任意一点,将绕点M旋转得到对应的(点的对应点分别为 , , ),若中恰有两个点落在抛物线上,则此时点的坐标为(点不与点A重合)
22. 如图,抛物线与x轴交于两点,抛物线上点C的横坐标为 , D点坐标为 , 连接 , 点M为平面内任意一点,将绕点M旋转得到对应的(点的对应点分别为 , , ),若中恰有两个点落在抛物线上,则此时点的坐标为(点不与点A重合)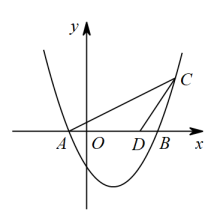 23. 如图,在矩形中, , , 点P为边上一动点,连接交对角线于点E,过点作 , 交于点F,连接交于点G,在点P的运动过程中,面积的最小值为 .
23. 如图,在矩形中, , , 点P为边上一动点,连接交对角线于点E,过点作 , 交于点F,连接交于点G,在点P的运动过程中,面积的最小值为 .
五、解答题
-
24. 某文具店经销甲、乙两种笔记本,每次购买同一种笔记本的单价相同,购进笔记本的具体信息如下表:
进货批次
甲种笔记本数量(单位:本)
乙种笔记本数量(单位:本)
购买总费用(单位:元)
第一次
第二次
(1)、求甲、乙两种笔记本的购买单价;(2)、若第三次计划用不超过元购买甲、乙两种笔记本共本,求至少购买甲种笔记本多少本?25. 在平面直角坐标系中,抛物线与x轴交于A,B两点(点A在点B的左侧),直线与抛物线交于C,D两点(点D在第一象限). (1)、如图,当点C与点A重合时,求抛物线的函数表达式;(2)、在(1)的条件下,连接 , 点E在抛物线上,若 , 求出点E的坐标;(3)、将抛物线L向上平移1个单位得到抛物线 , 抛物线的顶点为P,直线与抛物线交于M,N两点,连接 , 若 , 求a的值.26. 在矩形中, , , 点M为边上一点,连接 .
(1)、如图,当点C与点A重合时,求抛物线的函数表达式;(2)、在(1)的条件下,连接 , 点E在抛物线上,若 , 求出点E的坐标;(3)、将抛物线L向上平移1个单位得到抛物线 , 抛物线的顶点为P,直线与抛物线交于M,N两点,连接 , 若 , 求a的值.26. 在矩形中, , , 点M为边上一点,连接 . (1)、将沿直线翻折,得到对应的 .
(1)、将沿直线翻折,得到对应的 .i)如图1,延长交边于点E,若点E恰为边中点,求线段的长;
ii)如图2,连接 , 若 , 求线段的长;
(2)、如图3,若 , 点P为边上一动点(点P不与B,C两点重合),过点P作交线段于点F,在点P的运动过程中,线段的长是否存在最大值,若存在,求出这个最大值;若不存在,请说明理由.