陕西省宝鸡市凤翔区2023年九年级下学期第一次质检数学试题

试卷更新日期：2023-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 如图， $A B ∥ C D$ ， $E C$ 平分 $∠ A E F$ ，且 $∠ A E C = 65 °$ ，则 $∠ E F D$ 的大小为（）

A、 $100 °$ B、 $120 °$ C、 $130 °$ D、 $140 °$

查看试题解析
3. 计算 ${(- 2 m^{2} n^{3})}^{2}$ 的结果是（）

A、 $- 2 m^{4} n^{6}$ B、 $4 m^{4} n^{6}$ C、 $4 m^{4} n^{5}$ D、 $- 4 m^{4} n^{5}$

查看试题解析
4. 一次函数 $y = - 2 x + 3$ 的图象向上移2个单位长度后，与 $y$ 轴相交的点坐标为（）

A、 $(0 ， 5)$ B、 $(0 ， 1)$ C、 $(5 ， 0)$ D、 $(1 ， 0)$

查看试题解析
5. 如图， $A B$ 为 $⊙ O$ 的直径，C，D为 $⊙ O$ 上的两点，若 $∠ B A C = 68 °$ ，则 $∠ D$ 的度数为（）

A、 $68 °$ B、 $34 °$ C、 $32 °$ D、 $22 °$

查看试题解析
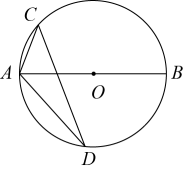6. 2022年世界杯足球赛举世瞩目，某大型企业为奖励年度优秀员工，预定了小组赛和决赛两个阶段的门票共20张作为奖品，总价为74000元.已知小组赛门票每张2800元，决赛门票每张6400元，设该企业预定了小组赛门票x张，决赛门票y张，根据题意可列方程组为（）

A、 ${\begin{array}{l} x + y = 20 \\ 2800 x + 6400 y = 74000 \end{array}$ B、 ${\begin{array}{l} x + y = 20 \\ 6400 x + 2800 y = 74000 \end{array}$ C、 ${\begin{array}{l} x - y = 20 \\ 2800 x + 6400 y = 74000 \end{array}$ D、 ${\begin{array}{l} x + y = 20 \\ 6400 y = 74000 + 2800 x \end{array}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $t a n B = 1$ ， $s i n C = \frac{1}{2}$ ， $A B = \sqrt{2}$ ，则边 $B C$ 的长为（）

A、 $2 \sqrt{3} - 1$ B、 $\sqrt{3} + 1$ C、 $\sqrt{2} + 1$ D、 $2 \sqrt{2} - 1$

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c$ ，其中y与x的部分对应值如下表.
$x$
…
0
1
2
3
4
5
…
$y$
…
$- 3$
$- 4$
$- 3$
0
5
12
…
则下列结论中正确的是（）

A、 $a b c < 0$ B、 $\frac{b}{2 a} = 1$ C、 $4 a + 2 b + c > 0$ D、方程 $a x^{2} + b x + c = 0$ 的两个根分别是 $x_{1} = - 1$ ， $x_{2} = 3$

查看试题解析

二、填空题

9. 实数a，b在数轴上的位置如图所示，则 $a + b$ 0.

查看试题解析
10. 正六边形的每个内角等于°．

查看试题解析
11. 如图，在菱形 $A B C D$ 中， $∠ A B C = 6 0^{∘}$ ， $A B = 4$ ，对角线交于点O，F，E分别是 $A D$ ， $B O$ 的中点，则线段 $E F$ 的长度为.

查看试题解析
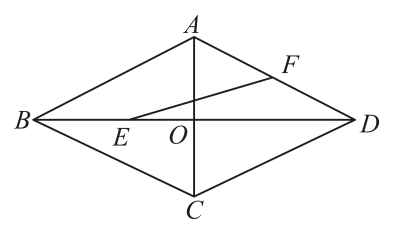12. 如图，点D是矩形 $A O B C$ 的对称中心， $A (0 ， 6)$ ， $B (8 ， 0)$ ，若反比例函数 $y = \frac{k}{x}$ 的图象经过点D，交 $A C$ 于点M，则点M的坐标为.

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， D是 $A B$ 的中点，连接 $C D$ ，过点B作 $C D$ 的垂线，交 $C D$ 延长线于点E， $t a n A = \frac{4}{3}$ ，则 $c o s ∠ D B E$ 的值为.

查看试题解析

三、解答题

14. 计算： $2 \times (- 1) + | \sqrt{3} - 2 | + {(π - 3)}^{0}$ .

查看试题解析
15. 解不等式组： ${\begin{array}{l} - \frac{3}{2} x - 1 < 2 ① \\ 2 (x - 1) \leq x + 4 ② \end{array}$

查看试题解析
16. 化简： $(\frac{x}{x - 3} - 1) \div \frac{9}{x^{2} - 6 x + 9}$ .

查看试题解析
17. 如图，在 $△ A B C$ 中，点D在 $A B$ 边上， $A D = 4 B D$ ，请用尺规作图法，在 $A C$ 边上找一点E，使 $C E = \frac{1}{5} A C$ .（不写作法，保留作图痕迹）

查看试题解析
18. 如图，在 $△ A B C$ 中，D是 $B C$ 边上一点， $D E ∥ A C ，$ $C B = D E$ ， $∠ A B C = ∠ E$ ，求证： $A C = B D$ .

查看试题解析
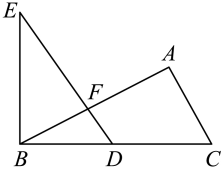19. 如图，在 $1 \times 1$ 的正方形网格中有 $△ A B C$ ，在网格中建立平面直角坐标系后，点 $B$ 的坐标为 $(- 2 ， - 2)$ ，点C的坐标为 $(2 ， 0)$ ，按要求解答下列问题：

(1)、在图中画出正确的平面直角坐标系.

(2)、 $A B$ 的长度为.

查看试题解析
20. 从一副扑克牌中取出四张牌，他们的牌面数字分别为1，2，2，3，将这四张扑克牌背面朝上洗匀，从中随机抽取一张，记录下数字后放回，称为抽牌一次.

(1)、若随机抽牌一次，抽到数字2的概率为.

(2)、将这四张扑克牌背面朝上洗匀，从中随机抽取一张，不放回；再从剩余的三张牌中随机抽取一张.请利用“列表”或“画树状图”的方法，求抽取的这两张牌的牌面数字之和为偶数的概率.

查看试题解析
21. 如图，小刚同学从楼顶A处看楼下公园的湖边D处的俯角为 $65 °$ ，看另一边B处的俯角为 $25 °$ ，楼高 $A C$ 为 $25$ 米，求楼下公园的湖宽 $B D$ .（结果精确到1米，参考数据： $s i n 25 ° \approx 0.42$ ， $t a n 25 ° \approx 0.47$ ， $s i n 65 ° \approx 0.91$ ， $t a n 65 ° \approx 2.14$ ）

查看试题解析
22. 甲，乙两家超市平时以同样的价格出售相同的商品，春节期间两家超市进行促销活动，促销方式如下：
甲超市：所有商品按原价打8折.
乙超市：一次购物不超过200元的按原价付款，超过200元后超过的部分打7折.

(1)、设分别在两家超市购买原价为 $x (x > 200)$ 元的商品后，实付金额为 $y_{甲}$ ， $y_{乙}$ 元，分别写出 $y_{甲}$ ， $y_{乙}$ 与x的函数关系式.

(2)、促销期间，若小刚一次购物的商品原价为500元，他去哪家超市购物更省钱？说明理由.

查看试题解析
23. 某校为了解八年级学生的身高状况，随机抽取40名男生、40名女生进行身高调查.根据所得数据绘制如下统计图表.根据图表中提供的信息，回答下列问题：
组别
身高 $x / c m$
A
$x < 150$
B
$150 \leq x < 155$
C
$155 \leq x < 160$
D
$160 \leq x < 165$
E
$x \geq 165$

(1)、求身高在 $150 \leq x < 155$ 之间的男生人数，并补全直方图.

(2)、男生身高的中位数落在组，女生身高的中位数落在组.（填组别字母序号）

(3)、已知该校八年级共有男生400人，女生420人，请估计八年级身高不足 $160 c m$ 的学生数.

查看试题解析
24. 如图， $△ B E F$ 内接于 $⊙ O$ ， $B E = B F$ ， $B O$ 的延长线交 $E F$ 于点D.C是 $⊙ O$ 外一点，连接 $O C$ ， $B C$ ， $O C ⊥ B E$ 于点A.已知 $O A = 2$ ， $A B = 4$ ， $A C = 8$ .

(1)、求证： $B C$ 是 $⊙ O$ 的切线.

(2)、求 $E F$ 的长.

查看试题解析
25. 跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段，运动员起跳后飞行的路线是抛物线的一部分（如图中实线部分所示），落地点在着陆坡（如图中虚线部分所示）上，着陆坡上的基准点K为飞行距离计分的参照点，落地点超过K点越远，飞行距离分越高.某滑雪赛场跳台滑雪的起跳台的高度 $O A$ 为 $60 m$ ，基准点K到起跳台的水平距离为 $70 m$ ，高度为 $18 m$ .设运动员从起跳点A起跳后的高度 $y (m)$ 与水平距离 $x (m)$ 之间的函数关系为 $y = - \frac{1}{50} x^{2} + b x + c$ .

(1)、若运动员落地点恰好到达K点，求b，c的值.

(2)、若运动员飞行的水平距离为 $21 m$ ，恰好达到最大高度 $68.82 m$ ，试判断他的落地点能否超过K点，并说明理由.

查看试题解析
26.

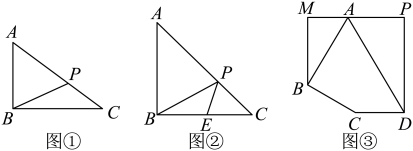(1)、问题提出
如图①，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A B = 5$ ， $B C = 12$ ，若P是边 $A C$ 上一点，则 $B P$ 的最小值为.

(2)、问题探究
如图②，在 $R t △ A B C$ 中， $A B = B C$ ，斜边 $A C$ 的长为 $4 \sqrt{2}$ ， E是 $B C$ 的中点，P是边 $A C$ 上一点，试求 $P B + P E$ 的最小值.

(3)、问题解决
某城区有一个五边形 $M B C D P$ 空地（ $∠ M = ∠ P = ∠ P D C = 90 °$ ， $∠ C = 150 °$ ），城建部门计划利用该空地建造一个居民户外活动广场，其中 $△ M A B$ 的部分规划为观赏区，用于种植各类鲜花， $△ A P D$ 部分规划为音乐区，供老年合唱团排练合唱或广场舞使用，四边形 $A B C D$ 部分为市民健身广场，如图③所示.已知 $A D = 100$ 米， $C D = 50$ 米， $∠ B A D = 60 °$ ， $∠ A B C = 90 °$ .为了进一步提升服务休闲功能，满足市民游园和健身需求，现要在 $A B$ ， $A D$ 上分别取点E，F，铺设一条由 $C E$ ， $E F$ ， $F C$ 连接而成的步行景观道，已知铺设景观道的成本为100元/米，求铺设完这条步行景观道所需的最低成本.

查看试题解析

组别	身高 $x / c m$
A	$x < 150$
B	$150 \leq x < 155$
C	$155 \leq x < 160$
D	$160 \leq x < 165$
E	$x \geq 165$

$x$	…	0	1	2	3	4	5	…
$y$	…	$- 3$	$- 4$	$- 3$	0	5	12	…