广西壮族自治区贵港市港北区2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 如果将“收入50元”记作“元”,那么“支出30元”记作( )A、元 B、元 C、元 D、元2. 所示的几何体是由个相同的小正方体搭成的,从正面看,所看到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 据报道:芯片被誉为现代工业的掌上明珠,芯片制造的核心是光刻技术,我国的光刻技术水平已突破到.已知 , 则用科学记数法表示是( )A、 B、 C、 D、4. 以下调查中,最适合采用抽样调查的是( )A、了解全国中学生的视力和用眼卫生情况 B、了解全班50名同学每天体育锻炼的时间 C、学校招聘教师,对应聘人员进行面试 D、为保证飞机正常飞行,对其零部件进行检查5. 下列运算,正确的是( )A、a+2a=3a2 B、a2•a3=a6 C、a3+a4=a12 D、(-3a)2=9a26. 下列对一元二次方程的根的情况判断中正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、不确定7. 如图,在⊙O中,∠BOC=130°,点A在 上,则∠BAC的度数为( )
3. 据报道:芯片被誉为现代工业的掌上明珠,芯片制造的核心是光刻技术,我国的光刻技术水平已突破到.已知 , 则用科学记数法表示是( )A、 B、 C、 D、4. 以下调查中,最适合采用抽样调查的是( )A、了解全国中学生的视力和用眼卫生情况 B、了解全班50名同学每天体育锻炼的时间 C、学校招聘教师,对应聘人员进行面试 D、为保证飞机正常飞行,对其零部件进行检查5. 下列运算,正确的是( )A、a+2a=3a2 B、a2•a3=a6 C、a3+a4=a12 D、(-3a)2=9a26. 下列对一元二次方程的根的情况判断中正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、不确定7. 如图,在⊙O中,∠BOC=130°,点A在 上,则∠BAC的度数为( ) A、55° B、65° C、75° D、130°8. 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )A、 B、 C、 D、9. 一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).
A、55° B、65° C、75° D、130°8. 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )A、 B、 C、 D、9. 一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计). A、π B、5π C、4π D、3π10. 在我国古代数学名著《算法统宗》里有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和身高为5尺的人一样高,秋千的绳索始终是拉直的,试问绳索有多长?”设绳索长为x尺,则x满足的方程为( )
A、π B、5π C、4π D、3π10. 在我国古代数学名著《算法统宗》里有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和身高为5尺的人一样高,秋千的绳索始终是拉直的,试问绳索有多长?”设绳索长为x尺,则x满足的方程为( ) A、x2=102+(x-5-1)2 B、x2=(x﹣5)2+102 C、x2=102+(x+1-5)2 D、x2=(x+1)2+10211. 如图,点和都在反比例函数的图象上,过点A分别向x轴y轴作垂线,垂足分别是M、N,连接、 , 若四边形的面积记作 , 面积记作 , 则( )
A、x2=102+(x-5-1)2 B、x2=(x﹣5)2+102 C、x2=102+(x+1-5)2 D、x2=(x+1)2+10211. 如图,点和都在反比例函数的图象上,过点A分别向x轴y轴作垂线,垂足分别是M、N,连接、 , 若四边形的面积记作 , 面积记作 , 则( )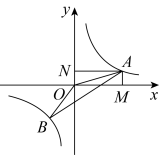 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 若分式有意义,则x的取值范围是.13. 因式分解:.14. 如图,在一束平行光线中插入一张对边平行的纸板.如果图中 是 ,那么 的度数是 .
 15. 随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为: , , , , 则小麦长势比较整齐的试验田是.16. 如图,在平面直角坐标系中,点A和B的坐标分别为(2,0),(0,-4),若将线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为
15. 随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为: , , , , 则小麦长势比较整齐的试验田是.16. 如图,在平面直角坐标系中,点A和B的坐标分别为(2,0),(0,-4),若将线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为 17. 如图,在菱形 中, ,将菱形 绕点 逆时针方向旋转,对应得到菱形 ,点 在 上, 与 交于点 ,则 的长是 .
17. 如图,在菱形 中, ,将菱形 绕点 逆时针方向旋转,对应得到菱形 ,点 在 上, 与 交于点 ,则 的长是 .
三、解答题
-
18. 解方程:19. 计算:.20. 如图,在边长为个单位长度的小正方形网格中,

( 1 )画出向上平移6个单位,再向右平移5个单位后的;
( 2 )以点B为位似中心,将放大为原来的2倍,得到 , 请在网格中画出;
( 3 )直接写出的面积,及 , 的坐标.
21. 2020年2月12日,教育部按照党中央关于防控新冠肺炎疫情的决策部署,对中小学延期开学期间“停课不停学”工作做出要求.某中学决定优化网络教学团队,整合初三年级为两个平行班(前进班和奋斗班)的学生提供线上授课,帮助毕业年级学生居家学习.经过一周时间的线上教学,学校通过线上测试了解网络教学的效果,从两个平行班中各随机抽取10名学生的成绩进行如下整理、分析(单位:分,满分100分):收集数据:
前进班:94,85,73,85,52,97,94,66,95,85
奋斗班:92,84,87,82,82,51,84,83,97,84
整理数据:
x(分)人数班级
前进班
1
1
a
3
b
奋斗班
1
0
0
7
2
分析数据:
平均数
众数
中位数
方差
前进班
82.6
85
c
194.24
奋斗班
82.6
d
84
132.04
根据以上信息回答下列问题:
(1)、请直接写出表格中a,b,c,d的值;(2)、已知小林同学的成绩为85分,在他们班处于中上水平,请问他是哪个班的学生?(3)、请你根据数据分析评价一下两个班的学习效果,说明理由.22. 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AM∥BD,交CB的延长线于点M. (1)、求证:△ADE≌△CBF;(2)、若四边形是BEDF菱形,AD=3,∠ABD=30°,求四边形AMBD的面积.23. “节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元;(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多.24. 如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)、求证:△ADE≌△CBF;(2)、若四边形是BEDF菱形,AD=3,∠ABD=30°,求四边形AMBD的面积.23. “节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元;(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多.24. 如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB. (1)、求证:PB是⊙O的切线;
(1)、求证:PB是⊙O的切线;
(2)、若∠APC=3∠BPC,求 的值.25. 如图,在平面直角坐标系中,抛物线 与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C.若线段 的长满足 ,则这样的抛物线称为“黄金”抛物线.如图,抛物线 为“黄金”抛物线,其与x轴交点为A,B(其中B在A的右侧),与y轴交于点C.且 (1)、求抛物线的解析式;(2)、若P为 上方抛物线上的动点,过点P作 ,垂足为D.
(1)、求抛物线的解析式;(2)、若P为 上方抛物线上的动点,过点P作 ,垂足为D.①求 的最大值;
②连接 ,当 与 相似时,求点P的坐标.