浙江省温州市永嘉县、苍南县、瓯海区2023年中考数学一模试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 计算的结果等于( )A、 B、 C、 D、2. 如图是由四个相同的小正方体组成的几何体,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 2022年温州市居民人均可支配收入约为63000元,其中数据63000用科学记数法表示为( )A、 B、 C、 D、4. 某校调查学生最喜爱的运动项目的统计图如图所示.若最喜欢足球的扇形统计图有60人,则最喜欢篮球的有( )
3. 2022年温州市居民人均可支配收入约为63000元,其中数据63000用科学记数法表示为( )A、 B、 C、 D、4. 某校调查学生最喜爱的运动项目的统计图如图所示.若最喜欢足球的扇形统计图有60人,则最喜欢篮球的有( )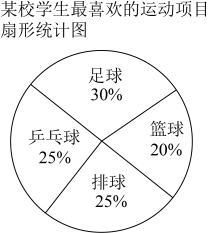 A、20人 B、40人 C、50人 D、60人5. 化简的结果是( )A、 B、 C、 D、6. 将方程去分母,结果正确的是( )A、 B、 C、 D、7. 若点 , , 均在抛物线上,则a,b,c的大小关系为( )A、 B、 C、 D、8. 一组同学一起去种树,如果每人种4棵,还剩下3棵树苗;如果每人种5棵,则缺少5棵树苗.设这组同学有x人,根据题意可列方程为( )A、 B、 C、 D、9. 如图,点A,B在x轴的正半轴上,以为边向上作矩形 , 过点D的反比例函数的图象经过的中点E.若的面积为1,则k的值为( )
A、20人 B、40人 C、50人 D、60人5. 化简的结果是( )A、 B、 C、 D、6. 将方程去分母,结果正确的是( )A、 B、 C、 D、7. 若点 , , 均在抛物线上,则a,b,c的大小关系为( )A、 B、 C、 D、8. 一组同学一起去种树,如果每人种4棵,还剩下3棵树苗;如果每人种5棵,则缺少5棵树苗.设这组同学有x人,根据题意可列方程为( )A、 B、 C、 D、9. 如图,点A,B在x轴的正半轴上,以为边向上作矩形 , 过点D的反比例函数的图象经过的中点E.若的面积为1,则k的值为( ) A、1 B、2 C、3 D、410. 将四个全等的三角形按如图所示的方式围成一个正方形 , 记的面积为 , 四边形的面积为.若 , , , 则图中阴影部分的面积为( )
A、1 B、2 C、3 D、410. 将四个全等的三角形按如图所示的方式围成一个正方形 , 记的面积为 , 四边形的面积为.若 , , , 则图中阴影部分的面积为( )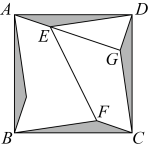 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:m2-6m+9= .12. 抛掷一枚质地均匀的正方体骰子1枚,朝上一面的点数为偶数的概率是 .13. 不等式的解为.14. 若扇形的圆心角为100°,半径为6,则它的弧长为.15. 如图,以菱形的顶点A为圆心,长为半径画弧,交对角线于点E.若 , , 则菱形的周长为.
 16. 如图1是一款轴对称“磁悬浮地漏”无水时的示意图,它由一个圆弧形密封盖与两个磁体组成(下侧磁体固定不动),连接杆与地面垂直,排水口 , 密封盖最高点E到地面的距离为 , 整个地漏的高度(G为磁体底部中点),密封盖被磁体顶起将排水口密封,所在圆的半径为;当有水时如图2所示,密封盖下移排水,当密封盖下沉至最低处时,点恰好落在中点,若点到的距离为 , 则密封盖下沉的最大距离为.
16. 如图1是一款轴对称“磁悬浮地漏”无水时的示意图,它由一个圆弧形密封盖与两个磁体组成(下侧磁体固定不动),连接杆与地面垂直,排水口 , 密封盖最高点E到地面的距离为 , 整个地漏的高度(G为磁体底部中点),密封盖被磁体顶起将排水口密封,所在圆的半径为;当有水时如图2所示,密封盖下移排水,当密封盖下沉至最低处时,点恰好落在中点,若点到的距离为 , 则密封盖下沉的最大距离为.
三、解答题
-
17.(1)、计算:.(2)、化简:.18. 如图,在的方格纸中,已知线段(A,B均在格点上),请按要求画出格点四边形(顶点均在格点上).
 (1)、在图1中画一个以为边的四边形 , 使其为轴对称图形.(2)、在图2中画一个以为对角线的四边形 , 使其为中心对称图形.19. 某校为迎接校庆活动,组织了九年级各班的合唱比赛,其中两个班的各项得分如下表:
(1)、在图1中画一个以为边的四边形 , 使其为轴对称图形.(2)、在图2中画一个以为对角线的四边形 , 使其为中心对称图形.19. 某校为迎接校庆活动,组织了九年级各班的合唱比赛,其中两个班的各项得分如下表:服装得体(分)
音准节奏(分)
形式创新(分)
九(1)班
90
78
85
九(2)班
75
92
84
(1)、如果将服装得体、音准节奏、形式创新三项得分按的比例确定各班的最终成绩,通过计算比较哪个班成绩更好?(2)、请你判断按(1)中分配比例是否合理.若合理,请说明理由;若不合理,请给出一个你认为合理的比例.20. 如图,在中,于点E,于点F. (1)、求证:.(2)、若 , , , 求的长.21. 已知二次函数的图象经过点.
(1)、求证:.(2)、若 , , , 求的长.21. 已知二次函数的图象经过点. (1)、求该函数的表达式,并在图中画出该函数的大致图象.(2)、P是该函数图象上一点,在对称轴右侧,过点作轴于点D.当时,求点P横坐标的取值范围.22. 如图,在中,D是上一点, , 以为直径的经过点C,交于点E,过点E作的切线交于点F.
(1)、求该函数的表达式,并在图中画出该函数的大致图象.(2)、P是该函数图象上一点,在对称轴右侧,过点作轴于点D.当时,求点P横坐标的取值范围.22. 如图,在中,D是上一点, , 以为直径的经过点C,交于点E,过点E作的切线交于点F. (1)、求证:.(2)、若 , , 求的长.23. 根据以下素材,探索完成任务.
(1)、求证:.(2)、若 , , 求的长.23. 根据以下素材,探索完成任务.如何设计奖品购买及兑换方案?
素材1
某文具店销售某种钢笔与笔记本,已知钢笔的单价是笔记本的2倍,用120元购买笔记本的数量比用160元购买钢笔的数量多8件.
素材2
某学校花费400元购买该文具店的钢笔和笔记本作为奖品颁发给“优秀学生”,
两种奖品的购买数量均不少于20件,且购买笔记本的数量是10的倍数.
素材3
学校花费400元后,文具店赠送m张兑换券(如右)用于商品兑换.兑换后,笔记本与钢笔数量相同.

问题解决
任务1
探求商品单价
请运用适当方法,求出钢笔与笔记本的单价.
任务2
探究购买方案
探究购买钢笔和笔记本数量的所有方案.
任务3
确定兑换方式
运用数学知识,确定一种符合条件的兑换方式.
24. 如图1,在矩形中, , .P,Q分别是 , 上的动点,且满足 , E是射线上一点, , 设 , . (1)、求y关于x的函数表达式.(2)、当中有一条边与垂直时,求的长.(3)、如图2,当点Q运动到点C时,点P运动到点F.连结 , 以 , 为边作.
(1)、求y关于x的函数表达式.(2)、当中有一条边与垂直时,求的长.(3)、如图2,当点Q运动到点C时,点P运动到点F.连结 , 以 , 为边作.①当所在直线经过点D时,求的面积;
②当点G在的内部(不含边界)时,直接写出x的取值范围.