浙江省宁波市2023年初中学业水平考试数学模拟试卷(探花卷)
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
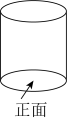
1. 在 , , , 这四个数中,最小的数是( )A、 B、 C、 D、2. 计算:的结果是( )A、 B、 C、 D、3. 2022年度全国电影总票房为亿元,数据亿用科学记数法表示为( )A、 B、 C、 D、4. 如图所示的圆柱体的俯视图为( )
 A、
A、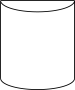 B、
B、 C、
C、 D、
D、 5. 某班30名学生的身高情况如下表所示,则这30名学生身高的中位数是( )
5. 某班30名学生的身高情况如下表所示,则这30名学生身高的中位数是( )身高(米)
1.45
1.48
1.50
1.53
1.56
1.60
人数
2
5
6
8
5
4
A、1.48米 B、1.53米 C、1.56米 D、1.60米6. 如图,已知 , 的弧长之差为 , , 则的长为( )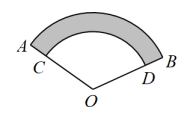 A、 B、 C、6 D、37. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、8. 已知二次函数的图象经过点 , , 在范围内有最大值为 , 最小值为 , 则的取值范围是( )A、 B、 C、 D、9. 如图,在等边三角形中, , 点D,F在上,点E在上.已知 , , 则的长为( )
A、 B、 C、6 D、37. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、8. 已知二次函数的图象经过点 , , 在范围内有最大值为 , 最小值为 , 则的取值范围是( )A、 B、 C、 D、9. 如图,在等边三角形中, , 点D,F在上,点E在上.已知 , , 则的长为( )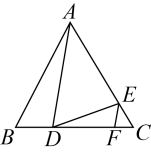 A、 B、 C、 D、10. 如图,在中, , 分别以 , , 为边在的同一侧作正方形 , , , 四块阴影部分的面积分别为 , , , .若已知图中阴影部分的面积的和,则一定能求出( )
A、 B、 C、 D、10. 如图,在中, , 分别以 , , 为边在的同一侧作正方形 , , , 四块阴影部分的面积分别为 , , , .若已知图中阴影部分的面积的和,则一定能求出( )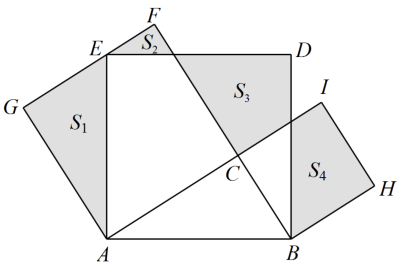 A、正方形的面积 B、正方形的面积 C、的面积 D、四边形的面积
A、正方形的面积 B、正方形的面积 C、的面积 D、四边形的面积二、填空题
-
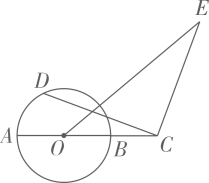
11. 实数的相反数是.12. 分解因式:.13. 一个不透明的袋子里装有9个球,其中2个红球,3个黄球,4个白球,它们除颜色外其余都相同.从袋子中任意摸出一个球是白球的概率为.14. 对于非零实数a,b,规定a⊕b= , 若(2x﹣1)⊕2=1,则x的值为 .15. 如图,在中,直径 , 延长至C,使 , 点D在上运动,连接 , 将绕点C顺时针旋转得到 , 连接 , 则线段的最大值为.
 16. 如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以OA,OC为边,在第一象限内作矩形OABC,且S矩形OABC=2 ,将矩形OABC翻折,使点B与原点O重合,折痕为MN,点C的对应点C'落在第四象限,过M点的反比例函数y= (k≠0)的图象恰好过MN的中点,则k的值为 , 点C'的坐标为 .
16. 如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以OA,OC为边,在第一象限内作矩形OABC,且S矩形OABC=2 ,将矩形OABC翻折,使点B与原点O重合,折痕为MN,点C的对应点C'落在第四象限,过M点的反比例函数y= (k≠0)的图象恰好过MN的中点,则k的值为 , 点C'的坐标为 .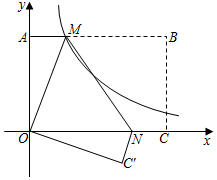
三、解答题
-
17.(1)、计算:.(2)、解不等式组:18. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点。如图,已知整A(2,2),B(4,1),请在所给网格区域(含边界)上找到整点P.
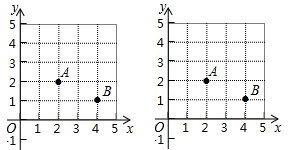 (1)、画一个等腰三角形PAB,使点P的纵坐标比点A的横坐标大1.(2)、若△PAB是直角三角形,则这样的点P共有个.19. 如图,一次函数的图象与反比例函数的图象相交于点.
(1)、画一个等腰三角形PAB,使点P的纵坐标比点A的横坐标大1.(2)、若△PAB是直角三角形,则这样的点P共有个.19. 如图,一次函数的图象与反比例函数的图象相交于点.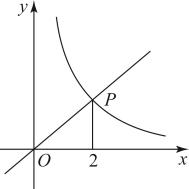 (1)、求m,k的值.(2)、直线与一次函数的图象相交于点A,与反比例函数的图象相交于点B.若的长为3,求a的值.20. 2022年10月12日,“天宫课堂”第三课开讲.神舟十四号飞行乘组生动演示了五个实验,分别为:A.毛细效应实验,B.水球变“懒”实验,C.太空趣味饮水实验,D.会调头的扳手实验,E.植物生长研究项目,某校随机抽取了部分学生对授课活动最感兴趣的实验进行了调查,并将统计结果绘制成如下统计表和统计图(不完整).
(1)、求m,k的值.(2)、直线与一次函数的图象相交于点A,与反比例函数的图象相交于点B.若的长为3,求a的值.20. 2022年10月12日,“天宫课堂”第三课开讲.神舟十四号飞行乘组生动演示了五个实验,分别为:A.毛细效应实验,B.水球变“懒”实验,C.太空趣味饮水实验,D.会调头的扳手实验,E.植物生长研究项目,某校随机抽取了部分学生对授课活动最感兴趣的实验进行了调查,并将统计结果绘制成如下统计表和统计图(不完整).实验
频数
频率
A
16
0.16
B
35
0.35
C
a
0.25
D
20
b
E
4
0.04
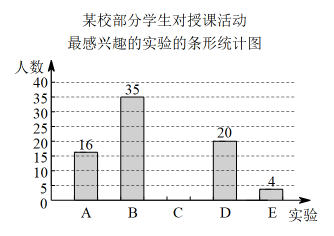
请根据上述信息,解答下列问题:
(1)、求出a,b的值并补全条形统计图.(2)、若该校有1200名学生,请你估计选择水球变“懒”实验的人数.(3)、假如你是一名宇航员,请根据以上调查结果,结合实际的实验操作,你会如何安排实验时间?简要说说你的想法.21. 如图,从点D处观测楼房的楼顶端点B的仰角为 , 从点D处沿着直线直走到达点E,从点E处观测楼顶端点B的仰角为 , 观测广告牌端点C的仰角为 , 求楼房的高度和广告牌的高度(结果精确到;参考数据: , , , , , , , , ).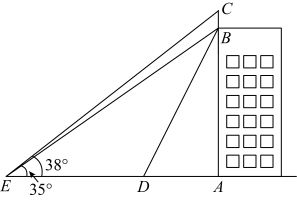 22. 某经销商销售一种成本价为100元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于180元/件.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
22. 某经销商销售一种成本价为100元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于180元/件.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:x
120
140
150
170
y
360
320
300
260
(1)、求y与x之间的函数表达式,并写出自变量x的取值范围.(2)、设销售这种商品每天所获得的利润为W元,求W与x之间的函数表达式;该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?23. (1)、【问题初探】如图1,E是正方形的边上一点,延长至点F,使 , 连接 , .求证:.(2)、【问题再探】如图2,E,M分别是正方形的边 , 上一点,分别过点M,E作于点P,于点Q,线段 , 相交于点N.连接 , , , , 若.
(1)、【问题初探】如图1,E是正方形的边上一点,延长至点F,使 , 连接 , .求证:.(2)、【问题再探】如图2,E,M分别是正方形的边 , 上一点,分别过点M,E作于点P,于点Q,线段 , 相交于点N.连接 , , , , 若.①求证:.
②探究和的面积关系,并说明理由.
(3)、【问题延伸】如图3,在正方形中,E,M分别是射线 , 上一点,【问题再探】中的其余条件不变,请直接判断和的面积关系是否仍成立.24. 如图,内接于 , , 点D为劣弧上动点,延长AD,BC交于点E,作交于F,连结.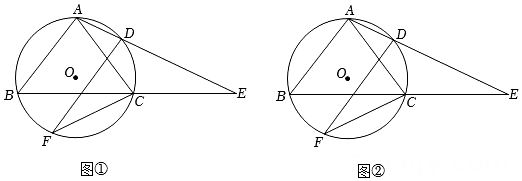 (1)、如图①,当点D为的中点时,求证:;(2)、如图②,若 , , 请用含有的代数式表示;(3)、在(2)的条件下,若 ,
(1)、如图①,当点D为的中点时,求证:;(2)、如图②,若 , , 请用含有的代数式表示;(3)、在(2)的条件下,若 ,①求证:;
②求的值.