2022-2023年华师大版数学八年级下册期末试卷(一)
试卷更新日期:2023-04-25 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 要使代数式有意义,则的取值范围是( )A、 B、 C、 D、且2. 下列说法中,不正确的是( )A、平行四边形的对角线互相平分 B、平行四边形的对边相等 C、两组对边分别相等的四边形是平行四边形 D、对角线相等的四边形是平行四边形3. 如表记录了甲、乙、丙、丁四位选手各10次射击成绩的数据信息,请你根据表中数据选一人参加比赛,最合适的人选是( )
选手
甲
乙
丙
丁
平均数(环)
9.2
9.3
9.3
9.2
方差(环2)
0.035
0.015
0.035
0.015
A、甲 B、乙 C、丙 D、丁4. 复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0).学生们在独立思考后,给出了5条关于这个函数的结论:①此函数是一次函数,但不可能是正比例函数;
②函数的值y 随着自变量x的增大而减小;
③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3、y轴围成的面积必小于0.5.
对于以上5个结论是正确有( )个.
A、4 B、3 C、2 D、05. 已知4个正数a1 , a2 , a3 , a4的平均数是a , 且a1>a2>a3>a4 , 则数据a1 , a2 , 0,a3 , a4的平均数和中位数是( )A、 a , a2 B、 a , a3 C、a , 0 D、a , a36. 如图,在平行四边形ABCD中,AD=2,AB= ,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF、EF.若∠EFD=90°,则AE长为( ) A、2 B、 C、 D、7. 若关于x的分式方程无解,则a的值为( )A、1 B、-1 C、1或0 D、1或-18. 如图,直线y=x+m与y=nx﹣5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx﹣5n>0的整数解为( )
A、2 B、 C、 D、7. 若关于x的分式方程无解,则a的值为( )A、1 B、-1 C、1或0 D、1或-18. 如图,直线y=x+m与y=nx﹣5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx﹣5n>0的整数解为( )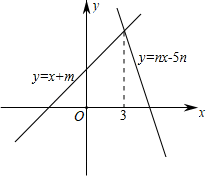 A、3 B、4 C、5 D、69. 如图,在平面直角坐标系中,一次函数 的图象分别交 轴于点 ,直线 与 轴交于点 ,若 ,则直线 的函数表达式是( )
A、3 B、4 C、5 D、69. 如图,在平面直角坐标系中,一次函数 的图象分别交 轴于点 ,直线 与 轴交于点 ,若 ,则直线 的函数表达式是( ) A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=6,BC=8,M是AD上任意一点,且ME⊥AC于点E,MF⊥BD于点F,则ME+MF为( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=6,BC=8,M是AD上任意一点,且ME⊥AC于点E,MF⊥BD于点F,则ME+MF为( ) A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题(每空3分,共15分)
-
11. 若 的值为 ,则 的值为.12. 若分式 的值为零,则x的值为 .13. 如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=6,则GH的最小值是 .
 14. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差s2:
14. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差s2:甲
乙
丙
丁
平均数 (cm)
561
560
561
560
方差s2(cm2)
3.5
3.5
15.5
16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择 .
15. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .
三、解答题(共8题,共75分)
-
16. 先化简,再求值: , 其中17.
某农场学校积极开展阳光体育活动,组织了八年级学生定点投篮,规定每人投篮3次.现对八年级(5)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
(1)求出八年级(5)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若八年级有学生200人,估计投中次数在2次以上(包括2次)的人数. 18. 如图,正方形和正方形有公共点A,点B在线段上.判断与的位置关系,并说明理由;
18. 如图,正方形和正方形有公共点A,点B在线段上.判断与的位置关系,并说明理由; 19. 某文体店在开学来临之际购进A,B两类足球销售,已知每个A类足球的进价比B类足球的进价高元,用元购进的A类足球和用元购进的B类足球数量相等.(1)、求每个A类足球和B类足球的进价分别是多少元?(2)、该商店计划用元购进一批A类足球和B类足球,该文体店A类足球每个售价为元,B类足球每个售价元,设销售总利润为W元,若要求购进的A类足球数量不少于B类足球数量,问如何进货可使总利润W最大.20. 如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.求证:四边形ABEF是菱形;
19. 某文体店在开学来临之际购进A,B两类足球销售,已知每个A类足球的进价比B类足球的进价高元,用元购进的A类足球和用元购进的B类足球数量相等.(1)、求每个A类足球和B类足球的进价分别是多少元?(2)、该商店计划用元购进一批A类足球和B类足球,该文体店A类足球每个售价为元,B类足球每个售价元,设销售总利润为W元,若要求购进的A类足球数量不少于B类足球数量,问如何进货可使总利润W最大.20. 如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.求证:四边形ABEF是菱形;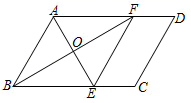 21. 如图,在四边形中, , 对角线交于点O,平分 .
21. 如图,在四边形中, , 对角线交于点O,平分 . (1)、求证:四边形是菱形;(2)、过点D作 , 交的延长线于点E,连接 , 若 , 求菱形的边长.22. 如图,在平面直角坐标系中,一次函数的图像与x轴交于点 , 与y轴交于点B,且与正比例函数的图像交点为 .
(1)、求证:四边形是菱形;(2)、过点D作 , 交的延长线于点E,连接 , 若 , 求菱形的边长.22. 如图,在平面直角坐标系中,一次函数的图像与x轴交于点 , 与y轴交于点B,且与正比例函数的图像交点为 . (1)、求a的值与一次函数的解析式;(2)、求的面积;(3)、若在x轴上存在一点P使为等腰三角形,请直接写出所有符合条件的点P的坐标.23. 如图,点A的坐标为 , , 点C从点A出发沿AB方向以每秒4个单位长度的速度向点B匀速运动,同时点D从点O出发沿OA方向以每秒2个单位长度的速度向点A匀速运动,设点C、D运动的时间是t秒().过点C作于点E,连接CD,DE.
(1)、求a的值与一次函数的解析式;(2)、求的面积;(3)、若在x轴上存在一点P使为等腰三角形,请直接写出所有符合条件的点P的坐标.23. 如图,点A的坐标为 , , 点C从点A出发沿AB方向以每秒4个单位长度的速度向点B匀速运动,同时点D从点O出发沿OA方向以每秒2个单位长度的速度向点A匀速运动,设点C、D运动的时间是t秒().过点C作于点E,连接CD,DE. (1)、求直线AB的解析式;(2)、求证:四边形ACED是平行四边形;(3)、当t为何值时,四边形CEOD的矩形?请直接写出t的值.
(1)、求直线AB的解析式;(2)、求证:四边形ACED是平行四边形;(3)、当t为何值时,四边形CEOD的矩形?请直接写出t的值.