青海省2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 每年秋季开学,学校组织同学们进行视力测试,如图是视力表的一部分,其中开口向上的两个“”之间的变换是( )
 A、平移 B、对称 C、位似 D、旋转2. 一只蚂蚁趴在如图所示的数轴上,它从点A沿数轴向右爬行2个单位长度到达点B,设点A表示 , 那么点B所表示的数为( )
A、平移 B、对称 C、位似 D、旋转2. 一只蚂蚁趴在如图所示的数轴上,它从点A沿数轴向右爬行2个单位长度到达点B,设点A表示 , 那么点B所表示的数为( ) A、 B、 C、 D、3. 如图,线段在第二象限,点 , 点 . 将线段绕点顺时针旋转得到线段 . 那么点的对应点的坐标是( )
A、 B、 C、 D、3. 如图,线段在第二象限,点 , 点 . 将线段绕点顺时针旋转得到线段 . 那么点的对应点的坐标是( ) A、 B、 C、 D、4. 估计 +1的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间5. 为响应“科教兴国”的战略号召,某学校计划成立创客实验室,现需购买航拍无人机和编程机器人.已知购买2架航拍无人机和3个编程机器人所需费用相同,购买4个航拍无人机和7个编程机器人共需34800元,设购买1架航拍无人机需x元,购买1个编程机器人需y元,则可列方程组为( )A、 B、 C、 D、6. 在中,是边的中点,若 , , 则的中线长的取值范围是( )A、 B、 C、 D、7. 如图,这是一个带“矮”圆柱形底的半球形的碗,则该几何体的俯视图是( )
A、 B、 C、 D、4. 估计 +1的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间5. 为响应“科教兴国”的战略号召,某学校计划成立创客实验室,现需购买航拍无人机和编程机器人.已知购买2架航拍无人机和3个编程机器人所需费用相同,购买4个航拍无人机和7个编程机器人共需34800元,设购买1架航拍无人机需x元,购买1个编程机器人需y元,则可列方程组为( )A、 B、 C、 D、6. 在中,是边的中点,若 , , 则的中线长的取值范围是( )A、 B、 C、 D、7. 如图,这是一个带“矮”圆柱形底的半球形的碗,则该几何体的俯视图是( )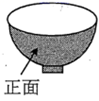 A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,是由两个大小完全相同的圆柱形容器在中间连通而成的可以盛水的器具,现匀速地向容器A中注水,则容器A中水面上升的高度h随时间t变化的大致图象是( )
8. 如图,是由两个大小完全相同的圆柱形容器在中间连通而成的可以盛水的器具,现匀速地向容器A中注水,则容器A中水面上升的高度h随时间t变化的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 分解因式: .10. 中国北斗卫星导航系统(BDS)是我国自行研制的全球卫星导航系统.北导航系统可在全球范围内全天候为各类用户提供高精度、高可靠定位、导航、授时服务,定位精度10米,测速精度0.2米秒,授时精度 秒.数字 用科学记数法表示为.11. 在一次体育达标测试中,某小组6名学生的立定跳远成绩如下:9, , 6,6,8,4.其中这组数据的众数是6和8,则这组数据的中位数是 .12. 如图,在中,是的平分线,是的平分线,与相交于点 , 若 , 则的度数是 .
 13. 如图,在中,延长至 , 使得 , 过中点作(点位于点右侧),且 , 连接 . 若 , 则的长为 .
13. 如图,在中,延长至 , 使得 , 过中点作(点位于点右侧),且 , 连接 . 若 , 则的长为 . 14. 如图,已知:⊙O与△ABC的边AB,AC,BC分别相切于点D,E,F,若AB=4,AC=5,AD=1,则BC= .
14. 如图,已知:⊙O与△ABC的边AB,AC,BC分别相切于点D,E,F,若AB=4,AC=5,AD=1,则BC= . 15. 某市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60 cm,水面至管道顶的距离为10 cm,则修理人员准备更换的新管道的内径为 .
15. 某市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60 cm,水面至管道顶的距离为10 cm,则修理人员准备更换的新管道的内径为 . 16. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,乙烯的化学式是 , 丙稀的化学式是…,碳原子和氢原子的数目满足一定数学规律.设碳原子的数目为n(n为正整数,且n≥2),则这类稀的化学式可用式子来表示.
16. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,乙烯的化学式是 , 丙稀的化学式是…,碳原子和氢原子的数目满足一定数学规律.设碳原子的数目为n(n为正整数,且n≥2),则这类稀的化学式可用式子来表示.三、解答题
-
17. 解不等式组 请按下列步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:(4)、原不等式组的解集为:18. 先化简,再求值: , 其中 , .19. 如图,一次函数y=mx+n(m≠0)的图象与反比例函数 (k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,已知△AOC的面积为4.
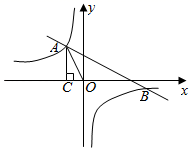 (1)、分别求出a和b的值.(2)、结合图象直接写出 中x的取值范围.20. 如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)、分别求出a和b的值.(2)、结合图象直接写出 中x的取值范围.20. 如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.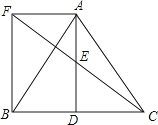 (1)、求证:D是BC的中点;(2)、若AB=AC,试判断四边形AFBD的形状,并证明你的结论.21. 如图,在航线的两侧分别有观测点和 , 点到航线的距离为2 , 点B位于点北偏东方向且与相距10处.现有一艘轮船从位于点南偏西方向的处,正沿该航线自西向东航行,5后该轮船行至点的正北方向的处.
(1)、求证:D是BC的中点;(2)、若AB=AC,试判断四边形AFBD的形状,并证明你的结论.21. 如图,在航线的两侧分别有观测点和 , 点到航线的距离为2 , 点B位于点北偏东方向且与相距10处.现有一艘轮船从位于点南偏西方向的处,正沿该航线自西向东航行,5后该轮船行至点的正北方向的处. (1)、求观测点到航线的距离;(2)、求该轮船航行的距离的长(结果精确到0.1).(参考数据: , , , )22. 为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现在随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果绘制了如下两幅不完整的统计图.
(1)、求观测点到航线的距离;(2)、求该轮船航行的距离的长(结果精确到0.1).(参考数据: , , , )22. 为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现在随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果绘制了如下两幅不完整的统计图.
请根据图中信息回答下列问题:
(1)、本次调查的样本容量是;(2)、补全条形统计图:(3)、若该学校共有3600名学生,试估计该校最想去森林公园的学生人数;(4)、从选项为“D(森林公园)”的学生中抽取了小明和小军两人做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁选择的数,谁就获胜;若小军选择的数是5,用列表或画树状图的方法求他获胜的概率. 23. 如图,是的直径,与相切于点 , 过点作交于点 , 连接 , 交于点 .
23. 如图,是的直径,与相切于点 , 过点作交于点 , 连接 , 交于点 .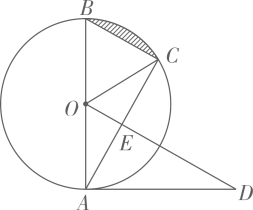 (1)、求证:;(2)、若 , , 求图中阴影部分的面积.24. 提出问题
(1)、求证:;(2)、若 , , 求图中阴影部分的面积.24. 提出问题为解方程 , 我们可以将视为一个整体,然后可设 , 则 , 于是原方程可转化为 , 解此方程,得 , .
当时, , , ∴;
当时, , , ∴ .
∴原方程的解为 , , , .
以上方法就是换元法解方程,从而达到了降次的目的,体现了转化的思想.
解决问题
(1)、运用上述换元法解方程 .(2)、已知实数m,n满足 , 求的值.25. 如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法: , 即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)、求抛物线和直线AB的解析式;(2)、点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及; (3)、是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
(3)、是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.