内蒙古呼和浩特2023年九年级中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下列图标中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,数轴上点A所表示的数的相反数为( )
2. 如图,数轴上点A所表示的数的相反数为( )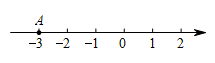 A、-3 B、3 C、 D、3. 用代入法解一元二次方程过程中,下列变形错误的是( )A、由①得 B、由①得 C、由②得 D、由②得4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是某企业2020年5~10月份月利润变化情况的折线统计图,下列说法与图中反映的信息相符的是( )
A、-3 B、3 C、 D、3. 用代入法解一元二次方程过程中,下列变形错误的是( )A、由①得 B、由①得 C、由②得 D、由②得4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是某企业2020年5~10月份月利润变化情况的折线统计图,下列说法与图中反映的信息相符的是( )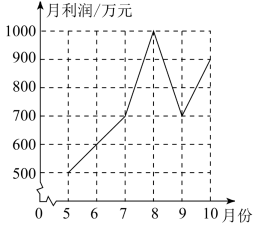 A、5~6月份月利润增长量大于9~10月份月利润增长量 B、5~10月份月利润的中位数是700万元 C、5~10月份月利润的平均数是760万元 D、5~10月份月利润的众数是1000万元6. 下列命题:(1)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍(2)相等的圆心角所对的弦相等(3)对角线相等且互相垂直的四边形是正方形(4)经过直线外一点有且只有一条直线与这条直线平行,其中真命题的个数有( )A、4个 B、3个 C、2个 D、1个7. 如图,在中, , . 将绕点按顺时针方向旋转至的位置时,点恰好落在边的中点处,则的长为( )
A、5~6月份月利润增长量大于9~10月份月利润增长量 B、5~10月份月利润的中位数是700万元 C、5~10月份月利润的平均数是760万元 D、5~10月份月利润的众数是1000万元6. 下列命题:(1)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍(2)相等的圆心角所对的弦相等(3)对角线相等且互相垂直的四边形是正方形(4)经过直线外一点有且只有一条直线与这条直线平行,其中真命题的个数有( )A、4个 B、3个 C、2个 D、1个7. 如图,在中, , . 将绕点按顺时针方向旋转至的位置时,点恰好落在边的中点处,则的长为( ) A、1 B、 C、2 D、8. 2022年4月16日,神舟十三号载人飞船返回舱成功着陆,三名航天员平安归来,神舟十三号任务取得圆满成功.某航模店购进了“神舟”和“天宫”两款航空模型.已知每个“神舟”模型比“天宫”模型的进价多10元,且同样花费100元,购进“天宫”模型的数量比“神舟”模型多5个.设“天宫”模型进价为每个元,则下列方程正确的是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线交轴于点,交轴于点,以为边在第一象限作正方形 , 其中顶点恰好落在双曲线上,现将正方形沿轴向下平移个单位,可以使得顶点落在双曲线上,则的值为( )
A、1 B、 C、2 D、8. 2022年4月16日,神舟十三号载人飞船返回舱成功着陆,三名航天员平安归来,神舟十三号任务取得圆满成功.某航模店购进了“神舟”和“天宫”两款航空模型.已知每个“神舟”模型比“天宫”模型的进价多10元,且同样花费100元,购进“天宫”模型的数量比“神舟”模型多5个.设“天宫”模型进价为每个元,则下列方程正确的是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线交轴于点,交轴于点,以为边在第一象限作正方形 , 其中顶点恰好落在双曲线上,现将正方形沿轴向下平移个单位,可以使得顶点落在双曲线上,则的值为( ) A、 B、 C、2 D、10. 如图,在中, , 于点 . 点是上两点,且 , , 若 , . 则的值为( )
A、 B、 C、2 D、10. 如图,在中, , 于点 . 点是上两点,且 , , 若 , . 则的值为( )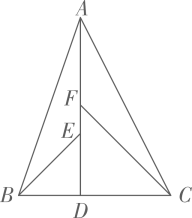 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解:= .12. 如图是某立体图形的三视图,该立体图形的名称是 , 若主视图和左视图均为边长为的等边三角形,则该立体图形的表面积为 .


 13. 盒子里装有若干个彩色球,它们除颜色外完全相同,其中有6个黄球,从盒子中任意摸出一个球,摸到黄球的概率是 , 则盒子里共有个彩色球.14. 如图是一个隧道的横截面,它的形状是以点为圆心的圆的一部分.如果是中弦的中点,经过圆心交于点 , 并且 , . 则的半径为 .
13. 盒子里装有若干个彩色球,它们除颜色外完全相同,其中有6个黄球,从盒子中任意摸出一个球,摸到黄球的概率是 , 则盒子里共有个彩色球.14. 如图是一个隧道的横截面,它的形状是以点为圆心的圆的一部分.如果是中弦的中点,经过圆心交于点 , 并且 , . 则的半径为 . 15. 如图在菱形中,为对角线与的交点,点为边上的任一点(不与、重合),过点分别作 , , 、为垂足,则可以判断四边形的形状为 . 若菱形的边长为 , , 则的最小值为 . (用含的式子表示)
15. 如图在菱形中,为对角线与的交点,点为边上的任一点(不与、重合),过点分别作 , , 、为垂足,则可以判断四边形的形状为 . 若菱形的边长为 , , 则的最小值为 . (用含的式子表示) 16. 新定义:在平面直角坐标系中,对于点和点 , 若满足时,;时, , 则称点是点的限变点.例如:点的限变点是 , 则点的限变点是 . 若点在二次函数的图象上,则当时,其限变点的纵坐标的取值范围是 .
16. 新定义:在平面直角坐标系中,对于点和点 , 若满足时,;时, , 则称点是点的限变点.例如:点的限变点是 , 则点的限变点是 . 若点在二次函数的图象上,则当时,其限变点的纵坐标的取值范围是 .三、解答题
-
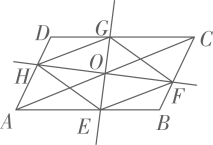
17. 计算求解(1)、计算:;(2)、先化简,再求值: , 其中 .18. 如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
 19. 某校为落实“双减”政策,增强课后服务的丰富性,充分用好课后服务时间,3月份学校开展数学学科活动,其中七年级开展了五个项目(每位学生只能参加一个项目):A.阅读数学名著;B.讲述数学故事;C.制作数学模型;D.参与数学游戏;E.挑战数学竞赛.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
19. 某校为落实“双减”政策,增强课后服务的丰富性,充分用好课后服务时间,3月份学校开展数学学科活动,其中七年级开展了五个项目(每位学生只能参加一个项目):A.阅读数学名著;B.讲述数学故事;C.制作数学模型;D.参与数学游戏;E.挑战数学竞赛.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)、①此次调查一共随机抽取了 ▲ 名学生;②补全条形统计图(要求在条形图上方注明名数);
③扇形统计图中圆心角 ▲ 度;
(2)、若该年级有1100名学生,请你估计该年级参加D项目的学生大约有多少名;(3)、在C项目展示活动中,某班获得一等奖的学生有3名男生,2名女生,则从这5名学生中随机抽取2名学生代表本班参加学校制作数学模型活动,请直接写出恰好抽到2名男生的概率.20. 如图,某测量小组为了测量山的高度,在地面处测得山顶的仰角 , 然后沿着坡角为(即)的坡面走了200米到达处,此时在处测得山顶的仰角为 , 求山高(结果保留根号)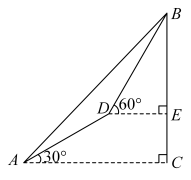 21. 如图,点 , 是反比例函数图像上的两点,过点 , 分别作轴于点 , 轴于点 , 连接 , 已知点 , , ,
21. 如图,点 , 是反比例函数图像上的两点,过点 , 分别作轴于点 , 轴于点 , 连接 , 已知点 , , , (1)、求点坐标及反比例函数解析式;(2)、若所在直线的解析式为 , 根据图像,请直接写出不等式的解集.22. 某校九年级学生小丽、小强和小红到某商场参加了社会实践活动,在活动中他们参与了某商品的销售工作,已知该商品的进价为40元/件,售价为60元/件,下面是他们在活动结束后的对话:
(1)、求点坐标及反比例函数解析式;(2)、若所在直线的解析式为 , 根据图像,请直接写出不等式的解集.22. 某校九年级学生小丽、小强和小红到某商场参加了社会实践活动,在活动中他们参与了某商品的销售工作,已知该商品的进价为40元/件,售价为60元/件,下面是他们在活动结束后的对话:小丽:我发现此商品如果按60元/件销售,每星期可卖出件.
小强:我发现在售价60元/件的基础上调整价格,每涨价元,每星期比小丽所调查的销售量300件要少卖出10件.
小红:我发现在售价60元/件的基础上调整价格,每降价元,每星期比小丽所调查的销售量300件要多卖出20件.
(1)、若设每件涨价元,则每星期实际可卖出件,每星期售出商品的利润(元)与的关系式为 , 的取值范围是 .(2)、若设每件降价元,则每星期售出商品的利润(元)与的关系式为 .(3)、在涨价情况下,如何定价才能使每星期售出商品的利润最大?最大利润是多少?
