内蒙古包头市青原区2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下列计算 的结果中,正确的是( )A、 B、 C、 D、
-
2. 如图是由若干个小正方体堆成的几何体的主视图(正视图),这个几何体是( )
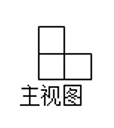 A、
A、 B、
B、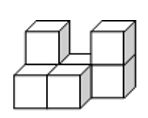 C、
C、 D、
D、
-
3. 有理数a,b在数轴上的对应点的位置如图所示,则下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4. 下列变形中正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得
-
5. 学校开展“书香校园,师生共读”活动,某学习小组五名同学一周的课外阅读时间(单位:),分别为:4,5,5,6,10.这组数据的平均数、方差是( )A、6,4.4 B、5,6 C、6,4.2 D、6,5
-
6. 一次动员会上,为了鼓励运动员奋力拼搏,某班级将分别标有“你”“我”“加”“油”汉字的四张卡片装在一个不透明的口袋中,这些卡片除汉字外无其他差别,每次摸卡片前先搅拌均匀随机摸出一张,不放回;再随机摸出一张卡片,两次摸出的卡片上的汉字可以组成“加油”的概率是( )A、 B、 C、 D、
-
7. 如图,是的直径,C、D是上的点, , 过点C作的切线交的延长线于点E,则等于( )
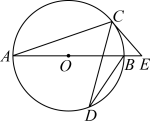 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 若关于x的方程+=3的解是非负数,则m的取值范围为( )A、m≤-7且m≠-3 B、m≥-7且m≠-3 C、m≤-7 D、m≥-7
-
9. 如图中, , 若将作点逆时针旋转 , 得到 , 连接 , 则在点运动过程中,线段的最小值为( )
 A、2 B、 C、 D、1
A、2 B、 C、 D、1 -
10. 如图,在同一直角坐标系中,函数y= 与y=kx+k2的大致图象是( )A、
 B、
B、 C、
C、 D、
D、
-
11. 如图,抛物线y=ax2+bx+c的顶点坐标为(1,n).下列结论:①abc<0;②8a+c<0;③关于x的一元二次方程ax2+bx+c=n-1有两个不相等实数根;④抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2 . 其中正确的结论共有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
12. 如图,正方形边长为 , 为边上一点, , 连接 , 过A作 , 交的延长线于点 , 连接 , 过A作 , 垂足为点 , 连接则线段的长为( )
 A、3 B、 C、 D、
A、3 B、 C、 D、
二、填空题
-
13. 如图,故宫又称紫禁城,位于北京中轴线的中心,占地面积约 , 在世界宫殿建筑群中面积最大.将720000用科学记数法表示为 .

-
14. 代数式有意义,则的取值范围是 .
-
15. 若某正数的两个平方根分别是与 , 则b的立方根是 .
-
16. 已知 , 则的值为 .
-
17. 已知多项式 , 且的值与字母x的取值无关,则的值为 .
-
18. 如图,四边形ABCD和CEFG是两个相邻的正方形,其中B,C,E在同一条直线上,点D在CG上,它们的面积分别为27平方米和48平方米,则BE的长为米.

-
19. 如图,是半圆的直径, , 是半圆弧的三等分点,于点 , 连接 , 若 , 则图中阴影部分的面积为 .

-
20. 在直角坐标系中,等腰直角三角形按如图所示的方式放置,其中点均在一次函数的图象上,点均在x轴上.若点的坐标为 , 点的坐标为 , 则点的坐标为 .

三、解答题
-
21. 某校对九年级学生进行了一次防疫知识竞赛,并随机抽取甲、乙两班各50名学生的竞赛成绩(满分100分)进行整理,描述分析.下面给出部分信息:甲班成绩的频数分布直方图如图所示(数据分为6组: , , , , , ),其中90分以及90分以上的人为优秀;甲班的成绩在这一组的是:72,72,73,75,76,77,77,78,78,79,79,79,79.甲、乙两班成级的平均数、中位数、众数和优秀人数如下表:
平均数
中位数
众数
优秀人数
甲班成绩
78
m
85
3
乙班成绩
75
73
82
6

根据以上信息,回答下列问题:
(1)、表中的;(2)、在此次竞赛中,你认为甲班和乙班中,班表现的更优异,理由是;(3)、如果该校九年级学生有600名,估计九年级学生成绩优秀的有多少人? -
22. 如图①是一台手机支架,图②是其侧面示意图,、可分别绕点、转动,测量知 , . 当 , 转动到 , 时,求点到直线的距离.(精确到 , 参考数据: , , )
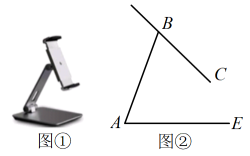
-
23. 某批发市场批发甲、乙两种水果,甲种水果的销售利润(万元)与进货量(吨)近似满足函数关系;乙种水果的销售利润(万元)与进货量(吨)近似满足函数关系(其中 , , 为常数),且进货量为1吨时,销售利润为1.4万元;进货量为3吨时,销售利润为3.6万元.(1)、求(万元)与(吨)之间的函数关系式;(2)、如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为吨,销售完毕,这两种水果所获最大利润是多少?
-
24. 如图,是的直径,为上一点,为外一点,连接 , , , , 满足 , .
 (1)、证明:直线为的切线;(2)、射线与射线交于点 , 若 , , 求的长.
(1)、证明:直线为的切线;(2)、射线与射线交于点 , 若 , , 求的长. -
25. 在平面直角坐标系中,抛物线与x轴交于点A和点B,与y轴交于点C,点B坐标为 , 点D坐标为 , 点P为第一象限内抛物线上一点.
 (1)、b的值为;(2)、如图1,连接 , , 设与交于点E,若 , 求点E坐标;(3)、如图2,设直线与线段所夹锐角为 , 若 , 求点P的坐标.
(1)、b的值为;(2)、如图1,连接 , , 设与交于点E,若 , 求点E坐标;(3)、如图2,设直线与线段所夹锐角为 , 若 , 求点P的坐标. -
26.(1)、问题提出
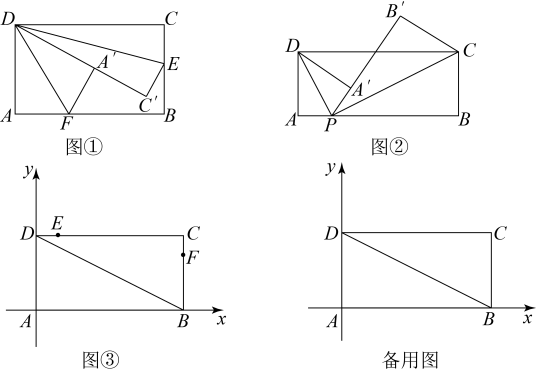
如图①,在矩形的边上找一点E,将矩形沿直线折叠,点C的对应点为 , 再在上找一点F,将矩形沿直线折叠,使点A的对应点落在上则 .
(2)、问题探究如图②在矩形中, , , 点P是矩形边上一点,连接 , 将、分别沿翻折,得到、 , 当P、、三点共线时,则称P为边上的“优叠点”,求此时的长度.
(3)、问题解决如图③,矩形位于平面直角坐标系中, , . 点A在标原点,B,D分别在x轴与y轴上,点E和点F分别是和边上的动点,运动过程中始终保持 . 当点P是边上唯一的“优叠点”时,连接交于点M,连接交于点N,请问是否能取得最大值?如果能,请确定此时点M的位置(即求出点M的坐标)及四边形的面积,若不能,请说明理由.
