辽宁省辽阳市灯塔市2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下列各数是负数的是( )A、 B、 C、 D、2. 如图是《九章算术》中“堑堵”的立体图形,它的左视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 剪纸是中国民间艺术的瑰宝,下列剪纸作品中既是轴对称图形,又是中心对称图形的是( )A、
3. 下列计算正确的是( )A、 B、 C、 D、4. 剪纸是中国民间艺术的瑰宝,下列剪纸作品中既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 为了改善生态环境,某社区计划在荒坡上种植600棵树,由于学生志愿者的加入,每日比原计划多种20%,结果提前1天完成任务.设原计划每天种树x棵,可列方程( )A、 B、 C、 D、6. 某校积极鼓励学生参加志愿者活动,下表列出了随机抽取的名学生一周参与志愿者活动的时间情况:
5. 为了改善生态环境,某社区计划在荒坡上种植600棵树,由于学生志愿者的加入,每日比原计划多种20%,结果提前1天完成任务.设原计划每天种树x棵,可列方程( )A、 B、 C、 D、6. 某校积极鼓励学生参加志愿者活动,下表列出了随机抽取的名学生一周参与志愿者活动的时间情况:参与志愿者活动的时间(h)
1
2
3
参与志愿者活动的人数(人)
x
8
2
根据表中数据,下列说法中错误的是( )
A、表中的值为 B、这组数据的众数是 C、这组数据的中位数是 D、这组数据的平均数是7. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若 , , 则菱形ABCD的边长为( ) A、2 B、2.5 C、3 D、58. 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A、2 B、2.5 C、3 D、58. 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( ) A、4 B、8 C、6 D、109. 如图,二次函数的图象与x轴相交于 , B两点,对称轴是直线 , 下列说法正确的是( )
A、4 B、8 C、6 D、109. 如图,二次函数的图象与x轴相交于 , B两点,对称轴是直线 , 下列说法正确的是( )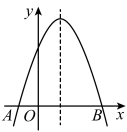 A、 B、当时,y的值随x值的增大而增大 C、点B的坐标为 D、10. 如图,在中, , , , 是边上的中线,将沿射线方向以每秒个单位长度的速度平移,平移后的三角形记为 , 设与重叠部分的面积为 , 平移运动时间为 , 当点与点重合时,停止运动,则下列图象能反映与之间函数关系的是( )
A、 B、当时,y的值随x值的增大而增大 C、点B的坐标为 D、10. 如图,在中, , , , 是边上的中线,将沿射线方向以每秒个单位长度的速度平移,平移后的三角形记为 , 设与重叠部分的面积为 , 平移运动时间为 , 当点与点重合时,停止运动,则下列图象能反映与之间函数关系的是( )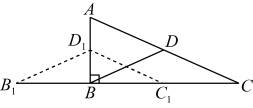 A、
A、 B、
B、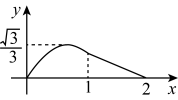 C、
C、 D、
D、
二、填空题
-
11. 《全国防沙治沙规划(年》》正式印发实施,提出到2030年,规划完成沙化土地治理任务1.86亿亩.数据“1.86亿”用科学记数法表示为 .12. 如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E=.
 13. 已知关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是 .14. 若方程组 的解满足 ,则a=.15. 如图是甲、乙两人5次投篮成绩统计图(每人每次投球10个),则 (填“>”,“=”或“<”).
13. 已知关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是 .14. 若方程组 的解满足 ,则a=.15. 如图是甲、乙两人5次投篮成绩统计图(每人每次投球10个),则 (填“>”,“=”或“<”). 16. 如图,在平面直角坐标系中,点为第一象限内一点,且.连接 , 并以点为旋转中心把逆时针转90°后得线段.若点恰好都在同一反比例函数的图象上,则的值等于.
16. 如图,在平面直角坐标系中,点为第一象限内一点,且.连接 , 并以点为旋转中心把逆时针转90°后得线段.若点恰好都在同一反比例函数的图象上,则的值等于. 17. 如图,是的直径, , 两点在圆上,连接 , , 且 , , 为上一动点,在运动过程中,与相交于点 , 当为等腰三角形时,的度数为 .
17. 如图,是的直径, , 两点在圆上,连接 , , 且 , , 为上一动点,在运动过程中,与相交于点 , 当为等腰三角形时,的度数为 . 18. 如图,正方形ABCD的边长为4,P是边CD上的一动点,EF⊥BP交BP于G,且EF平分正方形ABCD的面积,则线段GC的最小值是.
18. 如图,正方形ABCD的边长为4,P是边CD上的一动点,EF⊥BP交BP于G,且EF平分正方形ABCD的面积,则线段GC的最小值是.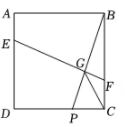
三、解答题
-
19. 先化简,再求值: ,其中x为不等式组 的整数解.20. 某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:
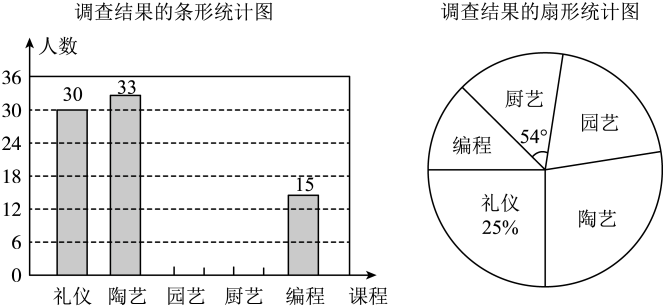
请结合上述信息,解答下列问题:
(1)、共有名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是度;(2)、补全调查结果条形统计图;(3)、小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.21. 建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?22. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线.为了测量房屋的高度,在地面上点测得屋顶的仰角为 , 此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走8m到达点时,又测得屋檐点的仰角为 , 房屋的顶层横梁 , , 交于点(点 , , 在同一水平线上).(参考数据: , , , , , )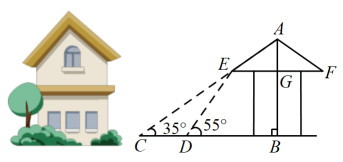 (1)、求屋顶到横梁的距离;(2)、求房屋的高 .23. 我市某景区商店在销售北京冬奥会吉祥物“冰墩墩”纪念品时,发现该纪念品的月销售量y件是销售单价x元的一次函数,如表是该商品的销售数据.
(1)、求屋顶到横梁的距离;(2)、求房屋的高 .23. 我市某景区商店在销售北京冬奥会吉祥物“冰墩墩”纪念品时,发现该纪念品的月销售量y件是销售单价x元的一次函数,如表是该商品的销售数据.销售单价x(元)
40
50
月销售量y(件)
100
80
(1)、求y与x的函数关系式;(2)、若该商品的进货单价是30元.请问,每件商品的销售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?24. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD. (1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.25. 在中, , , 是的角平分线,于点 .
(1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.25. 在中, , , 是的角平分线,于点 . (1)、如图1,连接 , 求证:是等边三角形;(2)、点是线段上的一点(不与点 , 重合),以为一边,在的下方作 , 交延长线于点 . 请你在图2中画出完整图形,并直接写出 , 与之间的数量关系;(3)、如图3,点是线段上的一点,以为一边,在的下方作 , 交延长线于点 . 试探究 , 与数量之间的关系,并说明理由.26. 如图,在平而直角坐标系中,抛物线与x轴交于 , 两点,与y轴交于点C.
(1)、如图1,连接 , 求证:是等边三角形;(2)、点是线段上的一点(不与点 , 重合),以为一边,在的下方作 , 交延长线于点 . 请你在图2中画出完整图形,并直接写出 , 与之间的数量关系;(3)、如图3,点是线段上的一点,以为一边,在的下方作 , 交延长线于点 . 试探究 , 与数量之间的关系,并说明理由.26. 如图,在平而直角坐标系中,抛物线与x轴交于 , 两点,与y轴交于点C. (1)、试求抛物线的解析式;(2)、直线与y轴交于点D,与抛物线在第一象限交于点P,与直线交于点M,记 , 试求m的最大值及此时点P的坐标;(3)、在(2)的条件下,m取最大值时,是否存在x轴上的点Q及坐标平面内的点N,使得P,D,Q,N四点组成的四边形是矩形?若存在,请直接写出所有满足条件的Q点和N点的坐标:若不存在,请说明理由.
(1)、试求抛物线的解析式;(2)、直线与y轴交于点D,与抛物线在第一象限交于点P,与直线交于点M,记 , 试求m的最大值及此时点P的坐标;(3)、在(2)的条件下,m取最大值时,是否存在x轴上的点Q及坐标平面内的点N,使得P,D,Q,N四点组成的四边形是矩形?若存在,请直接写出所有满足条件的Q点和N点的坐标:若不存在,请说明理由.