江西省赣州市寻乌县2023年中考一模数学试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. -3的相反数是( )A、3 B、-3 C、0 D、±32. 下面的计算正确的是( )A、 B、 C、 D、3. 下列各图是选自历届世博会徽中的图案,其中是中心对称图形的是( )A、

B、
B、
C、
C、
D、
D、
4. 如下图所示的几何体,它的俯视图是( )
4. 如下图所示的几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,的半径弦于点C,连接并延长交于点E,连接 . 若 , , 则的长为( )
5. 如图,的半径弦于点C,连接并延长交于点E,连接 . 若 , , 则的长为( ) A、2 B、3 C、4 D、56. 已知二次函数的图象如图所示,下列四个命题:①;②;③若 , 是该抛物线上的两点,则;④若 , 是该抛物线上的两点,则;其中正确的结论有( )
A、2 B、3 C、4 D、56. 已知二次函数的图象如图所示,下列四个命题:①;②;③若 , 是该抛物线上的两点,则;④若 , 是该抛物线上的两点,则;其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 以抗美援朝战争为背景的爱国题材影片《长津湖》以约5746000000元的票房创造中国电影票房的新高,将5746000000用科学记数法表示为 .8. 分解因式: .
9. 设 , 是一元二次方程的两个根,则 .10. 幻方历史悠久,传说最早出现在夏禹时代的“洛书”当中,根据幻方的相等关系设计出来一个“幻圆”,即大圆.小圆.横线.竖线上的四个数字加起来的和均相等.如图给出了部分数字,则幻圆中的值为 . 11. 如图,将正方形纸板制成一个七巧板,拼成如图所示的“小鸟”图案,头部(阴影部分)的面积为 , 则“小鸟”图案中身体(空白部分)的面积为 .
11. 如图,将正方形纸板制成一个七巧板,拼成如图所示的“小鸟”图案,头部(阴影部分)的面积为 , 则“小鸟”图案中身体(空白部分)的面积为 .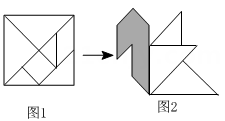 12. 如图,在矩形中, , , 点是的中点,点是边上一动点,将沿折叠,点的对应点为点 , 当射线经过矩形一边的中点时(不含点),则的长为 .
12. 如图,在矩形中, , , 点是的中点,点是边上一动点,将沿折叠,点的对应点为点 , 当射线经过矩形一边的中点时(不含点),则的长为 .
三、解答题
-
13.(1)、计算:(2)、解不等式组:14. 先化简,再求值: , 请在范围内选择一个你喜欢的整数代入求值.15. 如图,4张背面完全相同的纸牌(用①、②、③、④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机摸出一张(不放回),再随机摸出一张.
 (1)、用树状图(或列表法)表示两次摸牌出现的所有可能结果;(2)、以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率.16. 已知四边形ABCD内接于⊙O,且已知∠ADC=120°;请仅用无刻度直尺完成以下作图(保留作图痕迹,不写作法,写明答案).
(1)、用树状图(或列表法)表示两次摸牌出现的所有可能结果;(2)、以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率.16. 已知四边形ABCD内接于⊙O,且已知∠ADC=120°;请仅用无刻度直尺完成以下作图(保留作图痕迹,不写作法,写明答案). (1)、在图1中,已知AD=CD,在⊙O上求作一个度数为30°的圆周角;(2)、在图2中,已知AD≠CD,在⊙O上求作一个度数为30°的圆周角.17. 如图,在四边形中, , , 平分 , 连接交于点 , 过点作交延长线于点 .
(1)、在图1中,已知AD=CD,在⊙O上求作一个度数为30°的圆周角;(2)、在图2中,已知AD≠CD,在⊙O上求作一个度数为30°的圆周角.17. 如图,在四边形中, , , 平分 , 连接交于点 , 过点作交延长线于点 .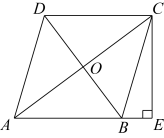 (1)、求证:四边形为菱形;(2)、若 , , 求的长.18. 为弘扬红色文化,传颂红色故事,赣南革命老区某学校特在九年级开展了红色文化知识竞赛活动,并随机抽取了20名参赛选手的成绩(竞赛成绩均为正数,满分100分)进行统计分析.随机抽取的成绩如下:
(1)、求证:四边形为菱形;(2)、若 , , 求的长.18. 为弘扬红色文化,传颂红色故事,赣南革命老区某学校特在九年级开展了红色文化知识竞赛活动,并随机抽取了20名参赛选手的成绩(竞赛成绩均为正数,满分100分)进行统计分析.随机抽取的成绩如下:77,86,80,76,70,100,95,80,75,90
94,86,68,95,88,78,90,82,86,100v
整理数据:
分数
人数
2
5
根据以上信息回答下列问题:
(1)、填空:a= , b=;(2)、这20名参赛人员成绩的众数为 , 中位数为;(3)、小李的参赛成绩为87分,你认为他的成绩属于“中上”水平吗?请说明理由.(4)、该学校九年级共有460名学生参加了竞赛,若成绩在90分(包含90分)以上为优秀,请你估计此次知识竞赛中优秀的人数.19. 如图,直线与轴,轴分别相交于 , 两点,与双曲线相交于点 , 轴于点 , 且 , 点的坐标为 . (1)、求一次函数和双曲线的解析式;(2)、若点为双曲线上点右侧的一点,且轴于 , 当时,求点的坐标.20. 脱贫攻坚工作让老百姓过上了幸福的生活;如图是政府给贫困户新建房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上点测得屋顶的仰角为 , 此时地面上点.屋檐上点.屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为 , 房屋的横梁 , , 交于点(点 , , 在同一水平线上).(参考数据: , , , )
(1)、求一次函数和双曲线的解析式;(2)、若点为双曲线上点右侧的一点,且轴于 , 当时,求点的坐标.20. 脱贫攻坚工作让老百姓过上了幸福的生活;如图是政府给贫困户新建房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上点测得屋顶的仰角为 , 此时地面上点.屋檐上点.屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为 , 房屋的横梁 , , 交于点(点 , , 在同一水平线上).(参考数据: , , , )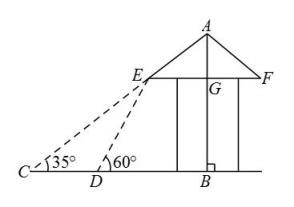 (1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到).21. 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到).21. 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB. (1)、求证:BC是⊙O的切线;(2)、连接AF,BF,求∠ABF的度数;(3)、如果CD=15,BE=10,sinA= , 求⊙O的半径.22. 【问题情境】
(1)、求证:BC是⊙O的切线;(2)、连接AF,BF,求∠ABF的度数;(3)、如果CD=15,BE=10,sinA= , 求⊙O的半径.22. 【问题情境】课外兴趣小组活动时,老师提出了如下问题:
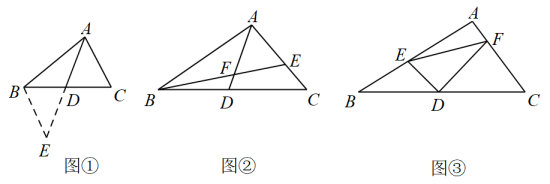
如图①,中,若 , , 求边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长至点 , 使 , 连接 .
请根据小明的方法思考:
(1)、由已知和作图能得到 , 依据是 .A.;B.;C.;D.
由“三角形的三边关系”可求得的取值范围是 .
(2)、【初步运用】如图②,是的中线,交于 , 交于 , 且 . 若 , , 求线段的长.
(3)、【灵活运用】如图③,在中, , 为中点, , 交于点 , 交于点 , 连接 . 试猜想线段 . . 三者之间的数量关系,并证明你的结论.
23. 定义:若直线与开口向下的抛物线有两个交点,则这两个交点之间的距离叫做这条抛物线的“反碟长”.如图,已知抛物线:与直线相交于 , . (1)、抛物线的“反碟长” .(2)、抛物线随其顶点沿直线向上平移,得到抛物线 .
(1)、抛物线的“反碟长” .(2)、抛物线随其顶点沿直线向上平移,得到抛物线 .①当抛物线的顶点平移到点 , 抛物线的解析式是 ▲ . 抛物线的“反碟长”是 ▲ .
②若抛物线的“反碟长”是一个偶数,则其顶点的纵坐标可能是 ▲ . (填写所有正确的选项)
A.15 B.16 C.24 D.25
③当抛物线的顶点和抛物线与直线的两个交点 , 构成一个等边三角形时(点在点左右),求点的坐标.