江苏省扬州市邗江区2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、-2023 B、2023 C、 D、2. 中国文字是方块字,其形、音、结构、神韵都具有美感,对称美在汉字结构中十分常见,下列美术字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 近期,扬州市统计局发布了《2022年扬州市国民经济和社会发展统计公报》,《公报》称,经初步核算,扬州市2022年房屋建筑施工面积约330100000平方米,同比增长1.5%,将330100000用科学记数法表示为( )A、 B、 C、 D、4. 如图是由5个完全相同的小正方形搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
3. 近期,扬州市统计局发布了《2022年扬州市国民经济和社会发展统计公报》,《公报》称,经初步核算,扬州市2022年房屋建筑施工面积约330100000平方米,同比增长1.5%,将330100000用科学记数法表示为( )A、 B、 C、 D、4. 如图是由5个完全相同的小正方形搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )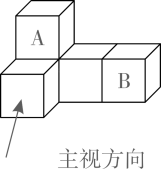 A、主视图会发生改变 B、俯视图会发生改变 C、左视图会发生改变 D、三种视图都会发生改变5. 中国古代数学著作《九章算术》第七章主要内容是“盈不足术”,其中有这样一道盈亏类问题:“今有共买羊,人出五,不足九十;人出五十,适足,问人数、羊价各几何?”题目大意是:“有几个人共同购买一只羊,若每人出五元,还差九十元;若每人出五十元,刚好够,问有几个人,羊的价格是多少?”设有人,羊的价格为元,可列方程组为( )A、 B、 C、 D、6. 下图中,图是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果,图是一个菱形,将图截去一个边长为原来一半的菱形得到图 , 用图镶嵌得到图 , 将图着色后,再次镶嵌便得到图 , 则图中的度数是( )
A、主视图会发生改变 B、俯视图会发生改变 C、左视图会发生改变 D、三种视图都会发生改变5. 中国古代数学著作《九章算术》第七章主要内容是“盈不足术”,其中有这样一道盈亏类问题:“今有共买羊,人出五,不足九十;人出五十,适足,问人数、羊价各几何?”题目大意是:“有几个人共同购买一只羊,若每人出五元,还差九十元;若每人出五十元,刚好够,问有几个人,羊的价格是多少?”设有人,羊的价格为元,可列方程组为( )A、 B、 C、 D、6. 下图中,图是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果,图是一个菱形,将图截去一个边长为原来一半的菱形得到图 , 用图镶嵌得到图 , 将图着色后,再次镶嵌便得到图 , 则图中的度数是( )
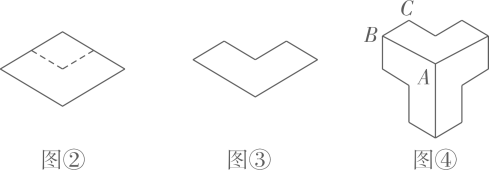 A、 B、 C、 D、7. 如图,直线经过点 , 当时,x的取值范围为( )
A、 B、 C、 D、7. 如图,直线经过点 , 当时,x的取值范围为( )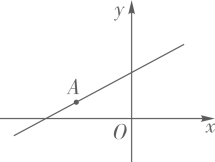 A、 B、 C、 D、8. 如图,在菱形纸片中, , E是边的中点,将菱形纸片沿过点A的直线折叠,使点B落在直线上的点G处,折痕为 , 与交于点H,有如下结论:①;②;③;④ , 上述结论中,所有正确结论的序号是( )
A、 B、 C、 D、8. 如图,在菱形纸片中, , E是边的中点,将菱形纸片沿过点A的直线折叠,使点B落在直线上的点G处,折痕为 , 与交于点H,有如下结论:①;②;③;④ , 上述结论中,所有正确结论的序号是( ) A、①②④ B、①②③ C、①③④ D、①②③④
A、①②④ B、①②③ C、①③④ D、①②③④二、填空题
-
9. 分解因式:.10. 在平面直角坐标系中,将点向右平移2个单位后,得到的点的坐标是 .11. 若关于x的方程的一个根为3,则m的值为 .12. 2023年3月7日上午,江苏省青少年射击(步手枪)冠军赛在扬州市射击运动中心鸣枪开赛.来自全省12个设区市的200余名青少年射击选手齐聚扬州,一较高下,赛前,某位射击运动员在训练中射击了10次,成绩如图所示,则该名选手十次射击训练成绩的中位数是 .
 13. 已知 , 则x的取值范围是 .14. 北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念,如图所示,它的主体形状呈正六边形,若点A,F,B,D,C,E是正六边形的六个顶点,则的值是 .
13. 已知 , 则x的取值范围是 .14. 北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念,如图所示,它的主体形状呈正六边形,若点A,F,B,D,C,E是正六边形的六个顶点,则的值是 . 15. 如图,等边三角形的边长为2,以B为圆心、长为半径画弧 , 点D为等边三角形内一点,连接若为等腰直角三角形,图中阴影部分的面积是 .
15. 如图,等边三角形的边长为2,以B为圆心、长为半径画弧 , 点D为等边三角形内一点,连接若为等腰直角三角形,图中阴影部分的面积是 . 16. 如图,正方形的顶点均在坐标轴上,且点的坐标为 , 以为边构造菱形 , 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2023次旋转结束时,点的对应点的坐标为 .
16. 如图,正方形的顶点均在坐标轴上,且点的坐标为 , 以为边构造菱形 , 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2023次旋转结束时,点的对应点的坐标为 . 17. 如图,A是双曲线()上的一点,M是线段上的点, , 过点M作x轴的垂线,垂足为B,交双曲线于点C,则的面积是 .
17. 如图,A是双曲线()上的一点,M是线段上的点, , 过点M作x轴的垂线,垂足为B,交双曲线于点C,则的面积是 . 18. 如图,在中,M,N分别为 , 上的点,将沿翻折,得到 , 连接 , , 已知 , 若 , , , 则的长为 .
18. 如图,在中,M,N分别为 , 上的点,将沿翻折,得到 , 连接 , , 已知 , 若 , , , 则的长为 .
三、解答题
-
19. 计算:(1)、;(2)、 .20. 解不等式组: , 并求出不等式组所有非正整数解的和.21. 2022年是我国航天事业辉煌的一年,神舟十四号和神舟十五号两个飞行乘组6位航天员在太空会师,在神州大地上掀起了航天热潮,某学校为了解本校学生对我国航天事业的了解情况,在全校范围内开展了航天知识竞赛,学校随机抽取了部分学生的成绩,整理并制成了如下不完整的频数分布表和频数分布直方图.
组号
成绩
频数
频率
1
3
0.06
2
a
0.24
3
20
0.40
4
b
c
5
5
合计
m
1.00
 (1)、本次抽样调查的样本容量;(2)、求表格中字母的值: ▲ , ▲ , ▲ , 并补全频数分布直方图;(3)、若以组中值(每组正中间数值)为本组数据的平均数,全校共有1000名学生参与竞赛,试估计所有参赛学生成绩的平均分.22. 勾股定理是人类早期发现并证明的重要数学定理之一,至今已有几百种证明方法,在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例;三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释并创制了一幅“勾股圆方图”;后刘徽用“出入相补”原理证明了勾股定理;清朝末年,数学家华蘅芳提出了二十多种对于勾股定理证法.(1)、某学校数学活动室进行文化建设,拟从以上4位科学家的画像中随机选用1幅,恰好选中的画像是刘徽的概率;
(1)、本次抽样调查的样本容量;(2)、求表格中字母的值: ▲ , ▲ , ▲ , 并补全频数分布直方图;(3)、若以组中值(每组正中间数值)为本组数据的平均数,全校共有1000名学生参与竞赛,试估计所有参赛学生成绩的平均分.22. 勾股定理是人类早期发现并证明的重要数学定理之一,至今已有几百种证明方法,在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例;三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释并创制了一幅“勾股圆方图”;后刘徽用“出入相补”原理证明了勾股定理;清朝末年,数学家华蘅芳提出了二十多种对于勾股定理证法.(1)、某学校数学活动室进行文化建设,拟从以上4位科学家的画像中随机选用1幅,恰好选中的画像是刘徽的概率;
 (2)、在某次数学活动中,有一个不透明的信封内装有三根长度分别为4cm,6cm和8cm的细木棒,木棒露出纸袋外的部分长度相等,小亮手中有一根长度为cm的细木棒,现从信封内随机取出两根细木棒与小亮手中的细木棒首尾相接放在一起,求抽出的细木棒能与小亮手中的细木棒构成直角三角形的概率(用画树状图或列表的方法求解)23. 习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲、乙两种农机具,已知1件甲种农机具比1件乙种农机具多1.5万元,用18万元购买甲种农机具的数量和用12万元购买乙种农机具的数量相同.(1)、求购买1件甲种农机具和1件乙种农机具各需多少万元?(2)、若该粮食生产基地计划购买甲、乙两种农机具共20件,且购买的总费用不超过72.6万元,则甲种农机具最多能购买多少件?24. “五一”节期间,洞庭湖旅游度假区特色文旅活动精彩上演,吸引众多市民打卡游玩,许多露营爱好者在大烟囱草坪露营,为遮阳和防雨游客们搭建了一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合, , .
(2)、在某次数学活动中,有一个不透明的信封内装有三根长度分别为4cm,6cm和8cm的细木棒,木棒露出纸袋外的部分长度相等,小亮手中有一根长度为cm的细木棒,现从信封内随机取出两根细木棒与小亮手中的细木棒首尾相接放在一起,求抽出的细木棒能与小亮手中的细木棒构成直角三角形的概率(用画树状图或列表的方法求解)23. 习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲、乙两种农机具,已知1件甲种农机具比1件乙种农机具多1.5万元,用18万元购买甲种农机具的数量和用12万元购买乙种农机具的数量相同.(1)、求购买1件甲种农机具和1件乙种农机具各需多少万元?(2)、若该粮食生产基地计划购买甲、乙两种农机具共20件,且购买的总费用不超过72.6万元,则甲种农机具最多能购买多少件?24. “五一”节期间,洞庭湖旅游度假区特色文旅活动精彩上演,吸引众多市民打卡游玩,许多露营爱好者在大烟囱草坪露营,为遮阳和防雨游客们搭建了一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合, , . (1)、天晴时打开“天幕”,若 , 求遮阳宽度(结果精确到0.1m);(2)、下雨时收拢“天幕”, 从减少到 , 求点下降的高度(结果精确到0.1m).
(1)、天晴时打开“天幕”,若 , 求遮阳宽度(结果精确到0.1m);(2)、下雨时收拢“天幕”, 从减少到 , 求点下降的高度(结果精确到0.1m).(参考数据: , , , )
25. 如图,在△ABC中,点D在边AC上,BD平分∠ABC,经过点B、C的⊙O交BD于点E,连接OE交BC于点F,OF⊥BC. (1)、求证:AB是⊙O的切线;(2)、若AB=BC,BD= , tan∠CBD , 求⊙O的半径.
(1)、求证:AB是⊙O的切线;(2)、若AB=BC,BD= , tan∠CBD , 求⊙O的半径.四、填空题
-
26.(1)、【操作发现】
如图1,点M是中边的中点.

请你用圆规和无刻度的直尺过点M作的平行线 , 交于点N;
(2)、在(1)的条件下,线段与的数量关系是;(3)、【类比探究】如图2,线段与射线有公共端点A,请你用圆规和无刻度的直尺在线段上作一个点N,使 .

五、解答题
-
27. 如图,抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点, .
 (1)、求抛物线的函数表达式;(2)、如图1,连接BC,点P在抛物线上,且 , 求点P的坐标;(3)、如图2,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点, , 点M到x轴的距离为2L,的面积为5L,且 , 请问的长是否为定值?如果是,请直接写出这个定值;如果不是,请说明理由.28. 翻开数学发展史,我们就知道数学不仅是抽象、严谨的,还有另外一面,人类从结绳计数开始就在进行着数学实验,并且通过实验不断发展数学,可见,数学实验不仅是数学家研究数学的方式,也是学生学习数学的一种重要方式,在某次数学社团活动中,几位同学利用三角板进行了如下的实数学验,请大家在这一数学实验的基础上思考并回答相关问题:几位同学把两块完全相同的等腰直角三角板按图1方式摆放,已知 , , , , , 线段在直线上,点F在线段上,点A与点D重合.
(1)、求抛物线的函数表达式;(2)、如图1,连接BC,点P在抛物线上,且 , 求点P的坐标;(3)、如图2,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点, , 点M到x轴的距离为2L,的面积为5L,且 , 请问的长是否为定值?如果是,请直接写出这个定值;如果不是,请说明理由.28. 翻开数学发展史,我们就知道数学不仅是抽象、严谨的,还有另外一面,人类从结绳计数开始就在进行着数学实验,并且通过实验不断发展数学,可见,数学实验不仅是数学家研究数学的方式,也是学生学习数学的一种重要方式,在某次数学社团活动中,几位同学利用三角板进行了如下的实数学验,请大家在这一数学实验的基础上思考并回答相关问题:几位同学把两块完全相同的等腰直角三角板按图1方式摆放,已知 , , , , , 线段在直线上,点F在线段上,点A与点D重合. (1)、 , ;(2)、将三角板的直角顶点F沿方向滑动,同时顶点D沿方向在射线上滑动,如图2.
(1)、 , ;(2)、将三角板的直角顶点F沿方向滑动,同时顶点D沿方向在射线上滑动,如图2.①当点F恰好是线段中点时,求的度数;
②当点F从初始位置滑动到点A处时,请直接写出点E所经过的路径长;
(3)、在(2)的条件下,过点D,F分别作 , 的垂线,两条垂线相交于点P,连接 , 线段的长度是否为定值?如果是,请求出结果;如果不是,请说明理由.
-