吉林省长春市朝阳区2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 2023的____是-2023,则横线上可填写的数学概念名词是( )A、倒数 B、平方 C、绝对值 D、相反数2. 如图,一个正方体的三个面上分别标有汉字数、学、美,不考虑汉字方向,则它的展开图可能是下面四个展开图中的( )
 A、
A、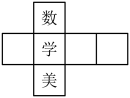 B、
B、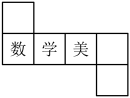 C、
C、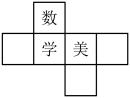 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 方程的根的情况是( )A、没有实数根 B、有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图,的弦、交于点E.若 , , 则的度数是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 方程的根的情况是( )A、没有实数根 B、有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图,的弦、交于点E.若 , , 则的度数是( )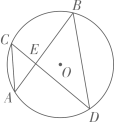 A、 B、 C、 D、6. 如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的 , 若山的高度米,则缆车索道的长为( )
A、 B、 C、 D、6. 如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的 , 若山的高度米,则缆车索道的长为( )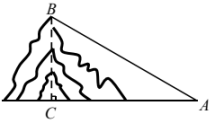 A、米 B、米 C、米 D、米7. 如图,利用内错角相等,两直线平行,我们可以用尺规作图的方法,过的边上一点作的平行线 . 有以下顺序错误的作图步骤:①作射线;②以O为圆心,以任意长为半径画圆弧,分别交、于点C、D;③以F为圆心,长为半径画圆弧,交前面的圆弧于点G;④在边上取一点E,以E为圆心,长为半径画圆弧,交于点F.这些作图步骤的正确顺序为( )
A、米 B、米 C、米 D、米7. 如图,利用内错角相等,两直线平行,我们可以用尺规作图的方法,过的边上一点作的平行线 . 有以下顺序错误的作图步骤:①作射线;②以O为圆心,以任意长为半径画圆弧,分别交、于点C、D;③以F为圆心,长为半径画圆弧,交前面的圆弧于点G;④在边上取一点E,以E为圆心,长为半径画圆弧,交于点F.这些作图步骤的正确顺序为( ) A、①②③④ B、③②④① C、②④③① D、④③①②8. 如图,在平面直角坐标系中,一块墨迹遮挡了横轴的位置,只留下部分纵轴和部分正方形网格,该网格的每个小正方形的边长都是2个单位长度,每个小正方形的顶点叫格点.若格点A、B在函数的图象上,则k的值为( )
A、①②③④ B、③②④① C、②④③① D、④③①②8. 如图,在平面直角坐标系中,一块墨迹遮挡了横轴的位置,只留下部分纵轴和部分正方形网格,该网格的每个小正方形的边长都是2个单位长度,每个小正方形的顶点叫格点.若格点A、B在函数的图象上,则k的值为( )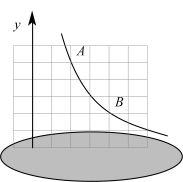 A、6 B、12 C、24 D、48
A、6 B、12 C、24 D、48二、填空题
-
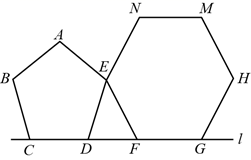
9. 不等式的解集为 .10. 分解因式: .11. 如图,正五边形ABCDE和正六边形EFGHMN的边CD、FG在直线l上,正五边形在正六边形左侧,两个正多边形均在l的同侧,则 的大小是度.
 12. 中国古代数学家赵爽用四个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,为直角三角形中的较大锐角,则tan=.
12. 中国古代数学家赵爽用四个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,为直角三角形中的较大锐角,则tan=. 13. 如图,为直径,点是上的一点,连结、 , 以为圆心,长为半径画圆弧,使点在该圆弧上,再将分别沿、向内翻折.若= , 则图中阴影部分图形的面积和为 . (结果保留)
13. 如图,为直径,点是上的一点,连结、 , 以为圆心,长为半径画圆弧,使点在该圆弧上,再将分别沿、向内翻折.若= , 则图中阴影部分图形的面积和为 . (结果保留) 14. 如图,在平面直角坐标系中,为坐标原点,点在抛物线上,过点作轴的垂线,交抛物线于另一点 , 点、在线段上,且、两点关于轴对称,过点作轴的垂线交抛物线于点 . 连接 , 若 , 则线段的长为 .
14. 如图,在平面直角坐标系中,为坐标原点,点在抛物线上,过点作轴的垂线,交抛物线于另一点 , 点、在线段上,且、两点关于轴对称,过点作轴的垂线交抛物线于点 . 连接 , 若 , 则线段的长为 .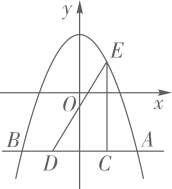
三、解答题
-
15. 先化简,再求值: , 其中 .16. 如图,三张不透明的卡片,正面图案分别是神舟十三号、十四号和十五号纪念图章,依次记为A、B、C,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀.小明从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求小明两次抽到图案上纪念图章相同的概率.
 17. 电子商务的迅速崛起,带来了物流运输和配送的巨大需求.某快递公司采购A、B两种型号的机器人进行5公斤以下的快递分拣,已知A型机器人比B型机器人每小时多分拣10件快递,且A型机器人分拣700件快递所用的时间与B型机器人分拣600件快递所用的时间相同,求B型机器人每小时分拣快递的件数.18. 如图,在中, , 是边的中线,过点D作 , 且 , 连接交于F.
17. 电子商务的迅速崛起,带来了物流运输和配送的巨大需求.某快递公司采购A、B两种型号的机器人进行5公斤以下的快递分拣,已知A型机器人比B型机器人每小时多分拣10件快递,且A型机器人分拣700件快递所用的时间与B型机器人分拣600件快递所用的时间相同,求B型机器人每小时分拣快递的件数.18. 如图,在中, , 是边的中线,过点D作 , 且 , 连接交于F. (1)、求证:四边形是菱形.(2)、若 , 菱形的面积为 , 则的值为 .19. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点.的顶点均在格点,点D为上一格点,点E为上任一点,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)、求证:四边形是菱形.(2)、若 , 菱形的面积为 , 则的值为 .19. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点.的顶点均在格点,点D为上一格点,点E为上任一点,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留作图痕迹.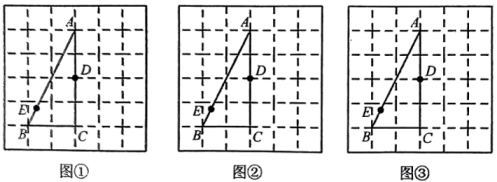 (1)、在图①中画的中位线 , 使点F在边上.(2)、在图②中画以为对角线的 .(3)、在图③中作射线 , 在其上找到一点H,使 .20. 为了解我国2022年25个地区第一季度快递业务收入情况,收集了这25个地区第一季度快递业务收入(单位:亿元)的数据,并对数据进行了整理、描述和分析,给出如下信息.
(1)、在图①中画的中位线 , 使点F在边上.(2)、在图②中画以为对角线的 .(3)、在图③中作射线 , 在其上找到一点H,使 .20. 为了解我国2022年25个地区第一季度快递业务收入情况,收集了这25个地区第一季度快递业务收入(单位:亿元)的数据,并对数据进行了整理、描述和分析,给出如下信息.
a.排在前5位的地区第一季度快递业务收入的数据分别为:
5349 437.0 270.3 187.7 104.0b.其余20个地区第一季度快递业务收入的数据的频数分布表如下:
快递业务收入x
频数
6
10
1
3
c.第一季度快递业务收入的数据在这一组的是:
20.2 20.4 22.4 24.2 26.1 26.5 28.5 34.4 39.1 39.8d.排在前5位的地区、其余20个地区、全部25个地区第一季度快递业务收入的数据的平均数、中位数如下:
前5位的地区
其余20个地区
全部25个地区
平均数
306.8
29.9
n
中位数
270.3
m
28.5
根据以上信息,回答下列问题:
(1)、表中m的值为;(2)、在下面3个数中,与表中n的值最接近的是(填写序号);①30 ②85 ③150
(3)、根据(2)中的数据,预计这25个地区2022年全年快递业务收入约为亿元.21. 某食品加工厂的甲、乙两个生产组领到了相同的加工任务,甲、乙两组以相同的工作效率同时开始工作,中途乙组因升级设备,停工了一段时间.乙组设备升级完毕后,提高了工作效率,在完成本组任务后,并帮助甲组加工了60 kg食品,最后两组同时停工,完成了此次加工任务,两组各自加工的食品量y(kg)与甲组工作时间x(h)之间的函数图象如图所示.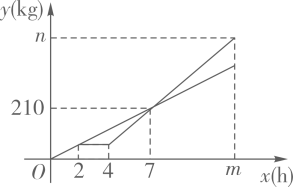 (1)、甲组每小时加工食品kg,乙组升级设备后每小时加工食品kg.(2)、求乙组设备升级完毕后y与x之间的函数关系式.(3)、求m、n的值.22. 【题目】如图①,在矩形ABCD中, , F是AB延长线上一点,且 , 连结DF,交BC于点E,连结AE.试判断线段AE与DF的位置关系.
(1)、甲组每小时加工食品kg,乙组升级设备后每小时加工食品kg.(2)、求乙组设备升级完毕后y与x之间的函数关系式.(3)、求m、n的值.22. 【题目】如图①,在矩形ABCD中, , F是AB延长线上一点,且 , 连结DF,交BC于点E,连结AE.试判断线段AE与DF的位置关系.
【探究展示】小明发现, , 并展示了如下的证明方法:
证明:∵ ,
∴ .
∵ ,
∴ .
∵四边形ABCD是矩形,
∴ .
∴ .
∵ ,
∴ .
∴ .
∵ ,
∴ . (依据)
(1)、【反思交流】上述证明过程中的“依据”是 .(2)、小颖受到小明的启发,继续进行探究,如图②,连结图①中的 , 将绕着点顺时针旋转得到 , 连结 . 求证:点在线段的垂直平分线上.(3)、【拓展应用】如图③,将图①中的绕着点顺时针旋转得到 . 分别以点、为圆心,以长为半径作弧,两弧交于点 , 连结 . 若 , 直接写出的值.23. 如图,在中, , , , 是对角线,E为边的中点.点P从点A出发,沿AD以每秒1个单位长度的速度向终点D运动,在线段的延长线上取一点Q,使 , 以为斜边向其右侧作 , 使 . 连接 , 作点A关于的对称点 , 连接 , 设点P运动的时间为t秒(). (1)、的长为 .(2)、用含t的代数式表示线段的长.(3)、当点在边上时,求与重叠部分图形的面积;(4)、当时,直接写出t的值.24. 在平面直角坐标系中,点为坐标原点,抛物线的对称轴为直线 , 点、在该抛物线上(点与点不重合),其横坐标分别为、 . 该抛物线在、两点之间的部分(包括、两点)记为图象 .(1)、求该抛物线对应的函数关系式.(2)、当图象的对应的函数值随的增大而减小时,求的取值范围.(3)、当抛物线的顶点是图象的最低点时,设图象的最高点与最低点的纵坐标之差为 , 求与之间的函数关系式,并写出自变量的取值范围.(4)、过、两点中较低的点作轴的垂线交图象于另一个交点 , 以这个较低的点与点的连线为边向其下方作正方形,当点在该正方形内部,且抛物线的顶点到该正方形的边的最小距离是时,直接写出的值.
(1)、的长为 .(2)、用含t的代数式表示线段的长.(3)、当点在边上时,求与重叠部分图形的面积;(4)、当时,直接写出t的值.24. 在平面直角坐标系中,点为坐标原点,抛物线的对称轴为直线 , 点、在该抛物线上(点与点不重合),其横坐标分别为、 . 该抛物线在、两点之间的部分(包括、两点)记为图象 .(1)、求该抛物线对应的函数关系式.(2)、当图象的对应的函数值随的增大而减小时,求的取值范围.(3)、当抛物线的顶点是图象的最低点时,设图象的最高点与最低点的纵坐标之差为 , 求与之间的函数关系式,并写出自变量的取值范围.(4)、过、两点中较低的点作轴的垂线交图象于另一个交点 , 以这个较低的点与点的连线为边向其下方作正方形,当点在该正方形内部,且抛物线的顶点到该正方形的边的最小距离是时,直接写出的值.