吉林省松原市宁江区2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下列实数:3.1416, , , , -1,其中无理数的个数有( )A、1个 B、2个 C、3个 D、4个2. 在我国《“十四五”就业促进规划》中明确提出,到2025年,城镇新增就业5500万人以上,数据5500万用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的石板凳,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 不等式的解集在数轴上表示正确的是( )A、
4. 不等式的解集在数轴上表示正确的是( )A、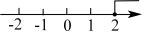 B、
B、 C、
C、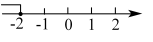 D、
D、 5. 如图,四边形内接于 , 则的半径为( )
5. 如图,四边形内接于 , 则的半径为( ) A、4 B、 C、 D、6. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )
A、4 B、 C、 D、6. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、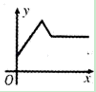
二、填空题
-
7. 因式分解:= .8. 关于的一元二次方程有两个实数根,则的取值范围是.9. 《九章算术》是中国古代重要的数学专著,有一问题的译文为:上等谷2束,下等谷1束,可得粮食13斗;上等谷1束,下等谷1束,可得粮食8斗,求每束上等谷和下等谷各多少斗?设每束上等谷x斗,每束下等谷y斗,则可列方程组为 .10. 如图,在中,D是上一点, , , 垂足为E,F是的中点, , 则的长为 .
 11. 如图,在中, , , 是的平分线,经过 , 两点的圆的圆心恰好落在上,分别与、相交于点、若圆半径为则阴影部分面积 .
11. 如图,在中, , , 是的平分线,经过 , 两点的圆的圆心恰好落在上,分别与、相交于点、若圆半径为则阴影部分面积 . 12. 抛物线的顶点D在直线上运动,顶点运动时抛物线也随之运动,抛物线与直线相交于点Q,则点Q纵坐标的最大值为.13. 某校数学兴趣小组为测量学校旗杆的高度,利用测角仪及皮尺测得以下数据:如图, , , , 已知测角仪的高度为 , 则旗杆的高度约为m.(结果精确到 , 参考数据:)
12. 抛物线的顶点D在直线上运动,顶点运动时抛物线也随之运动,抛物线与直线相交于点Q,则点Q纵坐标的最大值为.13. 某校数学兴趣小组为测量学校旗杆的高度,利用测角仪及皮尺测得以下数据:如图, , , , 已知测角仪的高度为 , 则旗杆的高度约为m.(结果精确到 , 参考数据:) 14. 如图,在直角坐标系中点 , , 将向右平移,某一时刻,反比例函数的图象恰好经过点A和OB的中点,则k的值为 .
14. 如图,在直角坐标系中点 , , 将向右平移,某一时刻,反比例函数的图象恰好经过点A和OB的中点,则k的值为 .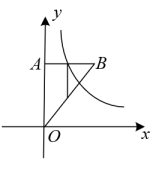
三、解答题
-
15. 计算: .16. 先化简,再求值:其中 , .17. 某校开展“强国学习”知识竞赛,现从一队,二队,三队,四队四个队中,随机抽取两个队进行第一轮的抢答PK环节比赛,请用列表或画树状图的方法求出抽到二队和三队比赛的概率.18. 某店有、两种口罩出售,其中种口罩的单价要比种口罩的单价多0.3元,用27元购进种口罩数量是用18元购进种口罩数量的2倍.(1)、求、两种口罩的单价;(2)、某单位从该店购进、两种口罩共1000个,总费用为1080元,求购进种口罩多少个.19. 如图,图①、图②均是的正方形网格,每个小正方形的边长均为 , 每个小正方形的顶点称为格点,点、、均为格点只用无刻度的直尺,按下列要求作图:
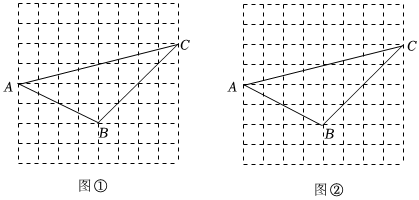 (1)、在图①中,作的边上的高;(2)、在图②中,过点作直线 , 使得直线平分的面积.20. 如图,在平行四边形中,边的垂直平分线交于点E,交的延长线于点F,连接 , .
(1)、在图①中,作的边上的高;(2)、在图②中,过点作直线 , 使得直线平分的面积.20. 如图,在平行四边形中,边的垂直平分线交于点E,交的延长线于点F,连接 , .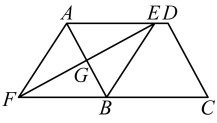 (1)、求证:;(2)、求证:四边形是菱形.21. 为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)、求证:;(2)、求证:四边形是菱形.21. 为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.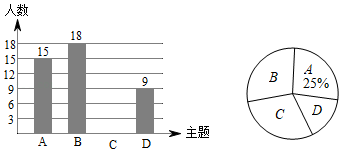 (1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“B”所在扇形的圆心角等于度;(4)、小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.22. 华山古称“西岳”,为五岳之一,中华的“华”源于华山,因此华山有了“华夏之根”之称,华山南接秦岭山脉,北瞰黄渭,自古以来就有“奇险天下第一山”的说法.甲、乙两人住同一小区,该小区到华山的距离为300千米,两人先后从家出发沿同一路线驾车驶向华山,如图,线段表示甲离开家的距离y(千米)与时间t(小时)之间的函数关系;线段表示乙离开家的距离y(千米)与时间t(小时)之间的函数关系.点C在线段上,请根据图象解答下列问题:
(1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“B”所在扇形的圆心角等于度;(4)、小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.22. 华山古称“西岳”,为五岳之一,中华的“华”源于华山,因此华山有了“华夏之根”之称,华山南接秦岭山脉,北瞰黄渭,自古以来就有“奇险天下第一山”的说法.甲、乙两人住同一小区,该小区到华山的距离为300千米,两人先后从家出发沿同一路线驾车驶向华山,如图,线段表示甲离开家的距离y(千米)与时间t(小时)之间的函数关系;线段表示乙离开家的距离y(千米)与时间t(小时)之间的函数关系.点C在线段上,请根据图象解答下列问题: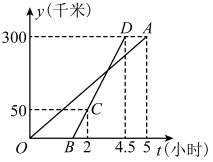 (1)、求点B的坐标;(2)、在整个过程中 , 求t为何值时,甲、乙两人之间的距离恰好为30千米.23. 如图,为⊙的直径,点是⊙上一点,过点的直线交的延长线于点 . 作 , 垂足为点 , 已知平分 .
(1)、求点B的坐标;(2)、在整个过程中 , 求t为何值时,甲、乙两人之间的距离恰好为30千米.23. 如图,为⊙的直径,点是⊙上一点,过点的直线交的延长线于点 . 作 , 垂足为点 , 已知平分 .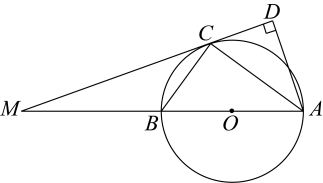 (1)、求证:是⊙的切线;(2)、若 , , 求⊙的半径.24. 如图,在平行四边形中, , 垂足为 , 平分 , 交线段于点 .
(1)、求证:是⊙的切线;(2)、若 , , 求⊙的半径.24. 如图,在平行四边形中, , 垂足为 , 平分 , 交线段于点 .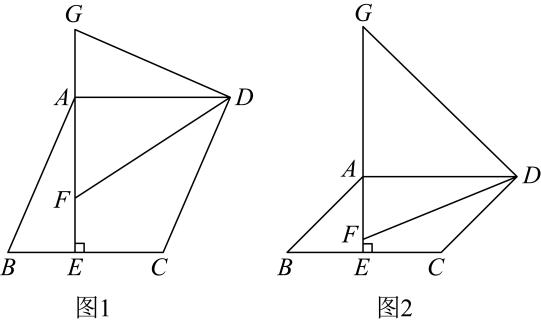 (1)、如图1,延长到点 , 使得 , 连接 .
(1)、如图1,延长到点 , 使得 , 连接 .①若 , 则 ▲ °(用含有α的代数式表示);
②若 , 求证: .
(2)、如图2,延长到点 , 使得 , 连接 . 若 , 用等式表示线段 , , 之间的数量关系,直接写出结果(不需证明).25. 如图,在中, , , , 点为边上的点,且 . 动点从点出发(点不与点、重合),沿以每秒1个单位长度的速度向终点运动,同时点从点出发,以相同的速度沿折线向终点运动,以、为邻边构造 , 设点运动的时间为()秒.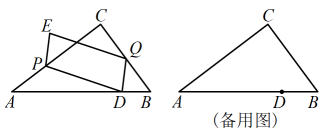 (1)、当点与点重合时,的值为;(2)、当点落在边上时,求的值;(3)、设的面积为(),求与之间的函数关系式;(4)、连接 , 直接写出与的边平行时的值.26. 如图,抛物线与x轴交于点 与y轴交于点C,点A的坐标为 .
(1)、当点与点重合时,的值为;(2)、当点落在边上时,求的值;(3)、设的面积为(),求与之间的函数关系式;(4)、连接 , 直接写出与的边平行时的值.26. 如图,抛物线与x轴交于点 与y轴交于点C,点A的坐标为 . (1)、求b的值和点B,C的坐标;(2)、若点D为的中点,点P为第一象限内抛物线上的一点,过点P作轴,垂足为H,与分别交于点 , 且 , 求点P的坐标;(3)、若直线与抛物线交于两点,且有一个交点在第一象限,其中 , 若结合函数图象,探究n的取值范围.
(1)、求b的值和点B,C的坐标;(2)、若点D为的中点,点P为第一象限内抛物线上的一点,过点P作轴,垂足为H,与分别交于点 , 且 , 求点P的坐标;(3)、若直线与抛物线交于两点,且有一个交点在第一象限,其中 , 若结合函数图象,探究n的取值范围.