湖南省张家界市永定区2023年中考一模数学试题

试卷更新日期：2023-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 2023的相反数是（）

A、-2023 B、 $| 2023 |$ C、 $- \frac{1}{2023}$ D、 $\frac{1}{2023}$

查看试题解析
2. 下列选项中的图案既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列性质中，矩形不一定具有的是（）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、邻边互相垂直

查看试题解析
4. 下列各组数中，两数不相等的是（）

A、 ${(- 3)}^{2}$ 与 $- 3^{2}$ B、 ${(- 3)}^{2}$ 与 $3^{2}$ C、 ${(- 2)}^{3}$ 与 $- 2^{3}$ D、 ${| - 2 |}^{3}$ 与 $| - 2^{3} |$

查看试题解析
5. 如图， $C D ⊥ A B$ 于点 $D$ ， $E F ⊥ A B$ 于点 $F$ ， $C D = E F$ ．要根据 $H L$ 证明 $R t △ A C D ≌ R t △ B E F$ ，则还需要添加的条件是（）

A、 $∠ A = ∠ B$ B、 $∠ C = ∠ E$ C、 $A D = B F$ D、 $A C = B E$

查看试题解析
6. 11的算术平方根是（）

A、121 B、 $- \sqrt{11}$ C、 $\sqrt{11}$ D、 $\pm \sqrt{11}$

查看试题解析
7. 下列成语所描述的事件属于不可能事件的是（）

A、守株待兔 B、水中捞月 C、水滴石穿 D、百发百中

查看试题解析
8. 如图，在直角坐标系中，以坐标原点 $O (0 ， 0)$ ， $A (0 ， 4)$ ， $B (3 ， 0)$ 为顶点的 $R t △ A O B$ ，其两个锐角对应的外角角平分线相交于点 $P$ ，且点 $P$ 恰好在反比例函数 $y = \frac{k}{x}$ 的图象上，则 $k$ 的值为（）

A、36 B、25 C、16 D、9

查看试题解析

二、填空题

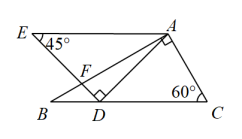
9. 太阳的半径约为 $696000000 m$ ，用科学记数法表示696000000为．

查看试题解析
10. 已知一组数据：6、a、3、4、8、7的众数为6，则这组数据的中位数是．

查看试题解析
11. 将一副三角板如图所示放置，使点D在 $B C$ 上， $B C ∥ A E$ ，则 $∠ E F B$ 的度数为．

查看试题解析
12. 已知关于 $x$ 的方程 $x^{2} + 2 x - a = 0$ 的一个根为 $2$ ，则另一个根是．

查看试题解析
13. 不等式组 ${\begin{array}{l} 3 x - 9 > 0 \\ x > m \end{array}$ 的解集为 $x > 3$ ，则m的取值范围为．

查看试题解析
14. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有5个结论：① $a b c > 0$ ；② $b > a + c$ ；③ $9 a + 3 b + c > 0$ ； ④ $c < - 3 a$ ； ⑤ $a + b \geq m (a m + b)$ ，其中正确的有是．

查看试题解析

三、解答题

15. 计算： $- 1^{2022} + | \sqrt{3} - 2 | + t a n 60 ° + (π - 3.14)^{0} + (\frac{1}{2})^{- 2}$ ．

查看试题解析
16. 先化简，再求值： $\frac{x - 3}{x^{2} - 1} \div \frac{x - 3}{x^{2} + 2 x + 1} - (\frac{1}{x - 1} + 1)$ ，其中x从 $- 1$ ， 0，1，2，3中选取一个合适的数．

查看试题解析
17. 某新能源汽车经销商购进A、B两种型号的新能源汽车，据了解2辆A型汽车、3辆B型汽车的进价共计88万元；3辆A型汽车、2辆B型汽车的进价共计92万元．

(1)、求A、B两种型号汽车的进货单价；

(2)、由于新能源汽车需求不断增加，该店准备购进A，B两种型号的新能源汽车60辆，已知A型车的售价为25万元/辆，B型车的售价为20万元/辆．根据销售经验，购进B型车的数量不少于A型车的2倍，设购进a辆A型车，60辆车全部售完获利w万元，该经销商应购进A，B两种型号车各多少辆，才能使w最大？w最大为多少万元？

查看试题解析
18. 如图，已知四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点O，O是 $B D$ 的中点，E，F是 $B D$ 上的点，且 $B E ＝ D F$ ， $A F ∥ C E$ ．

(1)、求证： $△ O E C ≌ △ O F A$ ；

(2)、若 $O A ＝ O B$ ，求证：四边形ABCD是矩形．

查看试题解析
19. 每年的4月15日是我国全民国家安全教育日．某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）．相关数据统计、整理如下：
八年级抽取的学生的竞赛成绩：

4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10．

七、八年级抽取的学生的竞赛成绩统计表

年级七年级八年级

平均数 7.4 7.4

中位数 a b

众数 7 c

合格率 85% 90%

根据以上信息，解答下列问题：

(1)、填空：a= ， b= ， c= ．

(2)、估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；

(3)、根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异．

查看试题解析
20. 空中缆车是旅游时上、下山和进行空中参观的交通工具．小明一家去某著名风景区旅游，准备先从山脚A走台阶步行到B，再换乘缆车到山顶C．从A到B的路线可看作是坡角为30°的斜坡，长度为1200米；从B到C的缆车路线可看作是直线，其与水平线的夹角为45°，且缆车从B到C的平均速度为6米/秒，运行时间为10分钟，求山顶C到AD的距离（结果保留根号）．

查看试题解析
21. 在日历上，我们可以发现其中某些数满足一定的规律，如图是2019年1月份的日历．我们任意选择其中所示的菱形框部分，将每个菱形框部分中去掉中间位置的数之后，相对的两对数分别相乘，再相减，例如： $9 \times 11 - 3 \times 17 = 48$ ， $13 \times 15 - 7 \times 21 = 48$ ．不难发现，结果都是48．

(1)、请证明发现的规律；

(2)、若用一个如图所示菱形框，再框出5个数字，其中最小数与最大数的积为435，求出这5个数中的最大数；

(3)、嘉琪说：她用一个如图所示菱形框，框出5个数字，其中最小数与最大数的积是95，直接判断他的说法是否正确（不必叙述理由）．

查看试题解析
22. 如图，点 $D$ 在 $⊙ O$ 的直径 $A B$ 的延长线上，点 $C$ 在 $⊙ O$ 上， $A C$ 平分 $∠ D A E$ ， $A E ⊥ C D$ 于点 $E$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线．

(2)、 $D F$ 是 $⊙ O$ 的切线， $F$ 为切点，若 $B D = 2$ ， $∠ A D E = 30 °$ ，求 $\overset{⌢}{A F}$ 的长．

查看试题解析
23. 已知抛物线与 $x$ 轴交于点 $A (- 1 ， 0)$ 、 $B (3 ， 0)$ ，与 $y$ 轴交于点 $C (0 ， 3)$ .

(1)、求抛物线解析式；

(2)、如图①，若点 $P$ 是第一象限内抛物线上一动点，过点 $P$ 作 $P D ⊥ B C$ 于点 $D$ ，求线段 $P D$ 长的最大值

(3)、如图②，若点 $N$ 是抛物线上另一动点，点 $M$ 是平面内一点，是否存在以点 $B$ 、 $C$ 、 $M$ 、 $N$ 为顶点，且以 $B C$ 为边的矩形，若存在，求出点 $M$ 的坐标；若不存在，请说明理由

查看试题解析

年级	七年级	八年级
平均数	7.4	7.4
中位数	a	b
众数	7	c
合格率	85%	90%