黑龙江省绥化市2023年中考一模数学试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. ±2是4的( )A、平方根 B、相反数 C、绝对值 D、倒数2. 下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1 , S2 , S3 , 则S1 , S2 , S3的大小关系是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1 , S2 , S3 , 则S1 , S2 , S3的大小关系是( )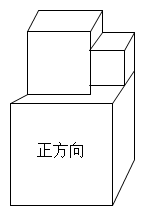 A、S1>S2>S3 B、S3>S2>S1 C、S2>S3>S1 D、S1>S3>S25. 在函数中,自变量x的取值范围是( )A、 B、 C、且 D、6. 下列命题是真命题的是( )A、“对顶角相等”的逆命题是真命题 B、平行线的同旁内角的平分线互相垂直 C、和为的两个角叫做邻补角 D、在同一平面内, , , 是直线,且 , , 则7. 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至的位置,点B的横坐标为2,则点的坐标为( )
A、S1>S2>S3 B、S3>S2>S1 C、S2>S3>S1 D、S1>S3>S25. 在函数中,自变量x的取值范围是( )A、 B、 C、且 D、6. 下列命题是真命题的是( )A、“对顶角相等”的逆命题是真命题 B、平行线的同旁内角的平分线互相垂直 C、和为的两个角叫做邻补角 D、在同一平面内, , , 是直线,且 , , 则7. 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至的位置,点B的横坐标为2,则点的坐标为( ) A、(1,1) B、() C、(-1,1) D、()8. 某企业1~5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( ).
A、(1,1) B、() C、(-1,1) D、()8. 某企业1~5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( ).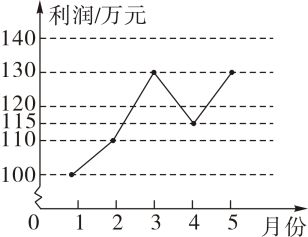 A、1~2月份利润的增长快于2~3月份利润的增长 B、1~4月份利润的极差与1~5月份利润的极差不同 C、1~5月份利润的众数是130万元 D、1~5月份利润的中位数为120万元9. 有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )A、 B、 C、 D、10. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、
A、1~2月份利润的增长快于2~3月份利润的增长 B、1~4月份利润的极差与1~5月份利润的极差不同 C、1~5月份利润的众数是130万元 D、1~5月份利润的中位数为120万元9. 有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )A、 B、 C、 D、10. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、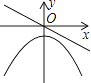 B、
B、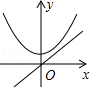 C、
C、 D、
D、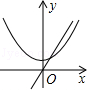 11. 如图,火车匀速通过隧道(隧道长等于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( )
11. 如图,火车匀速通过隧道(隧道长等于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( )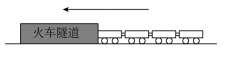 A、
A、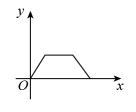 B、
B、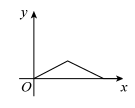 C、
C、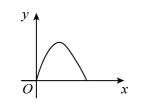 D、
D、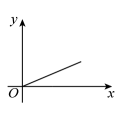 12. 如图,正方形中, , , 分别交 , 于点M,N.下列结论:①;②;③;④ . 其中结论正确的个数有( )
12. 如图,正方形中, , , 分别交 , 于点M,N.下列结论:①;②;③;④ . 其中结论正确的个数有( )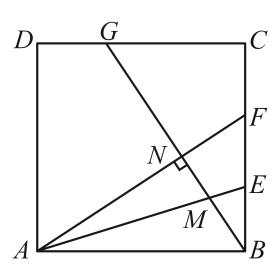 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 某超市有A,B,C三种型号的甲种品牌饮水机和D,E两种型号的乙种品牌饮水机,某中学准备从甲、乙两种品牌的饮水机中各选购一种型号的饮水机安装到教室.如果各种选购方案被选中的可能性相同,那么A型号饮水机被选中的概率是 .14. 分解因式: .15. 若不等式组 有解,则a的取值范围是 .16. 用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .17. 已知x1 , x2是一元二次方程x2+2(m+1)x+m2-1=0的两实数根,且满足(x1-x2)2=16-x1x2 , 实数m的值为 .18. 在平面直角坐标系中,以任意两点 , 为端点的线段的中点坐标为 . 在直角坐标系中,有 , , 三点,另有一点与 , , 构成平行四边形的顶点,则点的坐标为 .19. 如图,正六边形的边长为2,正六边形的外接圆与正六边形的各边相切,正六边形的外接圆与正六边形的各边相切……按这样的规律进行下去,的边长为 .
 20. 宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团20人准备同时租用这三种客房共7间,如果每个房间都住满,租房方案有 种.21. 如图, , , , 分别为菱形各边的中点,连接 , , , 得四边形 , 以此类推得四边形……若菱形的面积为 , 则四边形的面积为 .
20. 宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团20人准备同时租用这三种客房共7间,如果每个房间都住满,租房方案有 种.21. 如图, , , , 分别为菱形各边的中点,连接 , , , 得四边形 , 以此类推得四边形……若菱形的面积为 , 则四边形的面积为 .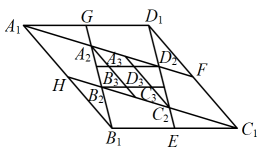 22. 如图,折叠矩形纸片 , 使点对应的点落在边上,折痕的两端分别在 , 上(含端点),且 , , 则折痕长的最大值是 .
22. 如图,折叠矩形纸片 , 使点对应的点落在边上,折痕的两端分别在 , 上(含端点),且 , , 则折痕长的最大值是 .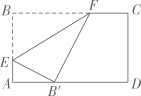
三、解答题
-
23. 如图,中, .
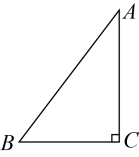 (1)、用直尺和圆规在线段上找一点 , 使点D到和的距离相等;(2)、在(1)的条件下,若 , , 求点D到的距离.24. 某过街天桥的设计图是梯形(如图所示),桥面与地面平行,米,米.左斜面与地面的夹角为 , 右斜面与地面的夹角为 , 立柱于点E,立柱于点F,求桥面与地面之间的距离.(精确到0.1米,参考数据: , . )
(1)、用直尺和圆规在线段上找一点 , 使点D到和的距离相等;(2)、在(1)的条件下,若 , , 求点D到的距离.24. 某过街天桥的设计图是梯形(如图所示),桥面与地面平行,米,米.左斜面与地面的夹角为 , 右斜面与地面的夹角为 , 立柱于点E,立柱于点F,求桥面与地面之间的距离.(精确到0.1米,参考数据: , . ) 25. 如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.
25. 如图,直线L:y=-x+3与两坐标轴分别相交于点A、B. (1)、当反比例函数y=(m>0,x>0)的图象在第一象限内与直线L至少有一个交点时,求m的取值范围.(2)、若反比例函数y=(m>0,x>0)在第一象限内与直线L相交于点C、D,当CD=时,求m的值.(3)、在(2)的条件下,请你直接写出关于x的不等式-x+3<的解集.26. 已知正方形 , P为射线上的一点,以为边作正方形 , 使点F在线段的延长线上,连接 , .
(1)、当反比例函数y=(m>0,x>0)的图象在第一象限内与直线L至少有一个交点时,求m的取值范围.(2)、若反比例函数y=(m>0,x>0)在第一象限内与直线L相交于点C、D,当CD=时,求m的值.(3)、在(2)的条件下,请你直接写出关于x的不等式-x+3<的解集.26. 已知正方形 , P为射线上的一点,以为边作正方形 , 使点F在线段的延长线上,连接 , .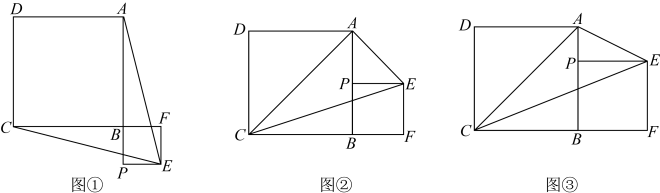 (1)、如图①,若点P在线段的延长线上,求证;(2)、如图②,若P是线段的中点,连接 , 判断的形状,并说明理由;(3)、如图③,若点P在线段上,连接 , 当平分时,设 , , 求的值及的度数.27. 如图所示,半径为1,点是上一点,弦垂直平分线段 , 点是弧上的任一点(与端点、不重合),于点 , 以点为圆心,的长为半径作 , 分别过点、作的切线,两条切线相交于点 .
(1)、如图①,若点P在线段的延长线上,求证;(2)、如图②,若P是线段的中点,连接 , 判断的形状,并说明理由;(3)、如图③,若点P在线段上,连接 , 当平分时,设 , , 求的值及的度数.27. 如图所示,半径为1,点是上一点,弦垂直平分线段 , 点是弧上的任一点(与端点、不重合),于点 , 以点为圆心,的长为半径作 , 分别过点、作的切线,两条切线相交于点 .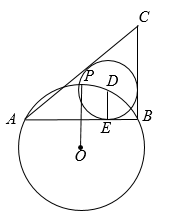 (1)、求弦的长;(2)、判断是否为定值,若是,求的大小;否则,说明理由.(3)、记的面积为 , 若 , 求的周长.28. 已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)、求弦的长;(2)、判断是否为定值,若是,求的大小;否则,说明理由.(3)、记的面积为 , 若 , 求的周长.28. 已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.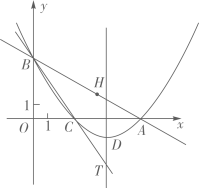 (1)、直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;(2)、若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;(3)、设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA-QO|的取值范围.
(1)、直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;(2)、若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;(3)、设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA-QO|的取值范围.