黑龙江省哈尔滨市香坊区2023年中考一模数学试题

试卷更新日期：2023-04-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 哈市某天的最高气温为11℃，最低气温为-6℃，则最高气温与最低气温的差为（）

A、5℃ B、17℃ C、-17℃ D、-5℃

查看试题解析
2. 下列运算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 ${(2 a^{2})}^{3} = 6 a^{6}$ D、 $a^{8} \div a^{2} = a^{4}$

查看试题解析
3. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图的几何体是由一些小正方形组合而成的，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 若方程 ax²+bx+c=0 的两个根是﹣3 和 1，那么二次函数 y=ax²+bx+c 的图象的对称轴是直线（）

A、x=﹣3 B、x=﹣2 C、x=﹣1 D、x=1

查看试题解析
6. 方程 $\frac{2}{3 x - 1}$ = $\frac{3}{x}$ 的解为（）．

A、x= $\frac{3}{11}$ B、x= $\frac{11}{3}$ C、x= $\frac{3}{7}$ D、x= $\frac{7}{3}$

查看试题解析
7. 如图，⊙O中，弦AB，CD相交于点P，∠A=42°，∠APD=77°，则∠B的大小是（）

A、34° B、35° C、43° D、44°

查看试题解析
8. 某种水稻2020年平均每公顷产 $7200 k g$ ， 2022年平均每公顷产 $8450 k g$ ，设该水稻每公顷产量的年平均增长率为x，则下面所列的方程中正确的是（）．

A、 $7200 {(1 - x)}^{2} = 8450$ B、 $7200 {(1 + x)}^{2} = 8450$ C、 $7200 {(1 + 2 x)}^{2} = 8450$ D、 $8450 {(1 - x)}^{2} = 7200$

查看试题解析
9. 如图， $M N$ 是 $△ A B C$ 的中位线，点F在线段 $B C$ 上， $C F = 2 B F$ ，连接 $A F$ 交 $M N$ 于点E，下列说法错误的是（）

A、 $\frac{A E}{A F} = \frac{1}{2}$ B、 $\frac{M E}{M N} = \frac{1}{3}$ C、 $\frac{A M}{B M} = \frac{A E}{A F}$ D、 $\frac{M E}{B F} = \frac{A N}{A C}$

查看试题解析
10. 如图，老师开车从甲地去往20千米外的乙地，开始时以一定的速度行驶，之后由于道路维修，速度变为开始时速度的二分之一，过了维修道路后又变为开始时的速度行驶到达乙地，设老师行驶的时间为x（分钟），行驶的路程为y（千米），图中的折线表示y与x之间的函数关系，则老师从甲地到达乙地所用的时间是（）．

A、15分钟 B、20分钟 C、25分钟 D、26分钟

查看试题解析

二、填空题

11. 将数9420000用科学记数法表示为．

查看试题解析
12. 计算 $\sqrt{45} - \frac{\sqrt{20}}{2}$ 的结果是．

查看试题解析
13. 函数 $y = \frac{x + 1}{x - 3}$ 的自变量x的取值范围是．

查看试题解析
14. 把多项式 $a^{3} b - 6 a^{2} b + 9 a b$ 因式分解的结果为.

查看试题解析
15. 不等式组 ${\begin{array}{l} 3 x \geq x - 2 \\ \frac{x + 1}{3} > 2 x \end{array}$ 的解集是．

查看试题解析
16. 如图，在平面直角坐标系中，点O是坐标原点，点A是x轴正半轴上的一个定点，点P是双曲线 $y = \frac{3}{x} (x > 0)$ 上的一个动点， $P B ⊥ y$ 轴于点B，当点P的横坐标逐渐增大时，四边形 $O A P B$ 的面积将会．（填“逐渐增大”或“不变”或“逐渐减小”）

查看试题解析
17. 某扇形的圆心角是45°，面积为 $18 π$ ，该扇形的半径是．

查看试题解析
18. 一个不透明的袋子中装有黑、白小球各两个，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球都是白球的概率为．

查看试题解析
19. $△ A B C$ 中， $∠ B A C = 90 °$ ，点D在直线 $A B$ 上，连接 $C D$ ，若 $t a n ∠ A C D = \frac{1}{2}$ ， $A B = 3$ ， $A D = 2$ ，则 $△ B C D$ 的面积为．

查看试题解析
20. 如图，平行四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O， $A C ⊥ B C$ ，点E是线段 $O D$ 上一点，连接 $A E$ 、 $C E$ ，若 $B C = C E$ ， $A E ⊥ C E$ ， $D E = 2$ ，则线段 $A B$ 长为．

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{x}{x^{2} - 1} \div (1 - \frac{1}{x + 1})$ ，其中 $x = \sqrt{2} sin 45^{\circ} + tan 60^{\circ}$ .

查看试题解析
22. 如图，在每个小正方形的边长均为1的方格纸中有线段AB和CD，点A、B、C、D均在小正方形的顶点上．

(1)、画出一个以AB为一边的△ABE，点E在小正方形的顶点上，且∠BAE＝45°，△ABE的面积为 $\frac{5}{2}$ ；

(2)、画出以CD为一腰的等腰△CDF，点F在小正方形的顶点上，且△CDF的面积为 $\frac{15}{2}$ ；

(3)、在（1）、（2）的条件下，连接EF，请直接写出线段EF的长．

查看试题解析
23. 某小区为了解业主对小区物业服务的满意度，从小区中随机抽取部分住户进行调查，调查结果分为：A．非常满意；B．满意；C．基本满意；D．不满意四个等级．请根据如图所示的两幅统计图中的信息回答下列问题：

(1)、抽样调查共抽取了多少户？

(2)、求本次调查中“基本满意”的有多少户？并补全条形统计图；

(3)、若该小区共有5000户，请估计对该小区服务表示不满意的有多少户？

查看试题解析
24. 已知：四边形ABCD中，AC为对角线，∠DAC＝∠BCA，且AD＝BC，CD⊥AD于点D．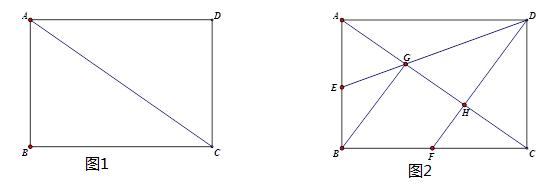

(1)、如图1，求证：四边形ABCD是矩形．

(2)、如图2，点E和点F分别为边AB和边BC的中点，连接DE、DF分别交AC于点G和点H，连接BG，在不连接其它线段的情况下，请写出所有面积是△FHC面积的2倍的所有三角形．

查看试题解析
25. 文教店用1200元购进了甲、乙两种纪念册，已知甲种纪念册进价为每本12元，乙种纪念册进价为每本10元，文教店在销售时甲种纪念册售价为每本15元，乙种纪念册售价为每本12元，全部售完后共获利270元

(1)、求文教店购进甲、乙两种纪念册各多少本？

(2)、若文教店以原进价再次购进甲、乙两种纪念册，且购进甲种纪念册的数量不变，而购进乙种纪念册的数量是第一次的2倍，乙种纪念册按原售价销售，而甲种纪念册降价销售，当两种纪念册销售完毕时，要使再次购进的纪念册获利不少于340元，求甲种纪念册每本最低售价应为多少元？

查看试题解析
26. 已知， $A B$ 为 $⊙ O$ 的直径，弦 $C D$ 与 $A B$ 交于点E，点A为弧 $C D$ 的中点．

(1)、如图1，求证： $A B ⊥ C D$ ；

(2)、如图2，点F为弧 $B C$ 上一点，连接 $B F$ ， $B D$ ， $∠ F B A = 2 ∠ D B A$ ，过点C作 $C G ∥ A B$ 交 $B F$ 于点G，求证： $C G = \frac{1}{2} A B$ ．

(3)、如图3，在（2）的条件下，连接 $D F$ 交 $O E$ 于点L，连接 $L G$ ，若 $F G = 4$ ， $t a n ∠ G L B = \frac{\sqrt{7}}{3}$ ，求线段 $L F$ 的长．

查看试题解析
27. 在平面直角坐标系中，点O为坐标原点，抛物线 $y = a x^{2} + b$ 与x轴负半轴相交于点A，与x轴正半轴相交于点B，与y轴正半轴相交于点C， $A O = O C = 6$ ．

(1)、求a，b的值；

(2)、如图1，点P为第一象限抛物线上一点，设点P的横坐标为t，连接 $P O$ 、 $P B$ ，设 $△ P O B$ 的面积为S，求S与t的函数关系式．（不要求写出自变量t的取值范围）；

(3)、如图2，在（2）的条件下，连接 $C P$ ，过点P作 $P D ⊥ C P$ 交y轴于点D，过点D作y轴的垂线交第三象限内的抛物线于点Q，连接 $P Q$ ，点F在y轴上，且在点C上方，点G为y轴负半轴上一点，且 $C F = O G$ ，连接 $A F$ 、 $B G$ ，点H在 $A F$ 上，过点F作 $F M ⊥ y$ 轴交 $O H$ 延长线于点M， $O H = M H$ ，点N为 $O C$ 上一点，连接 $N H$ ， $∠ B G O + ∠ H N O$ $= 180 °$ ，连接 $A N$ ，若 $A N ∥ P Q$ ，求点Q的坐标．

查看试题解析