广东省深圳市南山区2023年中考二模数学试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 如图所示的空心圆柱,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 2022年世界杯在卡塔尔举办,为了办好这届世界杯,人口仅有280万的卡塔尔投资2200亿美元修建各项设施,数据2200亿用科学记数法表示为( )A、 B、 C、 D、3. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、4. 如图,函数和的图象相交于点 , 则不等式的解集为( )
2. 2022年世界杯在卡塔尔举办,为了办好这届世界杯,人口仅有280万的卡塔尔投资2200亿美元修建各项设施,数据2200亿用科学记数法表示为( )A、 B、 C、 D、3. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、4. 如图,函数和的图象相交于点 , 则不等式的解集为( )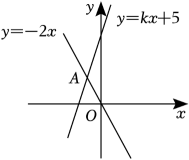 A、 B、 C、 D、5. 如图,直线 , 等边的顶点C在直线b上,若 , 则的度数为( )
A、 B、 C、 D、5. 如图,直线 , 等边的顶点C在直线b上,若 , 则的度数为( ) A、 B、 C、 D、6. 下列说法正确的是( )A、某彩票中奖率是1%,买100张彩票一定有一张中奖 B、从装有10个红球的袋子中摸出一个白球是随机事件 C、篮球巨星姚明在罚球线投篮一次投中是必然事件 D、为了解一批日光灯的使用寿命可采用抽样调查7. 如图,点O为的边上的一点,经过点B且恰好与边相切于点C,若 , , 则阴影部分的面积为( )
A、 B、 C、 D、6. 下列说法正确的是( )A、某彩票中奖率是1%,买100张彩票一定有一张中奖 B、从装有10个红球的袋子中摸出一个白球是随机事件 C、篮球巨星姚明在罚球线投篮一次投中是必然事件 D、为了解一批日光灯的使用寿命可采用抽样调查7. 如图,点O为的边上的一点,经过点B且恰好与边相切于点C,若 , , 则阴影部分的面积为( )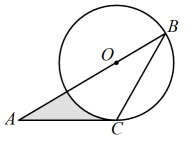 A、 B、 C、 D、8. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是( )
A、 B、 C、 D、8. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是( ) A、 B、6 C、 D、89. 如图,等边内有一点E, , , 当时,则的长为( )
A、 B、6 C、 D、89. 如图,等边内有一点E, , , 当时,则的长为( ) A、2 B、 C、3 D、10. 如图,矩形ABCD中,∠BAC=60°,点E在AB上,且BE:AB=1:3,点F在BC边上运动,以线段EF为斜边在点B的异侧作等腰直角三角形GEF,连接CG,当CG最小时,的值为( )
A、2 B、 C、3 D、10. 如图,矩形ABCD中,∠BAC=60°,点E在AB上,且BE:AB=1:3,点F在BC边上运动,以线段EF为斜边在点B的异侧作等腰直角三角形GEF,连接CG,当CG最小时,的值为( )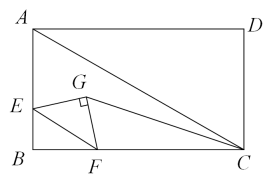 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 有4张背面相同,正面分别印有的卡片,现将这4张卡片背面朝上,从中随机抽取1张,恰好抽到正面印有整数的卡片的概率为 .13. 如图,在中, , 点D是边的中点,过点D作于点M,延长至点E,且 , 连接交于点N,若 , 则的长为 .
 14. 如图,在中, , 在轴上,平分 , 平分 , 与相交于点 , 且 , , 反比例函数的图象经过点 , 则的值为 .
14. 如图,在中, , 在轴上,平分 , 平分 , 与相交于点 , 且 , , 反比例函数的图象经过点 , 则的值为 . 15. 如图,点G是内的一点,且 , 是等边三角形,若 , 则的最大值为 .
15. 如图,点G是内的一点,且 , 是等边三角形,若 , 则的最大值为 .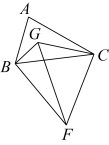
三、解答题
-
16. 化简分式: , 并从1,2,3这三个数中取一个合适的数作为x的值代入求值.17. 如图,已知点 , , 以坐标原点O为位似中心,在第四象限将缩小为原来的三分之一(即新图形与原图形的相似比为).
 (1)、画出缩小后的图形;(2)、写出B点的对应点坐标;(3)、如果内部一点M的坐标为 , 写出点M经位似变换后的对应点坐标.18. 为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中信息,解决下列问题:
(1)、画出缩小后的图形;(2)、写出B点的对应点坐标;(3)、如果内部一点M的坐标为 , 写出点M经位似变换后的对应点坐标.18. 为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中信息,解决下列问题: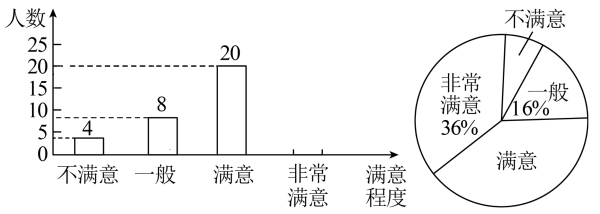 (1)、求此次调查中接受调查的人数,并补全条形统计图.(2)、若本市人口300万人,估算该市对市创卫工作表示满意和非常满意的人数.(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自同区的概率.19. 如图,的弦交于点E,连接 , 延长到点P,连结与相切,且 .
(1)、求此次调查中接受调查的人数,并补全条形统计图.(2)、若本市人口300万人,估算该市对市创卫工作表示满意和非常满意的人数.(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自同区的概率.19. 如图,的弦交于点E,连接 , 延长到点P,连结与相切,且 . (1)、求证:点A是的中点;(2)、若 , , 求的长.20. 铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了元,购进苹果数量是试销时的2倍.(1)、试销时该品种苹果的进货价是每千克多少元?两次共购进多少苹果?(2)、如果超市将该品种苹果按每千克10元的定价出售,当大部分苹果售出后,余下的500千克按定价的六折售完,那么超市在这两次苹果销售中共盈利多少元?21. 在初中阶段的函数学习中,我们经历了“确定函数的表达式,利用函数图象研究其性质,运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.学习了一次函数之后,现在来解决下面的问题:
(1)、求证:点A是的中点;(2)、若 , , 求的长.20. 铭润超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了元,购进苹果数量是试销时的2倍.(1)、试销时该品种苹果的进货价是每千克多少元?两次共购进多少苹果?(2)、如果超市将该品种苹果按每千克10元的定价出售,当大部分苹果售出后,余下的500千克按定价的六折售完,那么超市在这两次苹果销售中共盈利多少元?21. 在初中阶段的函数学习中,我们经历了“确定函数的表达式,利用函数图象研究其性质,运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.学习了一次函数之后,现在来解决下面的问题:在中,下表是y与x的几组对应值.
…
-3
-2
-1
0
1
2
3
…
…
7
3
1
1
3
…
 (1)、 , ;(2)、平面直角坐标系中,画出函数的图象;(3)、根据图象,判断下列关于该函数性质的说法是否符合题意,正确的打√,错误的打×.
(1)、 , ;(2)、平面直角坐标系中,画出函数的图象;(3)、根据图象,判断下列关于该函数性质的说法是否符合题意,正确的打√,错误的打×.①该函数图象是轴对称图形,对称轴为直线 . ( )
②当时,y随x的增大而增大,当时,y随x的增大而减小.( )
③该函数在自变量的取值范围内有最小值,当时有最小值 . ( )
(4)、若方程组有且只有一个公共解,则t的取值范围是 .22. 平行四边形中,点E在边上,连 , 点F在线段上,连 , 连 . (1)、如图1,已知 , 点E为中点, . 若 , 求的长度;(2)、如图2,已知 , 将射线沿翻折交于H,过点C作交于点G.若 , 求证:;(3)、如图3,已知 , 若 , 直接写出的最小值.
(1)、如图1,已知 , 点E为中点, . 若 , 求的长度;(2)、如图2,已知 , 将射线沿翻折交于H,过点C作交于点G.若 , 求证:;(3)、如图3,已知 , 若 , 直接写出的最小值.