广东省梅州市兴宁县2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下列有关实数的运算不一定成立的是( )A、 B、 C、 D、2. 下列有关科学记数法的理解一定正确的是( )A、 B、 C、 D、为整数3. 古语有言“逸一时,误一世”,其意是教导我们青少年要珍惜时光,切勿浪费时间,浪费青春,其数字谐音为1,1,4,5,1,4,有关这一组数,下列说法错误的是( )A、中位数为4.5 B、平均数为 C、众数是1 D、极差是44. 已知实数a,b满足 , 则有关x的不等式组的解集为( )A、 B、 C、 D、无解5. 已知一个正多边形的每个内角是 ,则这个正多边形是( )A、正八边形 B、正十边形 C、正十二边形 D、正十四边形6. 无理数的估值最接近于有理数( )A、0.7 B、0.6 C、0.5 D、0.47. 已知双曲线与双曲线与直线从左到右依次交于四点,若(为坐标原点),则的值为( )A、 B、 C、 D、8. 在小于20的质数中,一次性从中抽出2个,将这两个数作差并取绝对值后得到一个新的数,则这个数仍为质数的概率是( )A、 B、 C、 D、9. 已知抛物线与一次函数交于两点,则线段的长度为( )A、 B、 C、 D、2010. 如题图所示,已知一个半径为2的 , P为平面内一个点,过点P作的两条切线 , , 为的一条直径,且 , 连接若干条线段的端点.若 , 下列给出的四个命题中,为假命题的是( )
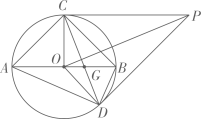 A、 B、为正三角形 C、 D、
A、 B、为正三角形 C、 D、二、填空题
-
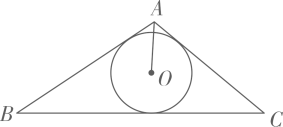
11. 计算: .12. 的展开式中的系数为 .13. 写出一个函数使其图像与反比例函数的图象有3个不同的交点 .14. 一列数 , , , …….满足条件: , , ( , 且n为正整数),则 .15. 如题图所示,在中存在一面积为的内切圆,其圆心为点 , 连接 , 若满足 , , , 则实数的值为 .
三、解答题
-
16. 化简求值: , 其中 , .17. 如题图所示,在四边形中, , , , , 以A为圆心,为半径画弧,交于点E,且该圆弧恰好经过点B,过点E作交于点F.
 (1)、求证:四边形是菱形;(2)、求阴影部分面积.(计算结果保留)18. 在某次高三数学一模考试中,高三(六)班统计了数列大题的得分情况如下表所示,现已知高三(六)班共计50人,本数列大题满分10分,若 .
(1)、求证:四边形是菱形;(2)、求阴影部分面积.(计算结果保留)18. 在某次高三数学一模考试中,高三(六)班统计了数列大题的得分情况如下表所示,现已知高三(六)班共计50人,本数列大题满分10分,若 .得分
0
1
2
3
4
5
6
7
8
9
人数
3
1
3
3
7
2
6
a
6
b
(1)、求实数a,b的值;(2)、求这50名学生的成绩的平均数,众数;(3)、若在该班随机抽取一名学生,该学生得分为5分及5分以下的概率是 .(4)、若该学校共有1200名学生,试估计该学校该题的满分学生的人数.19. 若关于x,y的二元一次方程 , 若满足 , .(1)、求参数a的取值范围;(2)、若y为一个直角三角形的一条直角边长,x为该直角三角形的斜边长,另一条直角边长为方程的一个根,试求该直角三角形的周长.20. 兴宁县有一间名为“韩国料理”的餐饮店,味美价廉,该店以“肥牛鸡排双拼饭”与“鳕鱼肥牛双拼饭”出名,每天吸引附近很多学生慕名而来.现已知“肥牛鸡排双拼饭”单价比“鳕鱼肥牛双拼饭”高5元,且用500元购买“肥牛鸡排双拼饭”与用400元购买“鳕鱼肥牛双拼饭”数量相同.(1)、求“肥牛鸡排双拼饭”与“鳕鱼肥牛双拼饭”的单价;(2)、经过市场调研发现,以(1)中的单价出售“肥牛鸡排双拼饭”每天可以出售80份,若每份售价提高1元时,每天出售份数少3份,设每份售价提高x元且x为整数,y为每天的营业额,求y关于x的函数解析式以及营业额y的最大值.21. 如题图所示,为等腰直角三角形, , 点D为线段上一点,延长至点E使 , 连接 , , 延长交于点F,求证: . 22. 已知二次函数 , 关于x的方程有下列四个命题:①是方程的根 ②是方程的根 ③该方程两根和为4 ④该方程两根同号,若其中只有1个命题为假命题,将向左平移个单位,向下平移个单位得到函数 .
22. 已知二次函数 , 关于x的方程有下列四个命题:①是方程的根 ②是方程的根 ③该方程两根和为4 ④该方程两根同号,若其中只有1个命题为假命题,将向左平移个单位,向下平移个单位得到函数 .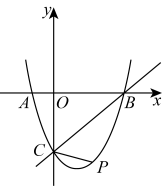 (1)、求函数与的解析式;(2)、如题图所示,已知与x轴相交于A、B两点,与y轴交于点C.点P是抛物线上位于直线BC下方一动点,当时,求点P的坐标;23. 在平面直角坐标系中,有一矩形 , 连接、 , 已知点B的坐标为 .
(1)、求函数与的解析式;(2)、如题图所示,已知与x轴相交于A、B两点,与y轴交于点C.点P是抛物线上位于直线BC下方一动点,当时,求点P的坐标;23. 在平面直角坐标系中,有一矩形 , 连接、 , 已知点B的坐标为 .ⅰ:如题图1所示,反比例函数 , 点P为反比例函数上一动点,设 .
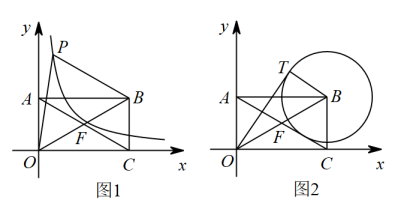 (1)、连接 , , 当时,求与t的函数关系式;(2)、若点P满足 , 求满足该条件的P点个数;
(1)、连接 , , 当时,求与t的函数关系式;(2)、若点P满足 , 求满足该条件的P点个数;ⅱ:如题图2所示,以点B为圆心,作一个与AC相切的 , 过点O作的切线,切点T位于左上方;
(3)、试问直线与直线是否垂直,若垂直,请给出证明:若不垂直,请说明理由.