广东省惠州市惠东县2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 据统计,2022年全国新冠病毒疫苗及接种费用1500余亿元,将数据1500亿用科学记数法表示为( )A、 B、 C、 D、3. 下列运算错误的是( )A、 B、 C、 D、4. 如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
2. 据统计,2022年全国新冠病毒疫苗及接种费用1500余亿元,将数据1500亿用科学记数法表示为( )A、 B、 C、 D、3. 下列运算错误的是( )A、 B、 C、 D、4. 如图是由6个完全相同的小正方体组成的几何体,其俯视图为( ) A、
A、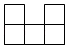 B、
B、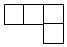 C、
C、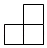 D、
D、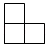 5. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,则本次比赛共有参赛队伍( )A、8支 B、9支 C、10支 D、11支6. 数据2,4,8,5,3,5,5,4的众数、中位数分别为( )A、4.5、5 B、5、4.5 C、5、4 D、5、57. 关于x的一元二次方程的一个根是0,则a的值为( )A、1 B、1或-1 C、-1 D、0.58. 如图,平行四边形的对角线、相交于点O,E是的中点,若的面积为1,则的面积为( )
5. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,则本次比赛共有参赛队伍( )A、8支 B、9支 C、10支 D、11支6. 数据2,4,8,5,3,5,5,4的众数、中位数分别为( )A、4.5、5 B、5、4.5 C、5、4 D、5、57. 关于x的一元二次方程的一个根是0,则a的值为( )A、1 B、1或-1 C、-1 D、0.58. 如图,平行四边形的对角线、相交于点O,E是的中点,若的面积为1,则的面积为( )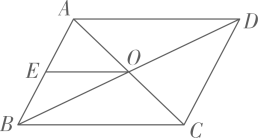 A、2 B、3 C、4 D、59. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A、2 B、3 C、4 D、59. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )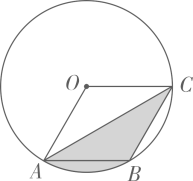 A、6π B、π C、π D、2π10. 如图,等边的边长为4 cm,点P,点Q同时从点A出发点,Q沿AC以1cm/s的速度向点C运动,点P沿A—B—C以2 cm/s的速度也向点C运动,直到到达点C时停止运动,若的面积为S(单位:),点Q的运动时间为t(单位:s),则下列最能反映S与t之间关系的大致图象是( )
A、6π B、π C、π D、2π10. 如图,等边的边长为4 cm,点P,点Q同时从点A出发点,Q沿AC以1cm/s的速度向点C运动,点P沿A—B—C以2 cm/s的速度也向点C运动,直到到达点C时停止运动,若的面积为S(单位:),点Q的运动时间为t(单位:s),则下列最能反映S与t之间关系的大致图象是( ) A、
A、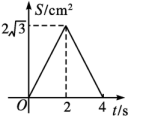 B、
B、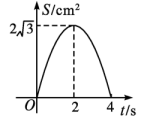 C、
C、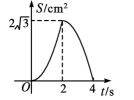 D、
D、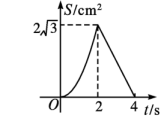
二、填空题
-
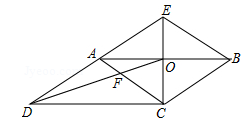
11. 二元一次方程组的解是.12. 已知一个n边形的内角和等于720°,则n= .13. 将抛物线向上平移2个单位,那么所得新抛物线的表达式是 .14. 已知 , 则代数式的值为.15. 如图,CE是▱ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有 . (填写所有正确结论的序号)
三、解答题
-
16. 计算: .17. 先化简,再求值: , 其中 .18. 如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF.
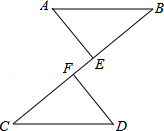 (1)、求证:△ABE≌△DCF;(2)、试证明:以A、F、D、E为顶点的四边形是平行四边形.19. 以“赏中华诗词、寻文化基因,品生活之美”为基本宗旨的《中国诗词大会》是央视首档全民参与的诗词节目.某语文科组对本校学生了解《中国诗词大会》的情况进行调查,随机选取部分学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):.几乎每期都看;.看过几期;听说过,但没看过;没听说过,现绘制了如图的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)、求证:△ABE≌△DCF;(2)、试证明:以A、F、D、E为顶点的四边形是平行四边形.19. 以“赏中华诗词、寻文化基因,品生活之美”为基本宗旨的《中国诗词大会》是央视首档全民参与的诗词节目.某语文科组对本校学生了解《中国诗词大会》的情况进行调查,随机选取部分学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):.几乎每期都看;.看过几期;听说过,但没看过;没听说过,现绘制了如图的条形统计图和扇形统计图,请结合统计图回答下列问题: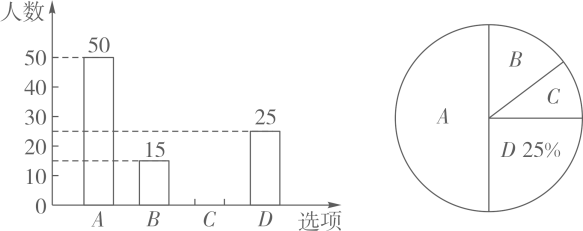 (1)、本次共问卷调查名学生:扇形统计图中,选项对应的扇形圆心角是度.(2)、补全图中的条形统计图.(3)、该校选“”的学生中有甲、乙、丙三人最关注该节目,学校决定从这三名学生中随机抽取两名为该节目作宣传,用列表法或画树状图法求同时抽到甲、乙两名学生的概率.20. 因疫情防控的需要,某小学购买儿童医用口罩和成人医用口罩以满足全体师生的需要,其中这两种口罩每包所装的片数相同,每包成人医用口罩的价格比每包儿童医用口罩的价格少4元,用1200元购买儿童口罩的包数恰好是同样的钱购买成人口罩的包数 .(1)、求成人医用口罩和儿童医用口罩每包的价格分别是多少元?(2)、若购买这两种口罩共120包,要求儿童口罩的包数不少于成人口罩包数的3倍.请设计一种购买方案,使所需总费用最低.21. 如图,直线与双曲线交于、两点,且点的坐标为 .
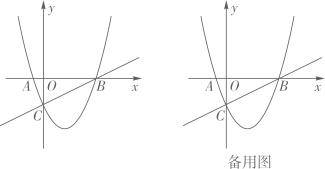
(1)、本次共问卷调查名学生:扇形统计图中,选项对应的扇形圆心角是度.(2)、补全图中的条形统计图.(3)、该校选“”的学生中有甲、乙、丙三人最关注该节目,学校决定从这三名学生中随机抽取两名为该节目作宣传,用列表法或画树状图法求同时抽到甲、乙两名学生的概率.20. 因疫情防控的需要,某小学购买儿童医用口罩和成人医用口罩以满足全体师生的需要,其中这两种口罩每包所装的片数相同,每包成人医用口罩的价格比每包儿童医用口罩的价格少4元,用1200元购买儿童口罩的包数恰好是同样的钱购买成人口罩的包数 .(1)、求成人医用口罩和儿童医用口罩每包的价格分别是多少元?(2)、若购买这两种口罩共120包,要求儿童口罩的包数不少于成人口罩包数的3倍.请设计一种购买方案,使所需总费用最低.21. 如图,直线与双曲线交于、两点,且点的坐标为 .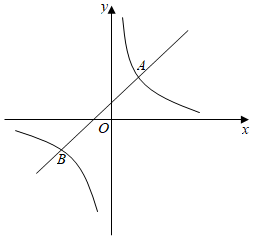 (1)、求双曲线与直线的解析式;(2)、求点的坐标;(3)、若 , 直接写出的取值范围.
(1)、求双曲线与直线的解析式;(2)、求点的坐标;(3)、若 , 直接写出的取值范围.