广东省广州市荔湾区2023年中考一模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 中国是最早采用正负数表示相反意义的量的国家.如果将“收入60元”记作“+60元”,那么“支出40元”记作( )A、+40元 B、-40元 C、+20元 D、-20元2. 在平面直角坐标系中,将点向右平移5个单位得到的点的坐标为( )A、 B、 C、 D、3. 一组数据2,3,4,2,5的众数和中位数分别是( )A、2,2 B、2,3 C、2,4 D、5,44. 下列运算正确的是( )A、 B、 C、 D、5. 在中, , , 则的值是( )A、 B、 C、 D、6. 我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步,问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x人,y辆车,则可列方程组为( )A、 B、 C、 D、7. 如图,将绕点A逆时针旋转得到 , 若且于点 , 则的度数为( )
 A、 B、 C、 D、8. 如图是一个几何体的三视图,主视图和左视图均是面积为12的等腰三角形,俯视图是直径为6的圆,则这个几何体的全面积是( )
A、 B、 C、 D、8. 如图是一个几何体的三视图,主视图和左视图均是面积为12的等腰三角形,俯视图是直径为6的圆,则这个几何体的全面积是( ) A、 B、 C、 D、9. 如图,函数 和 的图象相交于点 ,则不等式 的解集为( )
A、 B、 C、 D、9. 如图,函数 和 的图象相交于点 ,则不等式 的解集为( )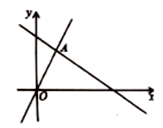 A、 B、 C、 D、10. 已知方程的两根分别为 , , 则的值为( ).A、1 B、2023 C、-1 D、-2023
A、 B、 C、 D、10. 已知方程的两根分别为 , , 则的值为( ).A、1 B、2023 C、-1 D、-2023二、填空题
-
11. 计算: .12. 分解因式:9a3﹣ab2= .
13. 已知抛物线与x轴仅有一个公共点,则m的值为 .14. 已知直线向下平移个单位后经过点 , 则的值为 .15. 如图,是的弦,交于点P,过点B的直线交的延长线于点C,若 , , , 则的长为 . 16. 如图,Rt△ABC中,∠ACB=90°,AC=2,BC=4,CD是△ABC的中线,E是边BC上一动点,将△BED沿ED折叠,点B落在点F处,EF交线段CD于点G,当△DFG是直角三角形时,则CE=.
16. 如图,Rt△ABC中,∠ACB=90°,AC=2,BC=4,CD是△ABC的中线,E是边BC上一动点,将△BED沿ED折叠,点B落在点F处,EF交线段CD于点G,当△DFG是直角三角形时,则CE=.
三、解答题
-
17. 解不等式 , 并把解集在数轴上表示出来.
 18. 如图,在四边形中, , , 连接 . 求证: .
18. 如图,在四边形中, , , 连接 . 求证: . 19. 已知 .(1)、化简;(2)、若 , 是菱形两条对角线的长,且该菱形的面积为 , 求的值.20. 北京冬奥会期间,学校为了解学生最喜欢的冰雪运动,从全校随机抽取了部分学生进行了问卷调查,每个被调查的学生从滑雪、滑冰、冰球、冰壶这4种冰雪运动中选择最喜欢的一项.该小组将调查数据进行整理并绘制成如下两幅不完整的统计图.
19. 已知 .(1)、化简;(2)、若 , 是菱形两条对角线的长,且该菱形的面积为 , 求的值.20. 北京冬奥会期间,学校为了解学生最喜欢的冰雪运动,从全校随机抽取了部分学生进行了问卷调查,每个被调查的学生从滑雪、滑冰、冰球、冰壶这4种冰雪运动中选择最喜欢的一项.该小组将调查数据进行整理并绘制成如下两幅不完整的统计图. (1)、这次调查中,一共调查了 ▲ 名学生,请补全条形统计图;(2)、若全校有2600名学生,则估计该校最喜欢“滑冰”运动项目的有名学生;(3)、已知选冰壶的4名学生中1名来自七年级,1名来自八年级,2名来自九年级,学校想要从这4名学生中随机抽取2名学生进行访谈.请用画树状图或列表法求抽到的2名学生来自不同年级的概率.21. 班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:(1)、大巴与小车的平均速度各是多少?(2)、苏老师追上大巴的地点到基地的路程有多远?22. 如图,在平面直角坐标系中,矩形的顶点在轴的正半轴上,.对角线相交于点 , 反比例函数的图像经过点 , 分别与交于点.
(1)、这次调查中,一共调查了 ▲ 名学生,请补全条形统计图;(2)、若全校有2600名学生,则估计该校最喜欢“滑冰”运动项目的有名学生;(3)、已知选冰壶的4名学生中1名来自七年级,1名来自八年级,2名来自九年级,学校想要从这4名学生中随机抽取2名学生进行访谈.请用画树状图或列表法求抽到的2名学生来自不同年级的概率.21. 班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:(1)、大巴与小车的平均速度各是多少?(2)、苏老师追上大巴的地点到基地的路程有多远?22. 如图,在平面直角坐标系中,矩形的顶点在轴的正半轴上,.对角线相交于点 , 反比例函数的图像经过点 , 分别与交于点. (1)、若 , 求的值;(2)、连接 , 若 , 求的面积.23. 如图,是的外接圆, , 是的切线.
(1)、若 , 求的值;(2)、连接 , 若 , 求的面积.23. 如图,是的外接圆, , 是的切线. (1)、尺规作图:过点B作的平行线交于点E,交于点F,连接(保留作图痕迹,不写作法);(2)、证明:;(3)、若的半径长为 , , 求和的长.
(1)、尺规作图:过点B作的平行线交于点E,交于点F,连接(保留作图痕迹,不写作法);(2)、证明:;(3)、若的半径长为 , , 求和的长.
