广东省广州市花都区2023年中考数学一模试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 在﹣1,﹣5,3,0这四个数中,最小的数是( )A、﹣1 B、﹣5 C、3 D、02. 下面四个几何体中,从正面看是三角形的是( )A、
 B、
B、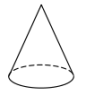 C、
C、 D、
D、 3. 激昂奋进新时代,推进中国式现代化,2023年全国两会公布了2022年国内生产总值,近五年国内生产总值呈逐年上升趋势,分别为91,99,101,114,121(单位:万亿),这五个数据的中位数是( )A、91 B、99 C、101 D、1214. 下列运算中,正确的是( )A、 B、 C、 D、5. 如图,在中, , 则的度数为( )
3. 激昂奋进新时代,推进中国式现代化,2023年全国两会公布了2022年国内生产总值,近五年国内生产总值呈逐年上升趋势,分别为91,99,101,114,121(单位:万亿),这五个数据的中位数是( )A、91 B、99 C、101 D、1214. 下列运算中,正确的是( )A、 B、 C、 D、5. 如图,在中, , 则的度数为( ) A、 B、 C、 D、6. 对于一次函数 , 下列说法错误的是( )A、随的增大而减小 B、图象与轴交点为 C、图象经过第一、二、四象限 D、图象经过点7. 如图,一枚运载火箭从地面L处发射,雷达站R与发射点L距离 , 当火箭到达A点时,雷达站测得仰角为 , 则这枚火箭此时的高度为( )
A、 B、 C、 D、6. 对于一次函数 , 下列说法错误的是( )A、随的增大而减小 B、图象与轴交点为 C、图象经过第一、二、四象限 D、图象经过点7. 如图,一枚运载火箭从地面L处发射,雷达站R与发射点L距离 , 当火箭到达A点时,雷达站测得仰角为 , 则这枚火箭此时的高度为( ) A、 B、 C、 D、8. 已知关于x的一元二次方程无实数根,则抛物线的顶点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,三个边长分别为2,4,6的菱形如图所示拼叠,则线段的长度为( )
A、 B、 C、 D、8. 已知关于x的一元二次方程无实数根,则抛物线的顶点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,三个边长分别为2,4,6的菱形如图所示拼叠,则线段的长度为( ) A、 B、 C、 D、110. 如图,在平面直角坐标系中,点 , 点从出发,以每秒1个单位长度的速度沿折线运动了秒,直线上有一动点 , 轴上有一动点 , 当的和最小时,点的坐标为( )
A、 B、 C、 D、110. 如图,在平面直角坐标系中,点 , 点从出发,以每秒1个单位长度的速度沿折线运动了秒,直线上有一动点 , 轴上有一动点 , 当的和最小时,点的坐标为( )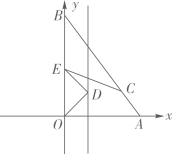 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, , 则的度数为 .
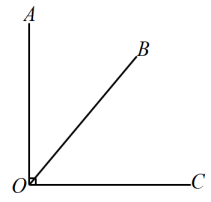 12. 计算: =
12. 计算: =
13. 方程的解为 .14. 物理学中,在压力F不变的情况下,某物体承受的压强p与它的受力面积S成反比例函数关系,则下表中压强与的大小关系为: . (填“”,“”或“”)1
2
3
300
15. 一副三角板如图摆放,点为中点,连结 , 将三角板绕点顺时针旋转角度 , 使得 , 则的度数为 . 16. 如图,边长为1的正方形中,点E为边上动点(不与A、D重合),连接 , 将沿折叠得到 , 延长交于点F,连接 , 交于点N,连接 . 则下列结论:①;②的周长是定值2;③当点E是中点时,;④点D到距离的最大值为 , 其中正确的结论有(填写所有正确结论的序号).
16. 如图,边长为1的正方形中,点E为边上动点(不与A、D重合),连接 , 将沿折叠得到 , 延长交于点F,连接 , 交于点N,连接 . 则下列结论:①;②的周长是定值2;③当点E是中点时,;④点D到距离的最大值为 , 其中正确的结论有(填写所有正确结论的序号).
三、解答题
-
17. 解方程组:18. 如图,在矩形中,点为的中点,连接和 , 求证: .
 19. 已知: .(1)、化简P;(2)、当a满足不等式组且a为整数时,求P的值.20. 为振兴乡村文化,某社区准备开展“乡村文化宣讲”活动,为了更好的开展活动,该社区随机抽取部分居民,调查他们对乡村文化的了解情况.根据调查结果,把居民对乡村文化的了解程度分为“ . 非常了解”“ . 比较了解”“ . 有点了解”“ . 不了解”四个层次,并依据调查结果绘制了如图所示的两幅不完整的统计图.
19. 已知: .(1)、化简P;(2)、当a满足不等式组且a为整数时,求P的值.20. 为振兴乡村文化,某社区准备开展“乡村文化宣讲”活动,为了更好的开展活动,该社区随机抽取部分居民,调查他们对乡村文化的了解情况.根据调查结果,把居民对乡村文化的了解程度分为“ . 非常了解”“ . 比较了解”“ . 有点了解”“ . 不了解”四个层次,并依据调查结果绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)、这次共抽取了位居民进行调查;扇形统计图中,“”层次所占圆心角的度数是 .(2)、现拟从“非常了解”乡村文化的甲、乙、丙、丁四位居民中任选2位担任乡村文化推广使者,请用列举法求恰好选中甲、乙两位居民的概率.21. “桃之夭夭,灼灼其华”,每年月份,我区某湿地公园内的桃花陆续绽放,引来众多市民前往踏青观赏,纷纷拍照留念,记录生活美好时光,小王抓住这一商机,计划从市场购进、两种型号的手机自拍杆进行销售,据调查,购进1件型号和1件型号自拍杆共需45元,其中1件型号自拍杆价格是1件型号自拍杆价格的2倍.(1)、求1件型号和1件型号自拍杆的进价各是多少元?(2)、若小王计划购进、两种型号自拍杆共100件,并将这两款手机自拍杆分别以20元,50元的价钱进行售卖,为了保证全部售卖完后的总利润不低于1100元,求最多购进型号自拍杆多少件?22. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点 , 与x轴、y轴分别交于点B、C.过点A作轴,垂足为D. (1)、求反比例函数的表达式;(2)、点P为反比例函数图象上的一点,且位于点A的右侧,从条件①或者条件②这两个条件中选择一个作为已知条件,求点P的坐标.
(1)、求反比例函数的表达式;(2)、点P为反比例函数图象上的一点,且位于点A的右侧,从条件①或者条件②这两个条件中选择一个作为已知条件,求点P的坐标.条件①:;条件②:面积是面积的2倍.
注明:如果选择条件①与条件②分别作答,按第一个解答计分.
23. 如图,是的外接圆,直径平分交于点E. (1)、尺规作图:在的延长线上取一点F,使得 , 连接;(保留作图痕迹,不写作法)(2)、在(1)所作的图中:
(1)、尺规作图:在的延长线上取一点F,使得 , 连接;(保留作图痕迹,不写作法)(2)、在(1)所作的图中:①证明:是的切线;
②求的值.
