安徽省合肥市庐江县2023年中考二模数学试题
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下面四个数中,最小的数是( )A、-2 B、1 C、 D、2. 我国倡导的“一带一路”建设覆盖总人口约为44亿人,44亿用科学记数法表示为( )A、 B、 C、 D、3. 某商品月份单个的进价和售价如图所示,则售出该商品单个利润最大的是( )
 A、1月 B、2月 C、3月 D、4月4. 一个长方体截去一个小长方体得到的一个形几何体如图水平放置,则其左视图是( )
A、1月 B、2月 C、3月 D、4月4. 一个长方体截去一个小长方体得到的一个形几何体如图水平放置,则其左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列各式计算正确的是( )A、 B、 C、 D、6. 如图,将一张矩形纸片折叠,若∠1=78°,则∠2的度数是( )
5. 下列各式计算正确的是( )A、 B、 C、 D、6. 如图,将一张矩形纸片折叠,若∠1=78°,则∠2的度数是( )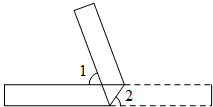 A、51° B、56° C、61° D、78°7. 如图,点C,D在上,直径且 , 则弧的长为( )
A、51° B、56° C、61° D、78°7. 如图,点C,D在上,直径且 , 则弧的长为( ) A、 B、 C、 D、8. 某校九年级一班准备举行一次演讲比赛,甲、乙、丙三人通过抽签的方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率为( )A、 B、 C、 D、9. 已知一次函数(为常数)的图象如图所示,则函数的图象是( )
A、 B、 C、 D、8. 某校九年级一班准备举行一次演讲比赛,甲、乙、丙三人通过抽签的方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率为( )A、 B、 C、 D、9. 已知一次函数(为常数)的图象如图所示,则函数的图象是( ) A、
A、 B、
B、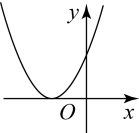 C、
C、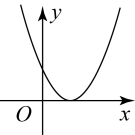 D、
D、 10. 如图, , , 点 , 分别在 , 的另一边上运动,并保持2,点在边上, , 点是的中点,若点为上任意一点,则的最小值为( )
10. 如图, , , 点 , 分别在 , 的另一边上运动,并保持2,点在边上, , 点是的中点,若点为上任意一点,则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 分解因式: .13. 如图, , , 将向右平移到位置A的对应点是 , 的对应点是 , 反比例函数的图象经过点和的中点 , 则的值是 .
 14. 如图,在正方形中,点、分别在边、上,且 , 交于点,交于点.
14. 如图,在正方形中,点、分别在边、上,且 , 交于点,交于点. (1)、若正方形的边长为2,则的周长是 .(2)、若 , 则 .
(1)、若正方形的边长为2,则的周长是 .(2)、若 , 则 .三、解答题
-
15. 解不等式: .16. 如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点).

⑴将向右平移6个单位长度,再向下平移5个单位长度,画出平移后的图形为;
⑵画出绕A点顺时针方向旋转后的图形为 .
17. 为了丰富同学们的课余生活、拓展同学们的视野,学校书店准备购进甲、乙两类中学生书刊,已知甲类书刊比乙类书刊每本贵2元,若购买500本甲类书刊和400本乙类书刊共需要8200元,其中甲、乙两类书刊的进价和售价如表:甲
乙
进价/(元/本)
售价/(元/本)
20
13
(1)、求 , 的值;(2)、第二次小卖部购进了1000本甲书刊和500本乙书刊,为了扩大销量,小卖部准备对甲书刊进行打折出售,乙书刊价格不变,全部售完后总利润为8500元,求甲书刊打了几折?18. 观察下列图形和其对应的等式:
根据以上规律,解决下列问题:
(1)、写出第5个图形对应的等式是 .(2)、第个图形对应的等式是 ▲ (用含的等式表示),并证明.19. 如图,点是直径延长线上一点, , 点是上一个动点(不与点 , 重合),点为半径的中点. (1)、如图1,若 , 求的长;(2)、如图2,当时,求证:是的切线.20. 为响应二十大新型城镇化战略,助力乡村振兴,某县计划在乡镇之间增设燃气管道.如图,同一平面上的四个点 , , , 为某县四个乡镇的中心点, , 两个乡镇之间已铺设燃气主管道 , 其长为27千米.计划在 , 两个乡镇之间再铺设燃气主管道 . 已知 , , . 求的长.(结果保留整数,参考数据: , , , )
(1)、如图1,若 , 求的长;(2)、如图2,当时,求证:是的切线.20. 为响应二十大新型城镇化战略,助力乡村振兴,某县计划在乡镇之间增设燃气管道.如图,同一平面上的四个点 , , , 为某县四个乡镇的中心点, , 两个乡镇之间已铺设燃气主管道 , 其长为27千米.计划在 , 两个乡镇之间再铺设燃气主管道 . 已知 , , . 求的长.(结果保留整数,参考数据: , , , ) 21. 某学校为了解学生的身高情况,各年级分别抽样调查了部分同学的身高,并分年级对所得数据进行处理.下面的频数分布直方图(部分)和扇形统计图是根据七年级的调查数据制作而成.(每组含最低值不含最高值,身高单位: , 测量时精确到):
21. 某学校为了解学生的身高情况,各年级分别抽样调查了部分同学的身高,并分年级对所得数据进行处理.下面的频数分布直方图(部分)和扇形统计图是根据七年级的调查数据制作而成.(每组含最低值不含最高值,身高单位: , 测量时精确到):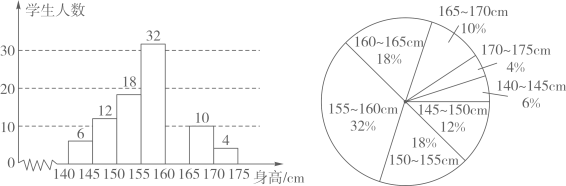 (1)、请根据以上信息,完成下列问题:
(1)、请根据以上信息,完成下列问题:①七年级身高在的学生有 ▲ 人;
②七年级样本的中位数所在范围是 ▲ , 请说明理由;
(2)、已知七年级共有名学生,若身高低于 , 则认定该学生身高偏矮.请估计该校七年级身高偏矮的共有多少人,并说明理由.(3)、体育组对抽查的数据进行分析,计算出各年级的平均身高及方差如下表所示:年级
七
八
九
157
160
169
0.8
0.6
0.9
那么学生的身高比较整齐是哪个年级?为什么.

