安徽省亳州市2023年中考一检数学试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 计算的值( )A、3 B、1 C、 D、2. 如果 , 则下列式子正确的是( )A、 B、 C、 D、3. 点在反比例函数图象上,则下列各点在此函数图象上的是( )A、 B、 C、 D、4. 下列抛物线中,与抛物线具有相同对称轴的是( )A、 B、 C、 D、5. 如图,是的高.若 , , 则边的长为( )
 A、 B、 C、 D、6. 如图, , 若 , , , 则的长是( )
A、 B、 C、 D、6. 如图, , 若 , , , 则的长是( ) A、 B、1 C、2 D、37. 如图,已知点A为反比例函数的图象上一点,过点A作轴,垂足为B,若的面积为1,则k的值为( )
A、 B、1 C、2 D、37. 如图,已知点A为反比例函数的图象上一点,过点A作轴,垂足为B,若的面积为1,则k的值为( )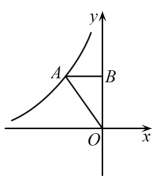 A、1 B、-1 C、2 D、-28. 如图,四边形为菱形, , 交于点O,E是的中点,连接并延长交于点F.已知 , 则的长为( )
A、1 B、-1 C、2 D、-28. 如图,四边形为菱形, , 交于点O,E是的中点,连接并延长交于点F.已知 , 则的长为( )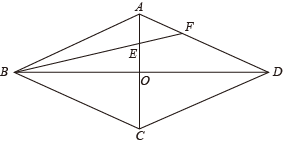 A、 B、1 C、 D、9. 已知: , 且 , 则二次函数的图象可能是下列图象中的( )A、
A、 B、1 C、 D、9. 已知: , 且 , 则二次函数的图象可能是下列图象中的( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在矩形ABCD中, , , 点P从点A出发,按A→B→C的方向在边AB和BC上移动.记 , 点D到直线PA的距离为y,则y的最小值是( )
10. 如图,在矩形ABCD中, , , 点P从点A出发,按A→B→C的方向在边AB和BC上移动.记 , 点D到直线PA的距离为y,则y的最小值是( )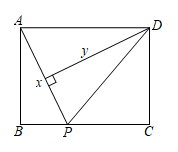 A、6 B、 C、5 D、4
A、6 B、 C、5 D、4二、填空题
-
11. 二次函数的图象经过原点,则a的值为 .12. 如图,点P把线段分成两部分,且为与的比例中项.如果 , 那么 .
 13. 如图,已知的三个顶点均在格点上,则 .
13. 如图,已知的三个顶点均在格点上,则 . 14. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P是边AB上的一点,MN是线段CP的垂直平分线且分别交AC,BC于点M,N.
14. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P是边AB上的一点,MN是线段CP的垂直平分线且分别交AC,BC于点M,N. (1)、若MN∥AB,则MN=;(2)、若MN经过Rt△ABC的某一顶点,则MN= .
(1)、若MN∥AB,则MN=;(2)、若MN经过Rt△ABC的某一顶点,则MN= .三、解答题
-
15. 计算: .16. 如图,在平面直角坐标系中,各顶点的坐标分别为 , , .
 (1)、以坐标原点O为位似中心,在x轴上方作与的位似比为2的位似图形;(2)、直接写出顶点的坐标为 , .17. 已知二次函数中的x和y满足下表:
(1)、以坐标原点O为位似中心,在x轴上方作与的位似比为2的位似图形;(2)、直接写出顶点的坐标为 , .17. 已知二次函数中的x和y满足下表:x
⋯
-4
-3
-2
-1
0
1
2
⋯
y
⋯
-5
0
3
4
3
m
-5
⋯
(1)、根据表格,直接写出该二次函数的对称轴以及m的值;(2)、求该二次函数的表达式.18. 如图,一次函数与反比例函数的图象交于点 , , 与x轴交于点D,与y轴交于点C. (1)、求m,n的值;(2)、观察函数图象,直接写出不等式的解集:_ .19. 如图,在中,C,D分别是上的点.若 .
(1)、求m,n的值;(2)、观察函数图象,直接写出不等式的解集:_ .19. 如图,在中,C,D分别是上的点.若 . (1)、求证:;(2)、求的长.20. 近年来我国无人机设备发展迅猛,新型号无人机不断面世,科研单位为保障无人机设备能安全投产,现针对某种型号的无人机的降落情况进行测试,该型号无人机在跑道起点处着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间满足二次函数关系,其部分函数图象如图所示.
(1)、求证:;(2)、求的长.20. 近年来我国无人机设备发展迅猛,新型号无人机不断面世,科研单位为保障无人机设备能安全投产,现针对某种型号的无人机的降落情况进行测试,该型号无人机在跑道起点处着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间满足二次函数关系,其部分函数图象如图所示. (1)、求y关于x的函数关系式;(2)、若跑道长度为900(m),是否够此无人机安全着陆?请说明理由.21. 体温检测是疫情防控中的一项重要工作,某公司设计了一款红外线体温检测仪,该设备通过探测人体红外辐射的能量对进入测温区域的人员进行快速体温检测.如图,是水平地面,其中是测温区域,测温仪安装在竖直标杆上的点D处,若该测温仪能识别体温的最大张角为(即),能识别体温的最小张角为(即)
(1)、求y关于x的函数关系式;(2)、若跑道长度为900(m),是否够此无人机安全着陆?请说明理由.21. 体温检测是疫情防控中的一项重要工作,某公司设计了一款红外线体温检测仪,该设备通过探测人体红外辐射的能量对进入测温区域的人员进行快速体温检测.如图,是水平地面,其中是测温区域,测温仪安装在竖直标杆上的点D处,若该测温仪能识别体温的最大张角为(即),能识别体温的最小张角为(即)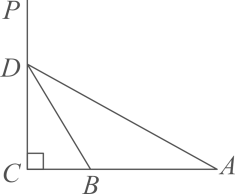 (1)、当设备安装高度为2米时,求测温区域的长度;(结果保留根号)(2)、为了达到良好的检到效果,该公司要求测温区的长不低于3.6米,则设备的最低安装高度约是米.(结果保留1位小数,参考数据: , )
(1)、当设备安装高度为2米时,求测温区域的长度;(结果保留根号)(2)、为了达到良好的检到效果,该公司要求测温区的长不低于3.6米,则设备的最低安装高度约是米.(结果保留1位小数,参考数据: , )

