安徽省2023年百校联赢名校大联考一模数学试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
1. 下列为负数的是( )A、 B、 C、0 D、-12. 一根直尺和一个角的三角板按如图方式叠合在一起,若 , 则的度数是( )
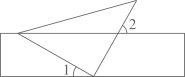 A、 B、 C、 D、3. 2022年全国粮食总产量约13700亿斤,比上年增加73.6亿斤,这里“13700亿”用科学记数法表示为( )A、 B、 C、 D、4. 如图是某几何体的三视图,该几何体是( )
A、 B、 C、 D、3. 2022年全国粮食总产量约13700亿斤,比上年增加73.6亿斤,这里“13700亿”用科学记数法表示为( )A、 B、 C、 D、4. 如图是某几何体的三视图,该几何体是( )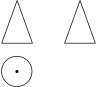 A、
A、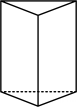 B、
B、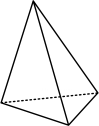 C、
C、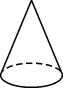 D、
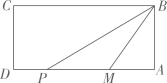
D、 5. 估计的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间6. 某人在甲、乙、丙、丁四个超市购买某品牌商品的总价和购买数量如图所示,按平均单价计算,购买该品牌商品最划算的超市是( )
5. 估计的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间6. 某人在甲、乙、丙、丁四个超市购买某品牌商品的总价和购买数量如图所示,按平均单价计算,购买该品牌商品最划算的超市是( ) A、甲 B、乙 C、丙 D、丁7. 如图,菱形的对角线、相交于点O,过点D作于点H,连接 , 点M是边的中点,连接 , 若 , 菱形的面积为48,则的值为( )
A、甲 B、乙 C、丙 D、丁7. 如图,菱形的对角线、相交于点O,过点D作于点H,连接 , 点M是边的中点,连接 , 若 , 菱形的面积为48,则的值为( )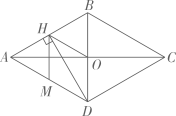 A、 B、 C、 D、8. 在3×3网格中,把2个小正方形涂上灰色,把2个小正方形涂上黑色,如图,现在把剩下的小正方形中的一个小正方形涂上黑色,则正好能组成轴对称图形的概率是( )
A、 B、 C、 D、8. 在3×3网格中,把2个小正方形涂上灰色,把2个小正方形涂上黑色,如图,现在把剩下的小正方形中的一个小正方形涂上黑色,则正好能组成轴对称图形的概率是( ) A、 B、 C、 D、9. 如图,在中, , 点D在斜边上,连接 , 且 , 以点A为圆心,以长为半径作弧交于点E,连接 , 取的中点F,连接 . 下列结论中错误的是( )
A、 B、 C、 D、9. 如图,在中, , 点D在斜边上,连接 , 且 , 以点A为圆心,以长为半径作弧交于点E,连接 , 取的中点F,连接 . 下列结论中错误的是( )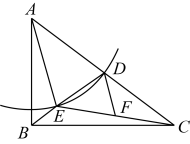 A、平分 B、 C、若 , 则 D、若 , 则10. 如图,中, , , , 点D是边上一动点(不与点A,B重合),过点D作交于点E,点P在边上,连接 , 若 , 的面积为y,则下列最能反映y与x之间函数关系的图象是( )
A、平分 B、 C、若 , 则 D、若 , 则10. 如图,中, , , , 点D是边上一动点(不与点A,B重合),过点D作交于点E,点P在边上,连接 , 若 , 的面积为y,则下列最能反映y与x之间函数关系的图象是( ) A、
A、 B、
B、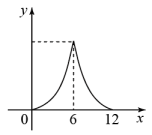 C、
C、 D、
D、
二、填空题
-
11. 计算 .12. 如图,四边形的对角线 , 相交于点O,若 , , 想要判断四边形是菱形,则可以添加一个条件是 .
 13. 如图,中, , , , 以为直径的交于点 , 则的长为 .
13. 如图,中, , , , 以为直径的交于点 , 则的长为 . 14. 已知二次函数(a是常数,且).(1)、该二次函数图象的对称轴是;(2)、该二次函数图象与y轴交点的纵坐标的最大值为 .
14. 已知二次函数(a是常数,且).(1)、该二次函数图象的对称轴是;(2)、该二次函数图象与y轴交点的纵坐标的最大值为 .三、解答题
-
15. 先化简,后求值: , 其中 .16. 如图,在边长为1个单位长度的小正方形组成网格中,的顶点为格点(网格线的交点),直线l经过格点.

⑴画出关于直线l成轴对称的 .
⑵将先向下平移3个单位,再向右平移2个单位得到 , 请画出 .
17. 如图,为了测量东西走向的公路桥梁的长度,数学兴趣小组在公路桥南侧选定观测点C,测得A在C北偏西方向上,点B在C的北偏东方向上,若测得米.求公路桥梁的长(精确到1米).(参考数据 , , ).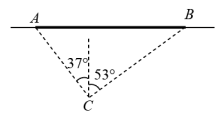 18. 观察以下等式:
18. 观察以下等式:第1个等式;第2个等式;
第3个等式;第4个等式;……
按照以上规律,解决下列问题:
(1)、写出第5个等式:;(2)、写出你猜想的第n个等式(用含n的式子表示),并证明.19. 点P在外,点A,C在上,连接分别交于点B,D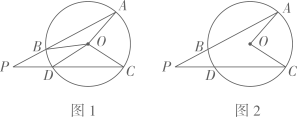 (1)、如图1,若 , , 求的度数;(2)、如图2,若 , 求证: .20. 已知,反比例函数和反比例函数如图所示.
(1)、如图1,若 , , 求的度数;(2)、如图2,若 , 求证: .20. 已知,反比例函数和反比例函数如图所示.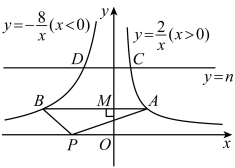 (1)、点A在反比例函数的图象上,过点A作y轴的垂线交反比例函数的图象于点B,交y轴于点M,点P在x轴上,连接 , 求的面积;(2)、直线交反比例函数的图象于点C,交反比例函数的图象于点D,若 , 求n的值.21. 每年的12月4日是我国的“宪法宣传日”,某中学都会在这一天举行宪法知识竞赛,并随机抽取了部分学生的竞赛成绩(优秀:85~100分;良好:70~84分;合格:60~69分;不合格:59分以下)进行调查,将所得数据进行分类,统计绘制了如下不完整的统计图.请根据图中的信息,解答下列问题:
(1)、点A在反比例函数的图象上,过点A作y轴的垂线交反比例函数的图象于点B,交y轴于点M,点P在x轴上,连接 , 求的面积;(2)、直线交反比例函数的图象于点C,交反比例函数的图象于点D,若 , 求n的值.21. 每年的12月4日是我国的“宪法宣传日”,某中学都会在这一天举行宪法知识竞赛,并随机抽取了部分学生的竞赛成绩(优秀:85~100分;良好:70~84分;合格:60~69分;不合格:59分以下)进行调查,将所得数据进行分类,统计绘制了如下不完整的统计图.请根据图中的信息,解答下列问题: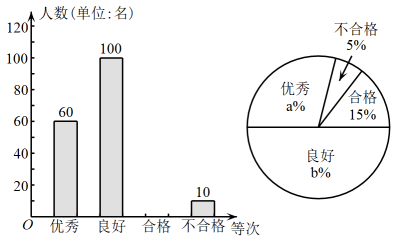 (1)、本次调查的学生共名;a=;b=;并补全条形统计图;(2)、本次调查的学生宪法知识竞赛成绩的中位数在哪个等次(直接写出结果);(3)、若该校共有2800名学生,请估计该校这次宪法知识竞赛成绩在良好及以上等次的人数.
(1)、本次调查的学生共名;a=;b=;并补全条形统计图;(2)、本次调查的学生宪法知识竞赛成绩的中位数在哪个等次(直接写出结果);(3)、若该校共有2800名学生,请估计该校这次宪法知识竞赛成绩在良好及以上等次的人数.