安徽省安庆市2023年中考一模数学试卷
试卷更新日期:2023-04-25 类型:中考模拟
一、单选题
-
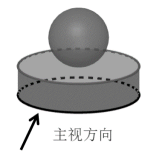
1. 在这四个数中最小的数是( )A、-1 B、1 C、2 D、02. 下列计算中,正确的是( ).A、 B、 C、 D、3. 全球海洋总面积约为36200万平方公里,其中36200万用科学记数法表示为( )A、 B、 C、 D、4. 如图所示几何体是由一个球体和一个圆柱组成的,它的左视图是( )
 A、
A、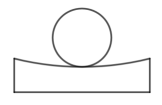 B、
B、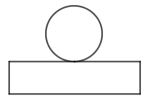 C、
C、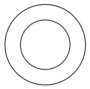 D、
D、 5. 一杆古秤在称物时的状态如图所示,已知 , 则的度数为( )
5. 一杆古秤在称物时的状态如图所示,已知 , 则的度数为( ) A、 B、 C、 D、6. 下列分解因式正确的是( )A、 B、 C、 D、7. 现代电子技术飞速发展,许多家庭都用起了密码锁,只要符合题意输入密码即可打开门.小明家的密码锁密码由六个数字组成,每个数字都是从中任选的,小明记得前五个数字,第六个数字只记得是偶数,他一次随机试验就能打开门的概率为( )A、 B、 C、 D、8. 一次函数的与的部分对应值如下表所示:
A、 B、 C、 D、6. 下列分解因式正确的是( )A、 B、 C、 D、7. 现代电子技术飞速发展,许多家庭都用起了密码锁,只要符合题意输入密码即可打开门.小明家的密码锁密码由六个数字组成,每个数字都是从中任选的,小明记得前五个数字,第六个数字只记得是偶数,他一次随机试验就能打开门的概率为( )A、 B、 C、 D、8. 一次函数的与的部分对应值如下表所示:x
…
-2
1
3
…
y
…
7
4
2
…
根据表中数据分析,下列结论正确的是( ).
A、该函数的图象与轴的交点坐标是(4,0) B、该函数的图象经过第一、二、四象限 C、若点(2,)、(4,)均在该函数图象上,则 D、将该函数的图象向上平移5个单位长度得的图象9. 已知三个实数a,b,c满足 , 则下列结论正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 如图,点是反比例函数图象第二象限上的两点,射线交轴于点 , 且恰好为中点,过点作轴的平行线,交射线于点 , 若的面积为 , 则的值为( )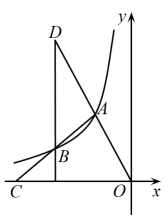 A、-6 B、-4 C、-8 D、-10
A、-6 B、-4 C、-8 D、-10二、填空题
-
11. 计算: .12. 若关于x的方程有两个相等的实数根,则k的值为.13. 如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD= .
 14. 如图,在三角形纸片ABC中, , , 垂直平分 , 平分 , 将沿在上,在上)折叠,点C与点O恰好重合,
14. 如图,在三角形纸片ABC中, , , 垂直平分 , 平分 , 将沿在上,在上)折叠,点C与点O恰好重合, (1)、 ;(2)、若 , 则 .
(1)、 ;(2)、若 , 则 .三、解答题
-
15. 解不等式:16. 在正方形网格中,每个小正方形的边长为1,在平面直角坐标系中的位置如图所示.
 (1)、作出关于轴的对称图形;(2)、作出绕点逆时针旋转后的图形;17. 观察下列式子:
(1)、作出关于轴的对称图形;(2)、作出绕点逆时针旋转后的图形;17. 观察下列式子:···
根据上述规律,回答下列问题:
(1)、请把第4个式子补充完整:;(2)、通过以上算式,我们发现若用来表示个位数字是5的两位数,它的平方有一定的规律,请写出猜想并证明.18. 我国航天事业的飞速发展引发了航空航天纪念品的热销,某商店准备购进甲、乙两类关于航空航天的纪念品进行销售.已知甲类纪念品的进价为m元/件,乙类纪念品的进价比甲类的进价多5元/件.若每件甲类纪念品的售价是在其进价的基础上提高了 , 每件乙类纪念品的售价是在其进价的基础上提高了 , 根据上述条件,回答下面问题:(1)、请用含有m的代数式填写下表:进价/元
售价/元
甲类纪念品
m
乙类纪念品
(2)、该商店分别购进甲类纪念品100件,乙类纪念品80件.两类纪念品全部售出后所得的总利润为1080元,问每件甲、乙两类纪念品进价分别多少元?19. 备受瞩目的卡塔尔世界杯掀起了全民足球运动的热潮.下图为某中学的矩形足球场的一部分,点A、B为球门边框(不考虑球门的高度)的两个端点,米,于点D.某学生沿向球门进攻,在Q点起脚射门,此时射门角 , . 求射门点Q到球门的距离的长度.(结果保留整数)(参考数据:) 20. 如图,在中,以的边为直径作 , 交于点D,是的切线,且 , 垂足为点E.
20. 如图,在中,以的边为直径作 , 交于点D,是的切线,且 , 垂足为点E. (1)、求证:;(2)、若 , 求直径长.21. 为了庆祝党的二十大的顺利召开,也为了让学生更好地铭记历史,某学校在八年级举行党史知识测试,并将测试成绩分为以下4组(x表示成绩,满分100分):
(1)、求证:;(2)、若 , 求直径长.21. 为了庆祝党的二十大的顺利召开,也为了让学生更好地铭记历史,某学校在八年级举行党史知识测试,并将测试成绩分为以下4组(x表示成绩,满分100分):现随机抽取n位同学的成绩进行统计,制成如下统计图表,部分信息如下:
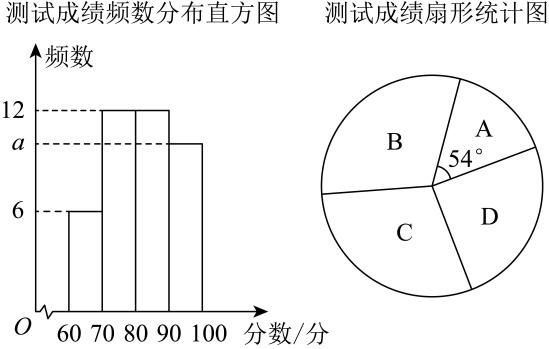
请根据以上信息,完成下列各题:
(1)、n=;a=(2)、样本中成绩的中位数在组.(3)、若成绩不低于90分,则视为优秀等级.已知抽取的样本容量占八年级总学生数的5%,请估计八年级在此次知识测试中大约有多少名学生获优秀等级?22. 某公司生产的一种季节性产品,其单件成本与售价随季节的变化而变化.据调查:
①该种产品一月份的单件成本为6.6元/件,且单件成本每月递增0.2元/件;
②该种产品一月份的单件售价为5元/件,六月份的单件售价最高可达到10元/件,单件售价y(元/件)与时间x(月)的二次函数图象如图所示.
(1)、求该产品在六月份的单件生产成本;(2)、该公司在哪个月生产并销售该产品获得的单件收益w最大?(3)、结合图象,求在全年生产与销售中一共有几个月产品的单件收益不亏损?(注:单件收益=单件售价-单件成本)23. 如图1,在中, , , , 点D在边上(不与点B重合),以为一边作正方形 , 连接 . (1)、如图2,当时,
(1)、如图2,当时,① 求正方形的边长;
② 求证:;
(2)、当点D在上运动时,求面积的最大值.