江西省赣州市南康区2022-2023学年七年级下学期数学期中联考试卷

试卷更新日期：2023-04-25 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标，其中，可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 在 $- \frac{11}{3}$ 、 $\sqrt[3]{9}$ 、 $0.444$ 、 $3.1415926$ 、 $\sqrt{7}$ 、 $0.1$ 、 $2$ 这七个数中，无理数的个数为（）

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
3. 在平面直角坐标系中，若点 $A (m ， - n)$ 在第一象限内，则点 $B (n ， m)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，点E在 $B C$ 的延长线上，下列条件中不能判定 $A B ∥ C D$ 的是（）

A、 $∠ B = ∠ D C E$ B、 $∠ B + ∠ B C D = 180 °$ C、 $∠ 3 = ∠ 4$ D、 $∠ 1 = ∠ 2$

查看试题解析
5. 如图，如果AB∥EF，EF∥CD，下列各式正确的是（）

A、∠1+∠2−∠3=90° B、∠1−∠2+∠3=90° C、∠1+∠2+∠3=90° D、∠2+∠3−∠1=180°

查看试题解析
6. 如图，一个粒子在第一象限内及x轴、y轴上运动，在第一分钟，它从原点运动到点（1，0），第二分钟，它从点（1，0）运动到点（1，1），而后它接着按图中箭头所示在与x轴，y轴平行的方向上来回运动，且每分钟移动1个单位长度，那么在第2022分钟时，这个粒子所在位置的坐标是（　　）

A、（44，5） B、（44，2） C、（45，5） D、（45，2）

查看试题解析

二、填空题

7. 把命题“等角的补角相等”改写成“如果…那么…”的形式是．

查看试题解析
8. 已知点 $A (5 x + 6 ， x - 14)$ 在一、三象限的角平分线上，则x= ．

查看试题解析
9. 如图，将 $R t △ A B C$ 沿着点B到C的方向平移到 $△ D E F$ 的位置， $A B = 10$ ， $D O = 4$ ，平移距离为 $6$ ，则阴影部分面积为．

查看试题解析
10. 已知 $\sqrt{32.56} = 5.706$ ， $\sqrt{325.6} = 18.044$ ，则 $- \sqrt{0.3256} =$ ．

查看试题解析
11. 下面的图表是我国数学家发明的“杨辉三角”，此图揭示了 ${(a + b)}^{n}$ （ $n$ 为非负整数）的展开式的项数及各项系数的有关规律，请你观察，并根据此规律写出： ${(a + b)}^{5} =$ ．

查看试题解析
12. 如图， $∠ A O C = ∠ B O D = 90 °$ ， $∠ A O B = 70 °$ ，在∠AOB内画一条射线OP得到的图中有m对互余的角，其中 $∠ A O P = x °$ ，且满足 $0 < x < 50$ ，则 $m =$ ．

查看试题解析

三、解答题

13. 计算：

(1)、 $\sqrt{4} + | - 2 | + \sqrt[3]{- 64} + {(- 1)}^{2022}$

(2)、 ${(- \sqrt{3})}^{2} + \sqrt{{(- 5)}^{2}} - (- 7) + \sqrt[3]{- 8} \div 2$

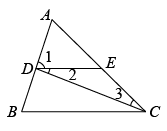
查看试题解析
14. 求下列各式中的x的值：

(1)、 $4 x^{2} = 81$

(2)、 $\frac{1}{3} {(x - 1)}^{3} + 9 = 0$

查看试题解析
15. 已知△ABC中，CD平分∠ACB，∠2=∠3，∠B=70° 求∠1的度数．

查看试题解析
16. 已知a+1的算术平方根是3，-27的立方根是b-12，c-3的平方根是±2.求：

(1)、a，b，c的值；

(2)、a+4b-4c的平方根．

查看试题解析
17. 如图，在7×7正方形网格中的每个小正方形边长都为1个单位长度，我们把每个小正方形的顶点称为格点，点A、B都为格点，请分别仅用一把无刻度的直尺在所给的网格中画图，保留画图过程的痕迹．

(1)、在如图1中找一格点C，画一条线段AB的平行线段CD；

(2)、在图2中找一格点E，画出三角形ABE，使得S_△ABE＝4．

查看试题解析
18. 已知：如图，点E、F分别是AB、CD上的点，DE、AF分别交BC于G、H，∠A＝∠D，∠1＝∠2，
试说明∠B＝∠C．阅读下面的解题过程，在横线上补全推理过程或依据．
解：
∵∠1＝∠2（已知）
∠1＝∠3（           ）
∴∠2＝∠3（等量代换）
∴_▲_（           ）
∴∠4＝_▲_（           ）
又∵∠A＝∠D（已知）
∴∠4＝∠A（等量代换）
∴_▲_（           ）
∴∠B＝∠C（           ）

查看试题解析
19. 已知点 $A (- 2 ， 0)$ ， $B (0 ， 4)$ ， $C (m + 1 ， 2 - m)$ ．

(1)、当点C在y轴上时，求 $△ A B C$ 的面积；

(2)、当 $B C ∥ x$ 轴时，求B、C点之间的距离；

(3)、若P是x轴上一点，且满足 $S_{△ A P B} = \frac{1}{2} S_{△ A O B}$ ，求点P的坐标

查看试题解析
20. 大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，但是由于1 $＜ \sqrt{2} ＜$ 2，所以 $\sqrt{2}$ 的整数部分为1，将 $\sqrt{2}$ 减去其整数部分1，差就是小数部分为（ $\sqrt{2} -$ 1）．
解答下列问题：

(1)、 $\sqrt{10}$ 的整数部分是，小数部分是；

(2)、如果 $\sqrt{6}$ 的小数部分为a； $\sqrt{13}$ 的整数部分为b，求a+b $- \sqrt{6}$ 的值；

(3)、已知15 $+ \sqrt{3} =$ x+y，出其中x是整数，且0＜y＜1，求x-y的相反数．

查看试题解析
21. 如图，已知CF是∠ACB的平分线，交AB于点F，D，E，G分别是AC，AB，BC上的点，且∠3＝∠ACB，∠4+∠5＝180°．

(1)、图中∠1与∠3是一对， ∠2与∠5是一对（填“同位角”或“内错角”或“同旁内角”）；

(2)、判断CF与DE是什么位置关系？说明理由；

(3)、若CF⊥AB，垂足为F，∠A＝58°，求∠ACB的度数．

查看试题解析
22. 先阅读下面一段文字，再回答问题：已知在平面直角坐标系xOy中对于任意两点P₁（x₁ ， y₁）与R（x₂ ， y₂）的“识别距离”，给出如下定义：若|x₁-x₂|≥|y₁-y₂|，则点，P₁（x₁ ， y₁）与P₂（x₂ ， y₂）的“识别距离”为|x₁-x₂|；若|x₁-x₂||＜|y₁-y₂|，则点P₁（x₁ ， y1）与P₂（x₂ ， y₂）的“识别距离”为|y₁-y₂|；

(1)、已知点A（-1，0）；B为y轴上的动点．
①若点A与点B的“识别距离”为3，写出满足条件的点B的坐标．
②直接写出点A与点B的“识别距离”的最小值为．

(2)、已知点C（m， $\frac{3}{4}$ m+3）；D（1，1），求点C与点D的“识别距离”的最小值及相应的点C的坐标．

查看试题解析
23. 如图，在以点O为原点的平面直角坐标系中点A ， B的坐标分别为（a ， 0），（a ， b），点C在y轴上，且BC $//$ x轴，a ， b满足 $| a - 3 | + \sqrt{b - 4} = 0$ ．点P从原点出发，以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动（回到O为止）．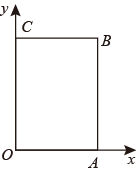

(1)、直接写出点A ， B ， C的坐标；

(2)、当点P运动3秒时，连接PC ， PO ，求出点P的坐标，并直接写出∠CPO ， ∠BCP ， ∠AOP之间满足的数量关系；

(3)、点P运动t秒后（t≠0），是否存在点P到x轴的距离为 $\frac{1}{2}$ t个单位长度的情况．若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析