安徽省安庆市2022-2023学年七年级下学期期中综合素质调研考试数学试题
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 下列各式中没有算术平方根的是( )A、 B、0 C、 D、2. 面积是3的正方形的边长是( )A、整数 B、无理数 C、有理数 D、分数3. 下列各组数中,互为相反数的一组是( )A、与 B、与 C、与 D、与4. 若 , 则下列等式成立的是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、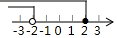 C、
C、 D、
D、 6. 下列运算中,正确的是( )A、 B、 C、 D、7. 是指大气中直径小于或等于的颗粒物,将用科学记数法可表示为( )A、 B、 C、 D、8. 如果不等式组的解集是x<3,那么m的取值范围是( )A、m< B、m≥ C、m<3 D、m≥39. 我国宋朝数学家杨辉在他的著作《详解九章》算法中提出“杨辉三角”如图,此图揭示了(n为非负整数)展开式的项数及各项系数的有关规律.
6. 下列运算中,正确的是( )A、 B、 C、 D、7. 是指大气中直径小于或等于的颗粒物,将用科学记数法可表示为( )A、 B、 C、 D、8. 如果不等式组的解集是x<3,那么m的取值范围是( )A、m< B、m≥ C、m<3 D、m≥39. 我国宋朝数学家杨辉在他的著作《详解九章》算法中提出“杨辉三角”如图,此图揭示了(n为非负整数)展开式的项数及各项系数的有关规律.
例如:
…
请你猜想的展开式中所有系数的和是( )
A、 B、 C、 D、10. 已知 , 则代数式的值是( )A、2 B、1 C、3 D、二、填空题
-
11. 如果 ,那么 等于 .12. 不等式x-1≤的解集是 .13. 已知 , 则的值为 .14. 任意一个无理数介于两个整数之间,我们定义:若无理数T:m<T<n(其中m为满足不等式的最大整数,n为满足不等式的最小整数),则称无理数T的“雅区间”为(m,n).例如:1<<2,所以的“雅区间”为(1,2).(1)、无理数的“雅区间”是;(2)、若某一无理数的“雅区间”为(m,n),且满足0<<12,其中是关于x,y的二元一次方程mx-ny=c的一组正整数解,则c的值为 .
三、解答题
-
15. 计算: .16. 解不等式组 ,并把解集在数轴上表示出来.17. 为把A市建成秀美、宜居的生态城市,市政府欲购买甲、乙、丙三种风景树美化环境.已知甲、乙、丙三种风景树的价格之比为 , 甲种风景树每棵元.若计划用元资金,购买这三种风景树共棵,求丙种风景树最多可以购买多少棵?18. 已知 , , 求:(1)、的值;(2)、的值.19.(1)、试证明代数式的值与x的值无关,(2)、若的展开式中不含和的项,求m,n的值.20. 已知:关于、的方程组:(1)、求这个方程组的解:(用含有字母的代数式表示)(2)、若这个方程组的解满足为非负数,为负数,求字母的取值范围21. 先观察下列等式,再回答问题
①;
②;
③ .
(1)、请你根据上面三个等式提供的信息,猜想==;== .(2)、请你按照上面各等式反映的规律,试写出用含n的式子表示的等式(n为正整数).22. 用“◇”和“☆”分别代表甲种植物和乙种植物,为了美化环境,采用如图所示的方案种植. (1)、观察图形,寻找规律,并填写下表:
(1)、观察图形,寻找规律,并填写下表:图序
①
②
③
④
⑤
⑥
◇
☆
(2)、求出第n个图形中甲种植物和乙种植物的株数;(3)、是否存在一种种植方案,使得乙种植物的株数是甲种植物的株数的2倍?若存在,请你写出是第几个方案,若不存在,请说明理由.23. 如图1,有A型、B型、C型三种不同形状的纸板,A型是边长为a的正方形,B型是边长为b的正方形,C型是长为b,宽为a的长方形.现用A型纸板一张,B型纸板一张,C型纸板两张拼成如图2的大正方形. (1)、观察图2,请你用两种方法表示出图2的总面积.
(1)、观察图2,请你用两种方法表示出图2的总面积.方法1:;
方法2:;
请利用图2的面积表示方法,写出一个关于a,b的等式: .
(2)、已知图2的总面积为 , 一张A型纸板和一张B型纸板的面积之和为 , 求的值.(3)、用一张A型纸板和一张B型纸板,拼成图3所示的图形,若 , , 求图3中阴影部分的面积.