山西省晋中市介休市2022-2023学年八年级下学期期中质量评估数学试题
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 满足 的最大整数 是( )A、1 B、2 C、3 D、42. 如图,下列四组图形中,每两个“F”之间属于平移变换的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若 , 则下列各式错误的是( )A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、
3. 若 , 则下列各式错误的是( )A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、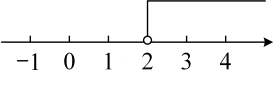 D、
D、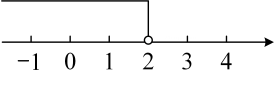 5. 下列四个图分别是我国四家航空公司的logo,其中属于中心对称图形的是( )A、南方航空
5. 下列四个图分别是我国四家航空公司的logo,其中属于中心对称图形的是( )A、南方航空 B、东海航空
B、东海航空 C、重庆航空
C、重庆航空 D、海南航空
D、海南航空 6. 小颖同学根据“一次函数的图象与x轴的交点”,判断关于x的一元一次不等式的解集为 , 小颖同学在解决这个问题时用到的数学思想是( )A、数形结合思想 B、分类讨论思想 C、公理化思想 D、模型思想7. 如图①是两位同学玩跷跷板的场景,如图②跷跷板示意图,支柱与地面垂直,点O是的中点,绕着点O上下转动.若A端落地时, , 则跷跷板上下可转动的最大角度(即)是( )
6. 小颖同学根据“一次函数的图象与x轴的交点”,判断关于x的一元一次不等式的解集为 , 小颖同学在解决这个问题时用到的数学思想是( )A、数形结合思想 B、分类讨论思想 C、公理化思想 D、模型思想7. 如图①是两位同学玩跷跷板的场景,如图②跷跷板示意图,支柱与地面垂直,点O是的中点,绕着点O上下转动.若A端落地时, , 则跷跷板上下可转动的最大角度(即)是( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )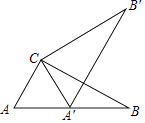 A、12 B、6 C、6 D、9. 如图,一次函数 的图像经过 , 两点,则 解集是( )
A、12 B、6 C、6 D、9. 如图,一次函数 的图像经过 , 两点,则 解集是( ) A、 B、 C、 D、10. 如图,在中, , , 为的中点,于点N,则的长度为( )
A、 B、 C、 D、10. 如图,在中, , , 为的中点,于点N,则的长度为( )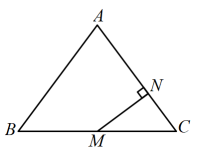 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
11. 如图,左边物体的质量为xg,右边物体的质量为50g,用不等式表示下列数量关系是 .
 12. 如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为 .
12. 如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为 . 13. 如图所示的图案由形状相同的三个叶片组成,绕点O旋转后可以和自身重合.若每个叶片的面积为 , 为 , 则图中阴影部分的面积之和为 .
13. 如图所示的图案由形状相同的三个叶片组成,绕点O旋转后可以和自身重合.若每个叶片的面积为 , 为 , 则图中阴影部分的面积之和为 .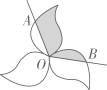 14. 台灯的光亮照射范围相对比较集中,便于阅读、学习、工作且节省能源.某款稻草人小台灯进价10元,标价15元,商店为了促销,决定打折销售,但每台利润不少于2元,则最多可打折销售.
14. 台灯的光亮照射范围相对比较集中,便于阅读、学习、工作且节省能源.某款稻草人小台灯进价10元,标价15元,商店为了促销,决定打折销售,但每台利润不少于2元,则最多可打折销售. 15. 如图,在△ABC中,AB=10,AC=8,∠BAC=45°,AD是∠BAC的平分线, DE⊥AB于点E,则DE的长是
15. 如图,在△ABC中,AB=10,AC=8,∠BAC=45°,AD是∠BAC的平分线, DE⊥AB于点E,则DE的长是
三、解答题
-
16. 下面是小颖同学解一元一次不等式的解答过程,请认真阅读并完成相应任务.
解:去分母,得 , ………………………………第一步去括号,得……………………………………………第二步
移项、合并同类项,得 , …………………………………………第三步
两边都除以3,得 . ………………………………………………第四步
任务一:填空:
①以上运算步骤中,去分母的依据是;
②第二步变形所依据的运算律是;
③第步开始出现错误,这一步错误的原因是;
任务二:请直接写出正确的计算结果 .17. 解下列不等式组,并在数轴上表示出不等式组的解集:(1)、(2)、18. 如图,在 中, , . (1)、通过观察尺规作图的痕迹,可以发现直线 是线段 的 , 射线 是 的;(2)、在(1)所作的图中,求 的度数.19. 列不等式解应用题:
(1)、通过观察尺规作图的痕迹,可以发现直线 是线段 的 , 射线 是 的;(2)、在(1)所作的图中,求 的度数.19. 列不等式解应用题:为提高超市的食品销售价格,超市老板抓住商机,从厂家购进了A,B两种型号食品,其数量和进价如表:
型 号
数 量(箱)
进价(元/箱)
A
10
48元
B
5
122元
为使每箱B型号食品售价是每箱A型号食品售价的2倍,且保证售完这批食品的利润不低于170元,每箱A型食品的售价至少应为多少元?(注:利润=售价-进价).
20. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,坐标分别为A(2,2),B(1,0),C(3,1).
( 1 )画出△ABC关于y轴对称的△;
( 2 )画出将△ABC绕原点O顺时针旋转90°所得的△;
( 3 )△与△2成中心对称图形吗?若成中心对称图形,直接写出对称中心的坐标.
21. 阅读下面的“数学活动报告”,并完成相应学习任务.作的平分线活动内容:
已知 , 作出的平分线 .
方法展示:
方案一:如图①,分别在的边 , 上截取 , 再分别以点M,N为圆心,大于长为半径画弧,两弧相交于点C,则射线就是的平分线.
方案二:如图②,分别在的边 , 上用圆规截取 , 再利用三角尺分别过点 , 作出 , 的垂线,两条垂线交于点C,作射线 , 则就是的平分线.
方案三:如图③,在上取一点P,过点P作;然后在上截取 , 作射线 , 就是的平分线.
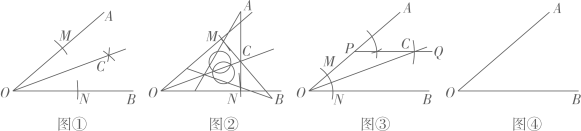
活动总结:
全等三角形、等腰三角形的性质是证明两角相等的重要依据,根据全等三角形、等腰三角形的有关知识可以用多种方法作的平分线.
活动反思:
利用等腰三角形“三线合一”的性质可以作出的平分线吗?
学习任务:
(1)、方案一依据的一个基本事实是;方案二“判定直角三角形全等”的依据是;(2)、同学们提出的方案三是否符合题意?请你利用图③说明理由;(3)、请依据等腰三角形“三线合一”的性质,在图④中作出的平分线,并简要叙述作图过程.22. “人说山西好风光,地肥水美五谷香”.山西复杂的地形、多样的气候、丰富的杂粮品种资源,成就了山西“小杂粮王国”的美誉,某杂粮经销商对本地购买20袋以上杂粮的客户有两种销售方案(客户只能选择其中一种方案):方案一:每袋30元,由经销商免费送货;
方案二:每袋26元,客户需支付运费200元.
某粮油公司计划购买袋该经销商的杂粮,请解答下列问题:
(1)、按方案一购买该杂粮应付的费用为 , 按方案二购买该杂粮应付的费用为;(2)、当购买量在什么范围时,方案一比方案二更省钱?(3)、某粮油公司计划拿出30000元用于采购该经销商的杂粮,选择方案(填“一”或“二”)能买到更多的杂粮.23. 综合与实践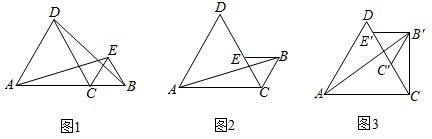
问题情境
数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动,△ACD和△BCE是两个等边三角形纸片,其中,AC=5cm,BC=2cm.
解决问题
(1)、勤奋小组将△ACD和△BCE按图1所示的方式摆放(点A,C,B在同一条直线上),连接AE,BD.发现AE=DB,请你给予证明;(2)、如图2,创新小组在勤奋小组的基础上继续探究,将△BCE绕着点C逆时针方向旋转,当点E恰好落在CD边上时,求△ABC的面积;拓展延伸
(3)、如图3,缜密小组在创新小组的基础上,提出一个问题:将△BCE沿CD方向平移acm,得到B'C'E',连接AB',B'C,当△AB'C恰好是以AB'为斜边的直角三角形时,求a的值.请你直接写出a的值.