江西省南昌市2022-2023学年八年级下学期期中检测数学试题
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 若式子在实数范围内有意义,则x的取值范围是( )A、x>2 B、x<2 C、x≥2 D、x≤22. 下列运算正确的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点到原点的距离是( )A、1 B、3 C、 D、4. 以下列各数为边长,能构成直角三角形的是( )A、1,2,2 B、1, ,2 C、4,5,6 D、1,1,5. 在平行四边形中,对角线 , 相交于点O, , , 则边的长度x的取值范围是( )A、 B、 C、 D、6. 下列命题中,为真命题的是( )
(1)对角线互相平分的四边形是平行四边形
(2)对角线互相垂直的四边形是菱形
(3)对角线相等的平行四边形是菱形
(4)有一个角是直角的平行四边形是矩形A、(1)(2) B、(1)(4) C、(2)(4) D、(3)(4)二、填空题
-
7. 化简: .8. 一个三角形的三边长分别为 ,则它的周长是cm.9. 直角三角形有两条边长分别为 6 和 8,则第三条边的平方为 .10. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .11. 如图,在 中, ,且 , ,点 是斜边 上的一个动点,过点 分别作 于点 , 于点 ,连接 ,则线段 的最小值为 .
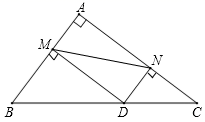 12. 如图,在等腰直角三角形中, , , 点P是边上任意一点,连接 , 将沿翻折,点B的对应点为 , 当有一边与垂直时,的长为 .
12. 如图,在等腰直角三角形中, , , 点P是边上任意一点,连接 , 将沿翻折,点B的对应点为 , 当有一边与垂直时,的长为 .
三、解答题
-
13. 计算:(1)、(2)、14. 已知 , , 求下列各式的值.(1)、和;(2)、 .15. 在中,已知 , , , 试判断的形状,并说明理由.16. 在正方形网格中,四边形ABCD的每个顶点都在格点上,已知小正方形的边长为1,求这个四边形ABCD的周长和面积.
 17. 如图,四边形是菱形,请仅用无刻度的直尺作图(保留作图痕迹,不写做法).
17. 如图,四边形是菱形,请仅用无刻度的直尺作图(保留作图痕迹,不写做法). (1)、在图1中,E,F分别是 , 上的点且 , 以为边作一个矩形;(2)、在图2中,E是对角线上一点,以为边作一个菱形.18. 乐乐从一副七巧板(如图1)中取出了其中的六块,拼成了一个(如图2),已知原来七巧板拼成正方形的边长为4;
(1)、在图1中,E,F分别是 , 上的点且 , 以为边作一个矩形;(2)、在图2中,E是对角线上一点,以为边作一个菱形.18. 乐乐从一副七巧板(如图1)中取出了其中的六块,拼成了一个(如图2),已知原来七巧板拼成正方形的边长为4; (1)、图2中小正方形②的边长=;线段;(2)、求对角线的长.19. 已知a,b,m都是实数,若 , 则称a与b是关于l的“平衡数”.(1)、-1与是关于l的“平衡数”,与是关于l的“平衡数”;(2)、若 , 判断与是否是关于l的“平衡数”,并说明理由.20. 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)、图2中小正方形②的边长=;线段;(2)、求对角线的长.19. 已知a,b,m都是实数,若 , 则称a与b是关于l的“平衡数”.(1)、-1与是关于l的“平衡数”,与是关于l的“平衡数”;(2)、若 , 判断与是否是关于l的“平衡数”,并说明理由.20. 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形). (1)、四边形EFGH的形状是 .(2)、证明你的结论.(3)、当满足时,四边形是菱形.(4)、当满足时,四边形是矩形.(5)、当满足时,四边形是正方形.21. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,与地面垂直,两脚在地面上用力一蹬,妈妈在距地面的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到的水平距离 , 分别为和 , , 于点D,于点E,
(1)、四边形EFGH的形状是 .(2)、证明你的结论.(3)、当满足时,四边形是菱形.(4)、当满足时,四边形是矩形.(5)、当满足时,四边形是正方形.21. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,与地面垂直,两脚在地面上用力一蹬,妈妈在距地面的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到的水平距离 , 分别为和 , , 于点D,于点E, (1)、求证:;(2)、求秋千的起始位置A距地面的高AM.22. 如图,在四边形中, , , , , , 点P从点A出发,以的速度向点D运动;点Q从点C同时出发,以的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P的运动时间为t;
(1)、求证:;(2)、求秋千的起始位置A距地面的高AM.22. 如图,在四边形中, , , , , , 点P从点A出发,以的速度向点D运动;点Q从点C同时出发,以的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P的运动时间为t; (1)、边的长度为 , t的最大值为;(2)、当t为何值时,四边形是矩形;(3)、当时,判断此时四边形的形状,并说明理由;23. 【课本再现】如图,四边形是正方形,点E是边的中点, , 且交正方形外角的平分线于点F.
(1)、边的长度为 , t的最大值为;(2)、当t为何值时,四边形是矩形;(3)、当时,判断此时四边形的形状,并说明理由;23. 【课本再现】如图,四边形是正方形,点E是边的中点, , 且交正方形外角的平分线于点F.
 (1)、求证.(提示:取的中点G,连接);(2)、【类比迁移】如图2,若点E是边上任意一点(不与B,C重合),其他条件不变,求证:;(3)、【拓展应用】在(2)的条件下,连接 , 过点E作于P,当时,如图3,请判断四边形的形状,并说明理由.
(1)、求证.(提示:取的中点G,连接);(2)、【类比迁移】如图2,若点E是边上任意一点(不与B,C重合),其他条件不变,求证:;(3)、【拓展应用】在(2)的条件下,连接 , 过点E作于P,当时,如图3,请判断四边形的形状,并说明理由.