广东省中山市小榄镇2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 若二次根式 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列各组数是三角形的三边,不能组成直角三角形的一组数是( )A、3,4,5 B、6,8,10 C、1,1, D、 , ,3. 下列计算正确的是( )A、 B、 C、 D、4. 下列命题中,假命题是( )A、对角线垂直的平行四边形是菱形 B、对角线互相平分且垂直的四边形是菱形 C、对角线互相平分且平分一组内角的四边形是菱形 D、对角线相等且垂直的四边形是菱形5. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、6. 如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
 A、AB=CD,AD=BC B、AB∥CD,AD∥BC C、AB∥CD,AD=BC D、AD∥BC,AD=BC7. 若顺次连接四边形各边中点所得的四边形是菱形,则该四边形一定是( )A、矩形 B、一组对边相等,另一组对边平行的四边形 C、对角线相等的四边形 D、对角线互相垂直的四边形8. 如图,数轴上的点A表示的数是-1,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
A、AB=CD,AD=BC B、AB∥CD,AD∥BC C、AB∥CD,AD=BC D、AD∥BC,AD=BC7. 若顺次连接四边形各边中点所得的四边形是菱形,则该四边形一定是( )A、矩形 B、一组对边相等,另一组对边平行的四边形 C、对角线相等的四边形 D、对角线互相垂直的四边形8. 如图,数轴上的点A表示的数是-1,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )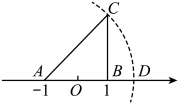 A、2-1 B、2 C、2.8 D、2+19. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A、2-1 B、2 C、2.8 D、2+19. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( ) A、( ,1) B、(2,1) C、(1, ) D、(2, )10. 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
A、( ,1) B、(2,1) C、(1, ) D、(2, )10. 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF .
其中,将正确结论的序号全部选对的是( )
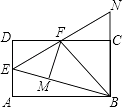 A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
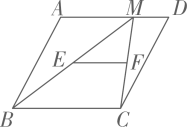
11. 计算 的值为.12. 已知是整数,则正整数n的最小值为 .13. 在平行四边形中,周长为10, , .14. 如图,在平行四边形 中,点M为边 上一点, ,点E,点 分别是 中点,若 ,则 的长为.
 15. 如图,菱形ABCD中,对角线 , , M,N分别是BC,CD上的动点,P是线段BD上的一个动点,则的最小值是 .
15. 如图,菱形ABCD中,对角线 , , M,N分别是BC,CD上的动点,P是线段BD上的一个动点,则的最小值是 .
三、解答题
-
16. 计算: .17. 如图,在Rt ABC中,∠ACB=90°,CD是斜边AB上的中线,AC=4,CD=3.求直角边BC的长.
 18. 已知:如图,在 ABCD中,延长线AB至点E , 延长CD至点F , 使得BE=DF . 连接EF , 与对角线AC交于点O . 求证:OE=OF .
18. 已知:如图,在 ABCD中,延长线AB至点E , 延长CD至点F , 使得BE=DF . 连接EF , 与对角线AC交于点O . 求证:OE=OF .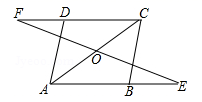 19. 已知 , , 求下列代数式的值:(1)、;(2)、 .20. 如图,在▱ABCD中,点E在BC的延长线上,且CE=BC , AE=AB , AE、DC相交于点O , 连接DE .
19. 已知 , , 求下列代数式的值:(1)、;(2)、 .20. 如图,在▱ABCD中,点E在BC的延长线上,且CE=BC , AE=AB , AE、DC相交于点O , 连接DE .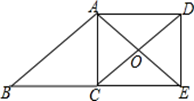 (1)、求证:四边形ACED是矩形;(2)、若∠AOD=120°,AC=4,求对角线CD的长.21. 如图,小区有一块三角形空地 , 为响应中山市创建全国文明典范城市的号召,小区计划将这块空地种上三种不同的花卉,中间用小路隔开, . 经测量,米,米,米,米.
(1)、求证:四边形ACED是矩形;(2)、若∠AOD=120°,AC=4,求对角线CD的长.21. 如图,小区有一块三角形空地 , 为响应中山市创建全国文明典范城市的号召,小区计划将这块空地种上三种不同的花卉,中间用小路隔开, . 经测量,米,米,米,米. (1)、求的长;(2)、求小路的长22. 如图,在矩形中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接、、 . 设点P、Q运动的时间为ts.
(1)、求的长;(2)、求小路的长22. 如图,在矩形中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接、、 . 设点P、Q运动的时间为ts. (1)、当t为何值时,四边形是矩形;(2)、当t为何值时,四边形是菱形;(3)、分别求出(2)中菱形的周长和面积.23. 如图,在中, , 过点C的直线 , D为边上一点,过点D作 , 交直线于E,垂足为F,连接、 .
(1)、当t为何值时,四边形是矩形;(2)、当t为何值时,四边形是菱形;(3)、分别求出(2)中菱形的周长和面积.23. 如图,在中, , 过点C的直线 , D为边上一点,过点D作 , 交直线于E,垂足为F,连接、 .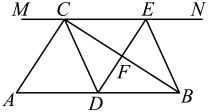 (1)、求证:;(2)、当D在中点时,四边形是什么特殊四边形?请说明你的理由;(3)、若D为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.
(1)、求证:;(2)、当D在中点时,四边形是什么特殊四边形?请说明你的理由;(3)、若D为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.