安徽省宿州市泗县2022—2023学年八年级下学期期中考试数学试卷
试卷更新日期:2023-04-25 类型:期中考试
一、单选题
-
1. 下列汽车标识中既是轴对称图形,又是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 已知点在第二象限,则a的取值范围在数轴上表示正确的是( )A、
2. 已知点在第二象限,则a的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,是的边的垂直平分线,为垂足,交于点 , 且 , , , 则的周长是( )
3. 如图,是的边的垂直平分线,为垂足,交于点 , 且 , , , 则的周长是( )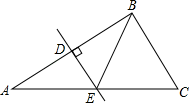 A、14 B、16 C、18 D、224. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 如图,把绕着点C顺时针方向旋转 , 得到 , 点B刚好落在边上,则的度数为( )
A、14 B、16 C、18 D、224. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 如图,把绕着点C顺时针方向旋转 , 得到 , 点B刚好落在边上,则的度数为( ) A、 B、 C、 D、6. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 若多项式能分解成两个一次因式的积,且其中一个次因式 , 则a的值为( )A、1 B、5 C、 D、8. 一次函数与的图象如图所示,则的解集为( )
A、 B、 C、 D、6. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 若多项式能分解成两个一次因式的积,且其中一个次因式 , 则a的值为( )A、1 B、5 C、 D、8. 一次函数与的图象如图所示,则的解集为( )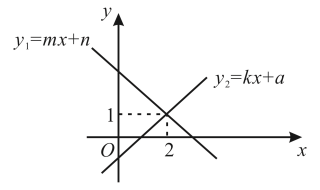 A、 B、 C、 D、9. 如图,在中, , , 点D为中点,直角绕点D旋转, , 分别与边 , 交于E,F两点,下列结论:①;②是等腰直角三角形;③;④ , 其中正确结论是( )
A、 B、 C、 D、9. 如图,在中, , , 点D为中点,直角绕点D旋转, , 分别与边 , 交于E,F两点,下列结论:①;②是等腰直角三角形;③;④ , 其中正确结论是( ) A、①②④ B、②③④ C、①②③ D、①②③④10. 如图,边长为6的等边三角形中,E是对称轴上一个动点,连接 , 将线段绕点C逆时针旋转60度得到 , 连接 , 则在点E运的过程中,最小值是( )
A、①②④ B、②③④ C、①②③ D、①②③④10. 如图,边长为6的等边三角形中,E是对称轴上一个动点,连接 , 将线段绕点C逆时针旋转60度得到 , 连接 , 则在点E运的过程中,最小值是( ) A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
11. 已知 , , 则 .12. 如图,沿平移后得到 , 点D是点A的对应点,如果 , , 那么平移的距离是 .
 13. 一元一次不等式组的解集是 , 则m的取值范围是 .14. 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CPOB,交OA于点C,PD⊥OB,垂足为点D,且PC=10,则PD的长为 .
13. 一元一次不等式组的解集是 , 则m的取值范围是 .14. 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CPOB,交OA于点C,PD⊥OB,垂足为点D,且PC=10,则PD的长为 . 15. 如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=°.
15. 如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=°. 16. 如图,现有边长为a的正方形1个,边长为b的正方形3个,边长为a,b(a>b)的长方形4个,把它们拼成一个大长方形,请利用这个拼图中图形的面积关系分解因式:a2+4ab+3b2= .
16. 如图,现有边长为a的正方形1个,边长为b的正方形3个,边长为a,b(a>b)的长方形4个,把它们拼成一个大长方形,请利用这个拼图中图形的面积关系分解因式:a2+4ab+3b2= . 17.
17.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP= 时,△ABC和△PQA全等.
 18. 如图,在中, , 是边上的中线, , 则的面积是 .
18. 如图,在中, , 是边上的中线, , 则的面积是 .
三、解答题
-
19.(1)、因式分解: .(2)、解不等式: .20. 如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点,ABC的顶点都在格点上,建立如图所示的平面直角坐标系,点A,B,C的坐标分别为(1,1),(4,2),(2,3).
 (1)、画出ABC向左平移4个单位,再向上平移1个单位后得到的A1B1C1;(2)、画出ABC关于原点O对称的A2B2C2;(3)、求ABC面积.21. 如图,四边形中, , 是对角线,是等边三角形.线段绕点C顺时针旋转得到线段 , 连接 . 求证: .
(1)、画出ABC向左平移4个单位,再向上平移1个单位后得到的A1B1C1;(2)、画出ABC关于原点O对称的A2B2C2;(3)、求ABC面积.21. 如图,四边形中, , 是对角线,是等边三角形.线段绕点C顺时针旋转得到线段 , 连接 . 求证: .
