安徽省安庆市2022-2023学年八年级下学期期中综合素质调研考试数学试题

试卷更新日期：2023-04-25 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{0.5}$ B、 $\sqrt{15}$ C、 $\sqrt{8}$ D、 $\sqrt{9}$

查看试题解析
2. 用配方法解方程 $x^{2} + 8 x + 9 = 0$ ，变形后的结果正确的是（）

A、 ${(x + 4)}^{2} = - 9$ B、 ${(x + 4)}^{2} = - 7$ C、 ${(x + 4)}^{2} = 25$ D、 ${(x + 4)}^{2} = 7$

查看试题解析
3. 下列二次根式中，与 $\sqrt{6}$ 是同类二次根式的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{12}$ C、 $\sqrt{18}$ D、 $\sqrt{0.6}$

查看试题解析
4. 若关于x的一元二次方程 $(a - 2) x^{2} - 8 x + 6 = 0$ 有实数根，则满足条件的正整数a个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 某工厂计划用两年时间使产值增加到目前的4倍，并且使第二年增长的百分数是第一年增长百分数的2倍，设第一年增长的百分数为x，则可列方程得（　　）

A、（1+x）²＝4 B、x（1+2x+4x）＝4 C、2x（1+x）＝4 D、（1+x）（1+2x）＝4

查看试题解析
6. 代数式 $\sqrt{x} + \sqrt{x - 1} + \sqrt{x - 2}$ 的最小值是（　　）

A、0 B、 $1 + \sqrt{2}$ C、1 D、不存在的

查看试题解析
7. $△ A B C$ 三边长分别为a，b，c．下列条件：① $∠ A = ∠ B - ∠ C$ ；② $a ： b ： c = 5 ： 12 ： 13$ ；③ $∠ A ： ∠ B ： ∠ C =$ $3 ： 4 ： 5$ ；④ $a = 3^{2}$ ， $b = 4^{2}$ ， $c = 5^{2}$ ．其中能判断 $△ A B C$ 是直角三角形的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 若关于x的一元二次方程 $a x^{2} + b x + c = 0$ 两根为-2和3，则关于x的方程 $a {(x^{2} - 1)}^{2} + b (x^{2} - 1) + c = 0$ 的实数根个数为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载。如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（）

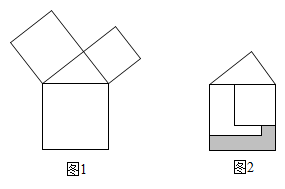A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

查看试题解析
10. 若 $x_{0}$ 是方程 $a x^{2} + 2 x + c = 0 (a \neq 0)$ 的一个根，设 $M = 1 - a c,$ $N = {(a x_{0} + 1)}^{2},$ 则M与N的大小关系正确的为（）

A、 $M > N$ B、 $M = N$ C、 $M < N$ D、不确定

查看试题解析

二、填空题

11. 计算： $\sqrt{{(- 3)}^{2}}$ = ．

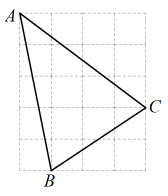
查看试题解析
12. 已知关于x的一元二次方程 $x^{2} + 5 x + 1 - m = 0$ 的一个根是2，则另一个根是．

查看试题解析
13. 如图，正方形网格中，每个小正方形的边长为1，则网格上的三角形 $△ A B C$ 中， $B C$ 边上的高是．

查看试题解析
14. 如图，在锐角 $△ A B C$ 中， $A B = 8$ ， $∠ B A C = 45 °$ ， $∠ B A C$ 的平分线AD交BC于点D，点M，N分别是线段AD和AB上的两个动点，则 $B M + M N$ 的最小值是．

查看试题解析

三、解答题

15. 计算： $\sqrt{3^{3}} + {(- 3 \sqrt{2})}^{2} - \sqrt{48} - 3 \sqrt{\frac{1}{3}}$

查看试题解析
16. 解方程： $2 (x - 3)^{2} = x^{2} - 9$

查看试题解析
17. 已知方程 $x^{2} + (1 - \sqrt{2}) x - \sqrt{2} = 0$ 的两根为 $x_{1} ， x_{2}$ ，求 ${x_{1}}^{2} + {x_{2}}^{2}$ 的值．

查看试题解析
18. 如图，在边长为1个单位长度的小正方形组成的网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画图．

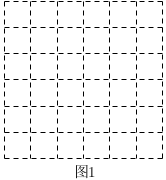
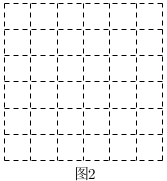(1)、在图1中，画一个正方形，使它的面积为10；

(2)、在图2中，画一个三角形 $A B C$ ，使它的三边长分别为 $A B = \sqrt{5}$ ， $B C = 2 \sqrt{5}$ ， $A C = 5$ ；

(3)、请写出图2中所画 $△ A B C$ 的面积为．（直接写出结果）

查看试题解析
19. 观察下列等式：
第1个等式： $\frac{1}{2} - \frac{1}{4} = \frac{1}{4}$ ；第2个等式： $\frac{1}{3} - \frac{1}{9} = \frac{2}{9}$ ；第3个等式 $\frac{1}{4} - \frac{1}{16} = \frac{3}{16}$ ；…
根据以上规律，解决下列问题：

(1)、写出第4个等式：；

(2)、写出你猜想的第n个等式：（用含n的式子表示），并证明．

查看试题解析
20. 如图，直角三角形纸片的两直角边 $A C = 5 c m$ ， $B C = 12 c m$ ．现将直角边 $A C$ 沿 $A D$ 折叠，使它落在斜边 $A B$ 上，点C点E重合．求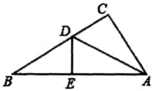 $C D$ 的长．

查看试题解析
21. 阅读材料．
将一个代数式或代数式的某一部分通过改写化为完全平方式或几个完全平方式的和，这种解题方法称为配方法．这种方法常常被用到代数式的恒等变形中，其作用在于揭示代数式的非负性，是挖掘隐含条件的利器，添项，拆项是常用的方法与技巧．
例如，我们可以通过配方法，求代数式 $x^{2} + 6 x + 5$ 的最小值，解题过程如下：
解：∵ $x^{2} + 6 x + 5 = x^{2} + 2 \cdot x \cdot 3 + 3^{2} - 3^{2} + 5 = (x + 3)^{2} - 4$ ，
又∵ $(x + 3)^{2} \geq 0$ ， ∴当 $x = - 3$ 时， $x^{2} + 6 x + 5$ 有最小值为 $- 4$ ．
请根据上述方法，解答下列问题：

(1)、 $x^{2} + 4 x - 1 = x^{2} + 2 \cdot x \cdot 2 + 2^{2} - 2^{2} - 1 = (x + a)^{2} + b$ ，则ab的值是

(2)、若代数式 $x^{2} + k x + 7$ 的最小值为2，求k的值．

查看试题解析
22. 如图，利用一面墙（墙长25米），用总长度49米的橱栏（图中实线部分）围成一个矩形围栏ABCD，且中间共留两个1米的小门，设选栏BC长为x米．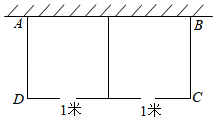

(1)、AB＝　　米（用含x的代数式表示）；

(2)、若矩形围栏ABCD面积为210平方米，求橱栏BC的长；

(3)、矩形围栏ABCD面积是否有可能达到240平方米？若有可能，求出相应x的值；若不可能，则说明理由．

查看试题解析
23. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， D为 $A B$ 中点，点E、F分别在边 $A C 、 B C$ 上，且 $D E ⊥ D F$ ．

(1)、如图1，如果 $C A = C B = 7$ ， $A E = 4$ ，试求 $B F$ 和 $E F$ 的长度；

(2)、猜想线段 $A E 、 B F$ 和 $E F$ 长度之间的数量关系

(3)、如图2，如果 $C A \neq C B$ ，（2）中 $A E 、 B F$ 和 $E F$ 之间的关系还成立吗？若成立，请证明：若不成立，请说明理由．

查看试题解析