山东省淄博市博山区2023年中考一模数学试题
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
1. 在实数 , x0(x≠0),cos30°,中,有理数的个数是( )A、1个 B、2个 C、3个 D、4个2. 下列说法正确的是( )A、命题一定有逆命题 B、所有的定理一定有逆定理 C、真命题的逆命题一定是真命题 D、假命题的逆命题一定是假命题3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,裁掉一个正方形后能折叠成正方体,不能裁掉的是( )
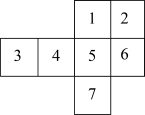 A、1 B、2 C、3 D、65. 某学习小组做摸球试验,在一个不透明的袋子里装有红、黄两种颜色的小球共20个,除颜色外都相同.将球搅匀后,随机摸出5个球,发现3个是红球,估计袋中红球的个数是( )A、12 B、9 C、8 D、66. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、7. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠18. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A、1 B、2 C、3 D、65. 某学习小组做摸球试验,在一个不透明的袋子里装有红、黄两种颜色的小球共20个,除颜色外都相同.将球搅匀后,随机摸出5个球,发现3个是红球,估计袋中红球的个数是( )A、12 B、9 C、8 D、66. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、7. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠18. 几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )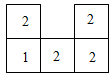 A、3 B、4 C、6 D、99. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
A、3 B、4 C、6 D、99. 如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( ) A、5 B、6 C、 D、10. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( )
A、5 B、6 C、 D、10. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 试卷上一个正确的式子被小颖同学不小心滴上墨汁★.被墨汁★遮住部分的代数式为 .12. 观察如图所示的频数直方图,其中组界为99.5~124.5这一组的频数为 .
 13. 如图,正比例函数与反比例函数的图象交于 , 两点,当时,的取值范围是 .
13. 如图,正比例函数与反比例函数的图象交于 , 两点,当时,的取值范围是 . 14. 关于x,y的方程组的解中x与y的和不小于5,则k的取值范围为 .15. 如图,三角形纸片中, , , . 沿过点A的直线将纸片折叠,使点B落在边上的点D处;再折叠纸片,使点C与点D重合,若折痕与的交点为E,则的长是 .
14. 关于x,y的方程组的解中x与y的和不小于5,则k的取值范围为 .15. 如图,三角形纸片中, , , . 沿过点A的直线将纸片折叠,使点B落在边上的点D处;再折叠纸片,使点C与点D重合,若折痕与的交点为E,则的长是 .
三、解答题
-
16. 先化简,再求值:(a+2b)2+(a+2b)(a-2b)+2a(b-a),其中a=- , b=+ .17. 如图,已知是的一个外角.请用尺规作图法,求作射线 , 使.(保留作图痕迹,不写作法)
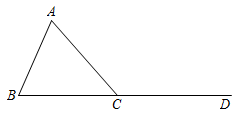 18. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , . 求证:四边形是平行四边形.
18. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , . 求证:四边形是平行四边形.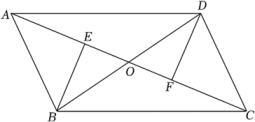 19. 如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高AB=0.75m,斜坡AC的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离ED=2.55m.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度?(结果精确到1)
19. 如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高AB=0.75m,斜坡AC的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离ED=2.55m.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度?(结果精确到1)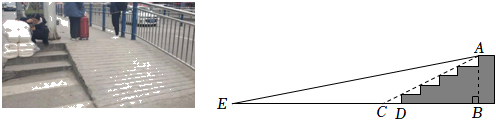
(参考数据表)
计算器按键顺序
计算结果(已精确到0.001)

11.310

0.003
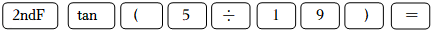
14.744

0.005
20. 中国共产党的助手和后备军——中国共青团,担负着为中国特色社会主义事业培养合格建设者和可靠接班人的根本任务.成立一百周年之际,各中学持续开展了A:青年大学习;B:背年学党史;C:中国梦宣传教育;D:社会主义核心价值观培育践行等一系列活动,学生可以任选一项参加.为了解参与情况,进行了一次抽样调查,根据收集的数据绘制了两幅不完整的统计图.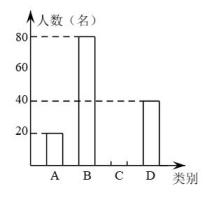
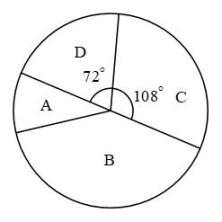
请根据图中提供的信息,解答下列问题:
(1)、在这次调查中,一共抽取了名学生;(2)、补全条形统计图;(3)、若该校共有学生1280名,请估计参加B项活动的学生数;(4)、小杰和小慧参加了上述活动,请用列表或画树状图的方法,求他们参加同一项活动的概率.21. 如图是直径,A是上异于C,D的一点,点B是延长线上一点,连接、、 , 且 .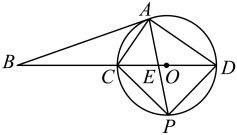 (1)、求证:直线是的切线;(2)、若 , 求的值;(3)、在(2)的条件下,作的平分线交于P,交于E,连接、 , 若 , 求的值.22. 如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为 , 点是其对称轴上一点,y轴上一点.
(1)、求证:直线是的切线;(2)、若 , 求的值;(3)、在(2)的条件下,作的平分线交于P,交于E,连接、 , 若 , 求的值.22. 如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为 , 点是其对称轴上一点,y轴上一点.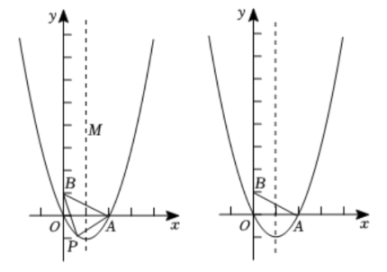 (1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.23. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.
(1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.23. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.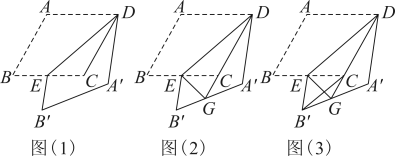 (1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.
(1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.