山东省枣庄市市中区2023年中考一模数学试题
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
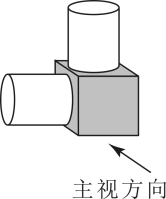
1. 如图所示的几何体的左视图是( )
 A、
A、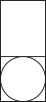 B、
B、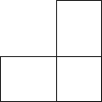 C、
C、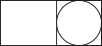 D、
D、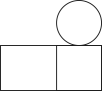 2. 如图, 中, , , .将 沿图示中的虚线剪开,按下面四种方式剪下的阴影三角形与原三角形相似的是( )
2. 如图, 中, , , .将 沿图示中的虚线剪开,按下面四种方式剪下的阴影三角形与原三角形相似的是( ) A、①②③ B、②③④ C、①② D、④3. 用配方法解方程 , 下列配方正确的是( )A、 B、 C、 D、4. 已知点A(1,-3)关于x轴的对称点在反比例函数的图像上,则实数k的值为( )A、3 B、 C、-3 D、5. 如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菜地内均匀地撒上种子,则种子落在阴影部分的概率是( )
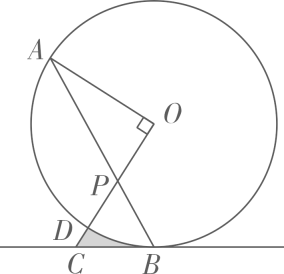
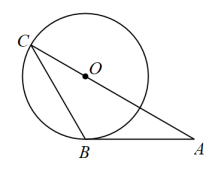
A、①②③ B、②③④ C、①② D、④3. 用配方法解方程 , 下列配方正确的是( )A、 B、 C、 D、4. 已知点A(1,-3)关于x轴的对称点在反比例函数的图像上,则实数k的值为( )A、3 B、 C、-3 D、5. 如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菜地内均匀地撒上种子,则种子落在阴影部分的概率是( )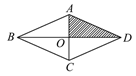 A、1 B、 C、 D、6. 如图,点A、B、C在⊙O上,BC OA,连接BO并延长,交⊙O于点D,连接AC,DC.若∠A=25°,则∠D的大小为( )
A、1 B、 C、 D、6. 如图,点A、B、C在⊙O上,BC OA,连接BO并延长,交⊙O于点D,连接AC,DC.若∠A=25°,则∠D的大小为( ) A、25° B、30° C、40° D、50°7. 如图,在边长相同的小正方形组成的网格中,点、、、都在这这些小正方形的顶点上,、相交于点 . 则的值是( )
A、25° B、30° C、40° D、50°7. 如图,在边长相同的小正方形组成的网格中,点、、、都在这这些小正方形的顶点上,、相交于点 . 则的值是( ) A、 B、 C、 D、8. 在平面直角坐标系中,已知点 , , 以原点为位似中心,相似比为 , 把缩小,则点的对应点的坐标是( )A、 B、 C、或 D、或9. 如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整自己的位置,设法使斜边保持水平,边与点B在同一直线上.已知直角三角纸板中 , , 测得眼睛D离地面的高度为 , 他与“步云阁”的水平距离为 , 则“步云阁”的高度是( )
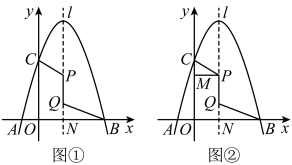
A、 B、 C、 D、8. 在平面直角坐标系中,已知点 , , 以原点为位似中心,相似比为 , 把缩小,则点的对应点的坐标是( )A、 B、 C、或 D、或9. 如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整自己的位置,设法使斜边保持水平,边与点B在同一直线上.已知直角三角纸板中 , , 测得眼睛D离地面的高度为 , 他与“步云阁”的水平距离为 , 则“步云阁”的高度是( )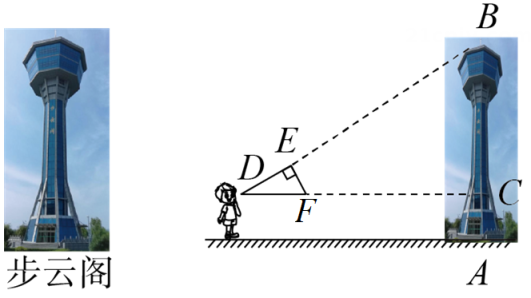 A、 B、 C、 D、10. 已知抛物线的对称轴是直线 , 其部分图象如图所示,下列说法中:①;②;③若、是抛物线上的两点,则有;④若m,n为方程的两个根,则且;以上说法正确的有( )
A、 B、 C、 D、10. 已知抛物线的对称轴是直线 , 其部分图象如图所示,下列说法中:①;②;③若、是抛物线上的两点,则有;④若m,n为方程的两个根,则且;以上说法正确的有( )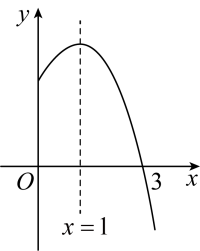 A、①②③④ B、②③④ C、②④ D、②③
A、①②③④ B、②③④ C、②④ D、②③二、填空题
-
11. 已知 , 则 .12. 如图,是的切线,为切点,的延长线交于点,连接 , 如果 , , 那么的长等于 .
 13. 已知关于x的一元二次方程(m﹣1)x2+2x+1=0有实数根,则m的取值范围是 .14. 如图,在中, , , , 是上一动点,过点作于点 , 于点 . 连接 , 则线段的最小值是 .
13. 已知关于x的一元二次方程(m﹣1)x2+2x+1=0有实数根,则m的取值范围是 .14. 如图,在中, , , , 是上一动点,过点作于点 , 于点 . 连接 , 则线段的最小值是 .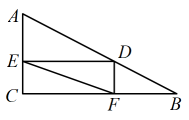 15. 如图,△ABO的顶点A在函数的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为 .
15. 如图,△ABO的顶点A在函数的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为 .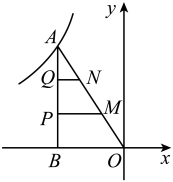 16. 如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF , 其中正确结论的序号是.
16. 如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF , 其中正确结论的序号是.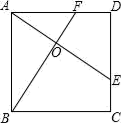
三、解答题
-
17.(1)、解方程;(2)、计算: .18. 如图,将①;②;③;④;⑤中的一个作为条件,另一个作为结论,组成一个真命题.
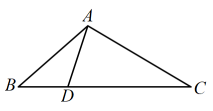 (1)、条件是 , 结论是;(注:填序号)(2)、写出你的证明过程.19. 为了培养学生的创新精神和实践能力,某校组织学生到技师学院开展了为期一周的社会实践活动.每位同学可以在“(机器人),(面塑),(电烙画),(摄影)”四门课程中选择一门.为公平起见,学校制作了如图所示的转盘,学生转动转盘一次,指针指到的课程即自己参加的实践课程.
(1)、条件是 , 结论是;(注:填序号)(2)、写出你的证明过程.19. 为了培养学生的创新精神和实践能力,某校组织学生到技师学院开展了为期一周的社会实践活动.每位同学可以在“(机器人),(面塑),(电烙画),(摄影)”四门课程中选择一门.为公平起见,学校制作了如图所示的转盘,学生转动转盘一次,指针指到的课程即自己参加的实践课程.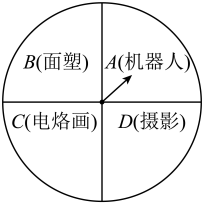 (1)、乐乐是该校的一名学生,乐乐参加“(摄影)”实践课程的概率是;(2)、果果和贝贝是好朋友,他们想参加相同的实践课程,请你用画树状图或列表的方法求他们参加相同实践课程的概率.(四门课程用所对应的字母表示)20. 如图①是一台手机支架,图②是其侧面示意图,、可分别绕点、转动,测量知 , . 当 , 转动到 , 时,求点到直线的距离.(精确到 , 参考数据: , , )
(1)、乐乐是该校的一名学生,乐乐参加“(摄影)”实践课程的概率是;(2)、果果和贝贝是好朋友,他们想参加相同的实践课程,请你用画树状图或列表的方法求他们参加相同实践课程的概率.(四门课程用所对应的字母表示)20. 如图①是一台手机支架,图②是其侧面示意图,、可分别绕点、转动,测量知 , . 当 , 转动到 , 时,求点到直线的距离.(精确到 , 参考数据: , , )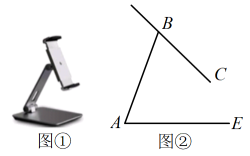 21. 如图,直线分别交轴、轴于、两点,与双曲线在第二象限内的交点为 , 轴于点 , 且 .
21. 如图,直线分别交轴、轴于、两点,与双曲线在第二象限内的交点为 , 轴于点 , 且 .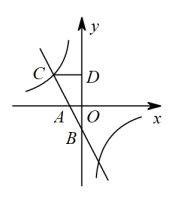 (1)、求双曲线的关系式;(2)、设点是双曲线上的一点,且的面积是的面积的4倍,求点的坐标.22. 如图,菱形的对角线 , 相交于点 , 于点 , 是的中点,于点 .
(1)、求双曲线的关系式;(2)、设点是双曲线上的一点,且的面积是的面积的4倍,求点的坐标.22. 如图,菱形的对角线 , 相交于点 , 于点 , 是的中点,于点 .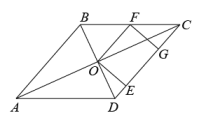 (1)、求证:四边形是矩形;(2)、若 , , 求的值.
(1)、求证:四边形是矩形;(2)、若 , , 求的值.