山东省青岛市西海岸新区2023年中考一模数学试题
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
1. 低碳环保理念深入人心,共享单车已成为出行新方式.下列共享单车图标,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 近年来,我国能源保供稳价政策有力推进.其中2022年1—11月份,我国生产原煤40.9亿吨.40.9亿用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、-(2x2)3=8x6 B、x5÷x2=x3 C、3x2×2x3=6x6 D、4. 将两本相同的书进行叠放,得到如图所示的几何体,则它的主视图是( )
2. 近年来,我国能源保供稳价政策有力推进.其中2022年1—11月份,我国生产原煤40.9亿吨.40.9亿用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、-(2x2)3=8x6 B、x5÷x2=x3 C、3x2×2x3=6x6 D、4. 将两本相同的书进行叠放,得到如图所示的几何体,则它的主视图是( )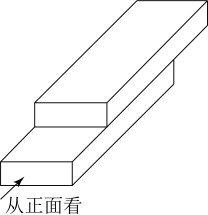 A、
A、 B、
B、 C、
C、 D、
D、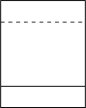 5. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
5. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )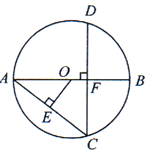 A、9.6 B、4 C、5 D、106. 某中学篮球队12名队员的年龄情况如下表,则这个队队员年龄的众数和中位数分别( )
A、9.6 B、4 C、5 D、106. 某中学篮球队12名队员的年龄情况如下表,则这个队队员年龄的众数和中位数分别( )年龄(岁)
14
15
16
17
18
人数(人)
1
4
3
2
2
A、15,16 B、15,15 C、15,15.5 D、16,157. 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB= , ∠C=120°,则点B′的坐标为( )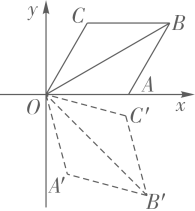 A、(3,) B、(3,-) C、( , ) D、( , -)8. 如图,是抛物线 ( )图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线 ( )与抛物线交于A,B两点,下列结论:① ; ②抛物线与x轴的另一个交点是( ,0);③方程 有两个相等的实数根;④当时 ,有 ;⑤若 ,且 ;则 .则命题正确的个数为( )
A、(3,) B、(3,-) C、( , ) D、( , -)8. 如图,是抛物线 ( )图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线 ( )与抛物线交于A,B两点,下列结论:① ; ②抛物线与x轴的另一个交点是( ,0);③方程 有两个相等的实数根;④当时 ,有 ;⑤若 ,且 ;则 .则命题正确的个数为( )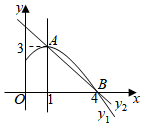 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
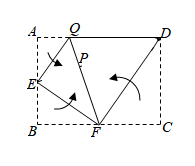
9. 若 , 则= .10. 某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送三”促销活动,即整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元,则该品牌饮料一箱有瓶.11. 如图,在矩形ABCD中,E,F分别是边AB,BC上的点.将∠A,∠B,∠C按如图所示的方式向内翻折,EQ,EF,DF为折痕.若A,B,C恰好都落在同一点P上,AE=1,则ED=.
 12. 如图,在平面直角坐标系中,矩形的顶点A,C分别在x轴,y轴的正半轴上,反比例函数的图象交于点D,交于点E.若 , , 则的值为 .
12. 如图,在平面直角坐标系中,矩形的顶点A,C分别在x轴,y轴的正半轴上,反比例函数的图象交于点D,交于点E.若 , , 则的值为 .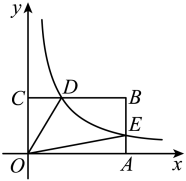 13. 如图,在扇形AOB中,点C在线段OB上,连接AC,将△AOC沿AC所在直线翻折,使得点O的对应点D恰好落在上,若OA=2,则图中阴影部分的面积为 .
13. 如图,在扇形AOB中,点C在线段OB上,连接AC,将△AOC沿AC所在直线翻折,使得点O的对应点D恰好落在上,若OA=2,则图中阴影部分的面积为 .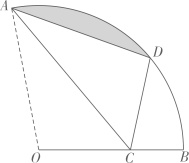 14. 如图,在轴的正半轴上依次截取 , 过点 , , , , 分别作轴的垂线与反比例函数的图像相交于点 , , , , , 得直角三角形 , , , , , 并设其面积分别为 , , , , , 则 .
14. 如图,在轴的正半轴上依次截取 , 过点 , , , , 分别作轴的垂线与反比例函数的图像相交于点 , , , , , 得直角三角形 , , , , , 并设其面积分别为 , , , , , 则 .
三、解答题
-
15. 已知:及其一边上的两点A,B.求作:平行四边形 , 使点C到两边的距离相等.
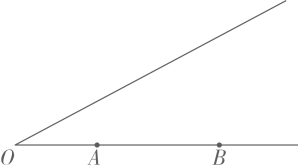 16. 计算:(1)、化简:;(2)、解不等式组: , 并写出它的最大整数解.17. 为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),其中A组: , B组: , C组: , D组: , E组: , 并绘制了如下不完整的统计图.
16. 计算:(1)、化简:;(2)、解不等式组: , 并写出它的最大整数解.17. 为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),其中A组: , B组: , C组: , D组: , E组: , 并绘制了如下不完整的统计图.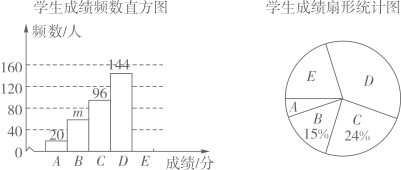 (1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中 , 扇形统计图中A组占;(2)、补全学生成绩频数分布直方图;(3)、若将竞赛成绩在90分及以上的记为优秀,求优秀学生所在扇形对应圆心角的度数.18. 圆周率 是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对 有过深入的研究.目前,超级计算机已计算出 的小数部分超过31.4万亿位.有学者发现,随着 小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中 , 扇形统计图中A组占;(2)、补全学生成绩频数分布直方图;(3)、若将竞赛成绩在90分及以上的记为优秀,求优秀学生所在扇形对应圆心角的度数.18. 圆周率 是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对 有过深入的研究.目前,超级计算机已计算出 的小数部分超过31.4万亿位.有学者发现,随着 小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
 (1)、从 的小数部分随机取出一个数字,估计数字是6的概率为;(2)、某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)19. 重庆市某校数学兴趣小组在水库某段的附近借助无人机进行实物测量的社会实践活动.如图所示,兴趣小组在水库正面左岸的处测得水库右岸处某标志物顶端的仰角为 . 在处一架无人飞机以北偏西方向飞行米到达点处,无人机沿水平线方向继续飞行30米至处,测得正前方水库右岸处的俯角为 . 线段的长为无人机距地面的铅直高度,点、、在同一条直线上.
(1)、从 的小数部分随机取出一个数字,估计数字是6的概率为;(2)、某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)19. 重庆市某校数学兴趣小组在水库某段的附近借助无人机进行实物测量的社会实践活动.如图所示,兴趣小组在水库正面左岸的处测得水库右岸处某标志物顶端的仰角为 . 在处一架无人飞机以北偏西方向飞行米到达点处,无人机沿水平线方向继续飞行30米至处,测得正前方水库右岸处的俯角为 . 线段的长为无人机距地面的铅直高度,点、、在同一条直线上.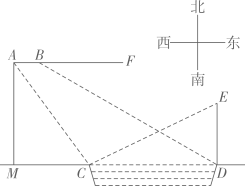 (1)、求无人机的飞行高度;(2)、求标志物的高度.(结果精确到0.1米)
(1)、求无人机的飞行高度;(2)、求标志物的高度.(结果精确到0.1米)(已知数据: , , , , , , )
20. 在学校开展“劳动创造美好生活”主题系列活动中,八年级(1)班负责校园某绿化角的设计、种植与养护.同学们约定每人养护一盆绿植,计划购买绿萝和吊兰两种绿植共46盆,且绿萝盆数不少于吊兰盆数的2倍.已知绿萝每盆9元,吊兰每盆6元.(1)、采购组计划将预算经费390元全部用于购买绿萝和吊兰,问可购买绿萝和吊兰各多少盆?(2)、规划组认为有比390元更省钱的购买方案,请求出购买两种绿植总费用的最小值.21. 【探究函数的图象与性质】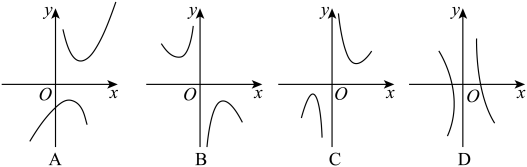 (1)、函数的自变量x的取值范围是;(2)、下列四个函数图象中,函数的图象大致是;(3)、对于函数 , 求当时,y的取值范围.请将下列的求解过程补充完整.
(1)、函数的自变量x的取值范围是;(2)、下列四个函数图象中,函数的图象大致是;(3)、对于函数 , 求当时,y的取值范围.请将下列的求解过程补充完整.解:∵ , ∴ .
∵ , ∴ .
(4)、【拓展说明】若函数 , 求y的取值范围.
22. 如图,点C是 的中点,四边形 是平行四边形.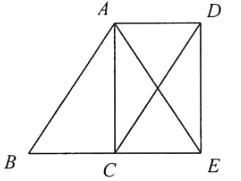 (1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.23. 如图,抛物线与轴相交于点 , 与轴相交于点 .
(1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.23. 如图,抛物线与轴相交于点 , 与轴相交于点 .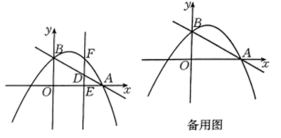 (1)、求抛物线的表达式.(2)、为线段上一点(不与点 , 重合),过点作轴于点 , 交抛物线于点 , 若 , 求点的坐标.(3)、是第四象限内抛物线上一点,已知 , 则点的坐标为 .24. 某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线 表示墙面,已知 , 米, 米)和总长为36米的篱笆围建一个“日”形的饲养场 (细线表示篱笆,饲养场中间 也是用篱笆隔开),如图,点 可能在线段 上,也可能在线段 的延长线上.
(1)、求抛物线的表达式.(2)、为线段上一点(不与点 , 重合),过点作轴于点 , 交抛物线于点 , 若 , 求点的坐标.(3)、是第四象限内抛物线上一点,已知 , 则点的坐标为 .24. 某牧场准备利用现成的一堵“7”字型的墙面(如图中粗线 表示墙面,已知 , 米, 米)和总长为36米的篱笆围建一个“日”形的饲养场 (细线表示篱笆,饲养场中间 也是用篱笆隔开),如图,点 可能在线段 上,也可能在线段 的延长线上.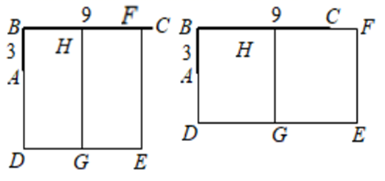 (1)、当点 在线段 上时,
(1)、当点 在线段 上时,①设 的长为 米,则 ▲ 米(用含 的代数式表示);
②若要求所围成的饲养场 的面积为66平方米,求饲养场的宽 ;
(2)、饲养场的宽 为多少米时,饲养场 的面积最大?最大面积为多少平方米?25. 如图,在平面直角坐标系中,矩形的其中两边分别在坐标轴上,它的两条对角线交于点E,其中 , , 动点M从点C出发,以的速度在上向点B运动,动点N同时从点B出发,以的速度在上向点O运动.当其中一个动点到达终点时,它们同时停止运动.设它们运动时间是 .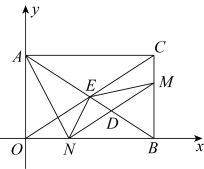 (1)、请直接写出的长度;(2)、当t为何值时,与相似;(3)、记的面积为S,求出S与t的函数表达式,并求出S的最小值及此时t的值.
(1)、请直接写出的长度;(2)、当t为何值时,与相似;(3)、记的面积为S,求出S与t的函数表达式,并求出S的最小值及此时t的值.