山东省聊城东昌府区2023年中考一模数学试题

试卷更新日期：2023-04-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 2023的相反数的倒数是（）

A、2023 B、-2023 C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. 如图所示的几何体是由五个小正方体组合而成的，它的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $a^{8} \div a^{4} = a^{2}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(a^{4})}^{- 3} = a^{- 12}$ D、 $\sqrt{a^{2}} = a$

查看试题解析
4. 如图，在 $△ A B C$ 中， $∠ A = 75 °$ ，若 $∠ A B D = 105 °$ ，过点C作 $C E ∥ B D$ ，则 $∠ A C E$ 的度数为（）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $35 °$

查看试题解析
5. 某市举行“学雷锋见行动”青少年演讲比赛，时代中学要从甲、乙、丙、丁四位同学中选一名同学参加，下表是这四名同学五次校演讲比赛成绩统计表，如果从这四位同学中，选出一位同学参赛，那么应选的同学是（）

甲
乙
丙
丁
平均分
85
90
90
85
方差
50
42
50
42

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 不等式组 ${\begin{array}{l} x + 5 < 4 x - 1 \\ \frac{3}{2} x \leq 6 - \frac{1}{2} x \end{array}$ 的解集是（）

A、 $x ≥ 3$ B、 $x < 2$ 或 $x ≥ 3$ C、 $x < 2$ D、 $2 < x \leq 3$

查看试题解析
7. 在平面直角坐标系中点 $A (3 ， 2)$ 关于x轴的对称点为 $A_{1}$ ， $A_{1}$ 关于原点的对称点为 $A_{2}$ ，则点 $A_{2}$ 的坐标是（）

A、 $(- 3 ， 2)$ B、 $(3 ， - 2)$ C、 $(- 2 ， - 3)$ D、 $(- 3 ， - 2)$

查看试题解析
8. 下列计算正确的是（）

A、 $3 + 4 \sqrt{2} = 7 \sqrt{2}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $\sqrt{3} \div \frac{1}{\sqrt{6}} = 2 \sqrt{3}$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C$ ，三个顶点A，B，C均在 $⊙ O$ 上， $B D$ 过圆心O，连接 $A D$ ．当 $∠ O B C = 40 °$ 时， $∠ A D B$ 的度数是（）

A、45° B、55° C、65° D、75°

查看试题解析
10. 一元二次方程 $2 x^{2} - 3 x + 1 = 0$ 配方后可化为（）

A、 ${(x - \frac{3}{4})}^{2} = 1$ B、 ${(x - \frac{3}{4})}^{2} = \frac{9}{16}$ C、 ${(x - \frac{3}{4})}^{2} = \frac{1}{4}$ D、 ${(x - \frac{3}{4})}^{2} = \frac{1}{16}$

查看试题解析
11. 如图，已知 $R t △ A B C$ 的 $∠ A = 90 °$ ， $A B = A C = 4$ ，以点 $B$ 为圆心， $B A$ 为半径，作 $\overset{⌢}{A E}$ 交 $B C$ 于点 $E$ ．若扇形 $A B E$ 恰好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{2}}{2}$ D、 $\sqrt{2}$

查看试题解析
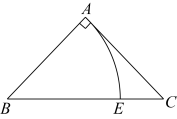12. 如图，在等腰直角 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = C B = 8 c m$ ，点O为斜边 $A B$ 的中点，连接 $O C$ ，点E，F分别从A，C两点同时出发，以 $1 c m / s$ 的速度沿 $A \to C$ ， $C \to B$ 运动，到点C，B时停止运动．设运动时间为 $t (s)$ ， $△ O E F$ 的面积为 $s (c m^{2})$ ，则 $s (c m^{2})$ 与 $t (s)$ 的函数关系可用图象表示为（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 因式分解： $3 x^{2} + 3 y^{2} - 6 x y =$ ．

查看试题解析
14. 一元二次方程 $k x^{2} + 2 (k - 1) x + k = 0$ 有两个不相等的实数根，则k的取值范围为．

查看试题解析
15. 如图， $△ A^{'} B^{'} C$ 是将 $△ A B C$ 绕点C顺时针旋转，使点B旋转后的对应点 $B^{'}$ 落在边 $A B$ 上时得到的，边 $A C$ 与 $A^{'} B^{'}$ 交于点D，若 $∠ A = 28 °$ ， $∠ B = 63 °$ ，则 $∠ A^{'} D A =$ ．

查看试题解析
16. 汽车行驶到某一十字路口有三种等可能性的选择：直行、左转、右转．两辆由南向北行驶的汽车在同时经过该十字路口后，反向行驶的概率是．

查看试题解析
17. 如图，已知 $O A_{1} = 1$ ，以 $O A_{1}$ 为直角边作 $R t △ O A_{1} A_{2}$ ，并使 $∠ A_{1} O A_{2} = 60 °$ ，再以 $O A_{2}$ 为直角边作 $R t △ O A_{2} A_{3}$ ，并使 $∠ A_{2} O A_{3} = 60 °$ ，再以 $O A_{3}$ 为直角边作 $R t △ O A_{3} A_{4}$ ，并使 $∠ A_{3} O A_{4} = 60 °$ ， …按此规律进行下去，则 $R t △ O A_{2022} A_{2023}$ 的直角边 $A_{2022} A_{2023}$ 的长为．

查看试题解析

三、解答题

18. 先化简，再求值： $1 - (x + 1 - \frac{2 x - 1}{x - 1}) \div \frac{x^{2} - 2 x}{x^{2} - 1}$ ，其中 $x = c o s 30 ° + t a n 60 °$ ．

查看试题解析
19. 为了更好地打造生态文明城，桃源社区计划用公益基金购进甲、乙两种体育器材供市民锻炼身体．调查发现：若购买甲种体育器材3个，乙种体育器材2个，共需要资金1.2万元；若购买甲种体育器材4个，乙种体育器材3个，共需要资金1.7万元．

(1)、甲、乙两种体育器材的单价分别是多少万元？

(2)、若该社区计划购进这两种体育器材共20个，而最多提供公益基金4.8万元，甲种体育器材至少购进多少个？

查看试题解析
20. 为开展学习宣传贯彻党的二十大精神活动，某中学就有关“党的二十大精神”的了解程度，采取随机抽样的方式抽取本校部分学生进行了测试（满分100分），并将测试成绩进行了收集整理，绘制了如下不完整的统计图、表．
成绩等级
分数段
频数（人数）
优秀
$90 \leq x \leq 100$
a
良好
$80 \leq x \leq 90$
b
较好
$70 \leq x < 80$
12
一般
$60 \leq x < 70$
10
较差
$x < 60$
3
请根据统计图、表中所提供的信息，解答下列问题：

(1)、统计表中的 $a =$ ， $b =$ ；成绩扇形统计图中“良好”所在扇形的圆心角是度；

(2)、补全上面的成绩条形统计图；

(3)、若该校共有学生2400人，估计该校学生对“党的二十大精神”的了解程度达到良好以上（含良好）的人数．

查看试题解析
21. 某数学兴趣小组去测量一座小山的高度，在小山顶上有一高度为20米的发射塔 $A B$ ，如图所示，在山脚平地上的D处测得塔底B的仰角为 $30 °$ ，向小山前进80米到达点E处，测得塔顶A的仰角为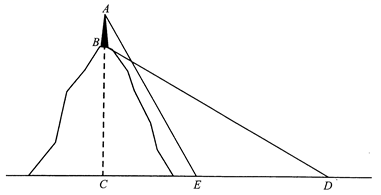 $60 °$ ，求小山 $B C$ 的高度．

查看试题解析
22. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ，过A点作 $A E ⊥ C D$ 交 $B C$ 的延长线于点F，且 $C E = D E$ ，连接 $D F ， A C$ ．

(1)、求证：四边形 $A C F D$ 是菱形；

(2)、若 $A E = \sqrt{3}$ ， $∠ B A C = 75 °$ ， $∠ A D E = 60 °$ ，求 $B F$ 的长．

查看试题解析
23. 如图，直线 $A B$ 与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于A，B两点，过点A作 $A C ∥ x$ 轴，过点B作 $B C ∥ y$ 轴， $A C ， B C$ 交于点 $C (2 ， 3)$ ，且 $A C$ 交y轴于点D，连接 $B D$ ．

(1)、当 $S_{△ A B C} = \frac{3}{4}$ 时，求此时点A，B的坐标；

(2)、当k为何值时， $△ A B D$ 的面积最大，最大面积是多少？

查看试题解析
24. 如图，以等腰 $△ A B C$ 的腰 $A B$ 为直径作 $⊙ O$ ，交底边 $B C$ 于点D，过点D作 $D G ⊥ A C$ 于点G，延长 $C A$ 交 $⊙ O$ 于点E，连接 $D E$ ，交 $A B$ 于点F．

(1)、求证： $D G$ 是圆O的切线；

(2)、若 $E A = E F = 1$ ，求圆O的半径．

查看试题解析
25. 如图，已知抛物线 $y = a x^{2} + 2 x + c$ 交x轴于点 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ ，交y轴于点C，点D与点C关于抛物线的对称轴对称．

(1)、求该抛物线的表达式，并求出点D的坐标；

(2)、若点E为该抛物线上的点，点F为直线 $A D$ 上的点，若 $E F ∥ x$ 轴，且 $E F = 1$ （点E在点F左侧），求点E的坐标；

(3)、若点P是该抛物线对称轴上的一个动点，是否存在点P，使得 $△ A P D$ 为直角三角形？若不存在，请说明理由；若存在，直接写出点P坐标．

查看试题解析

成绩等级	分数段	频数（人数）
优秀	$90 \leq x \leq 100$	a
良好	$80 \leq x \leq 90$	b
较好	$70 \leq x < 80$	12
一般	$60 \leq x < 70$	10
较差	$x < 60$	3

	甲	乙	丙	丁
平均分	85	90	90	85
方差	50	42	50	42