山东省济南市市中区2023年中考一模数学试题

试卷更新日期：2023-04-24 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的绝对值是（）

A、-3 B、3 C、 $\pm \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
2. 如图是由七个完全相同的小正方体组成的立体图形，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 在今年的全国两会报道中，央视新闻频道首次把央视新闻新媒体平台作为报道主战场，重点打造“V观两会”微视频和“云直播”，以独特的优势引领媒体两会报道工作。截至3月15日，央视新闻新媒体各平台两会报道阅读总量突破3900000000，请将数据3900000000用科学记数法表示为（）

A、 $3.9 \times 1 0^{9}$ B、 $0.39 \times 1 0^{9}$ C、 $3.9 \times 1 0^{10}$ D、 $0.39 \times 1 0^{10}$

查看试题解析
4. 如图，将一块直角三角板的直角顶点放在直尺的一边上.若∠2＝40°，则∠1的度数是（）

A、60° B、50° C、40° D、30°

查看试题解析
5. 下列运算正确的是（）

A、 $a^{2} + 2 a^{2} = 3 a^{4}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(2 a^{2})}^{3} = 8 a^{6}$ D、 $(a - b)^{2} = a^{2} - b^{2}$

查看试题解析
6. 下列图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 实数a，b在数轴上对应的点的位置如图所示，下列结论正确的是（）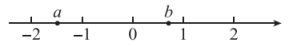

A、 $a > b$ B、 $- a < b$ C、 $| a | < | b |$ D、 $a + b < 0$

查看试题解析
8. 如图，一只松鼠先经过第一道门（A，B或C），再经过第二道门（D或E）出去，则松鼠走出笼子的路线是“先经过A门，再经过E门”的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{5}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = B C$ ，以B为圆心，适当长为半径画弧交 $B A$ 于点M，交 $B C$ 于点N，分别以M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧相交于点D，射线 $B D$ 交 $A C$ 于点E，点F为 $B C$ 的中点，连接 $E F$ ，若 $B E = A C = 4$ ，则 $△ C E F$ 的周长是（）

A、8 B、 $2 \sqrt{3} + 2$ C、 $2 \sqrt{5} + 6$ D、 $2 \sqrt{5} + 2$

查看试题解析
10. 已知二次函数 $y = - x^{2} + x + m^{2} (m > 0)$ 与一次函数 $y = - x + 1$ 交于 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 两点 $(x_{1} < x_{2})$ ，当 $x_{1} \leq x \leq x_{2}$ 时，至少存在一个x使得 $- x^{2} + x + m^{2} \geq \frac{1}{3}$ 成立，则m的取值范围是（）

A、 $0 < m \leq \frac{1}{5}$ B、 $\frac{1}{5} \leq m \leq \frac{1}{4}$ C、 $\frac{1}{4} \leq m \leq \frac{1}{3}$ D、 $m \geq \frac{1}{3}$

查看试题解析

二、填空题

11. 分解因式： $a^{2} - a b$ = ．

查看试题解析
12. 下图是由全等的小正方形组成的图案，假设可以随意在图中取点，那么这个点取在阴影部分的概率是.

查看试题解析
13. 代数式 $\frac{2}{x - 4}$ 与代数式 $\frac{3}{x - 8}$ 的值相等，则 $x =$ ．

查看试题解析
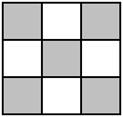14. 如图，在边长为2的正方形ABCD中，对角线AC的中点为O，分别以点A，C为圆心，以AO的长为半径画弧，分别与正方形的边相交，则图中的阴影部分的面积为.（结果保留π）

查看试题解析
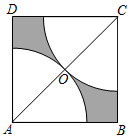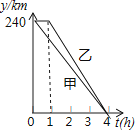
15.
在一条笔直的公路上有A，B，C三地，C地位于A，B两地之间，甲，乙两车分别从A，B两地出发，沿这条公路匀速行驶至C地停止．从甲车出发至甲车到达C地的过程，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图表示，当甲车出发h时，两车相距350km．

查看试题解析
16. 如图，点O是正方形 $A B C D$ 的中心， $A B = 3 \sqrt{2}$ ． $R t △ B E F$ 中， $∠ B E F = 90 °$ ， $E F$ 过点D． $B E ， B F$ 分别交 $A D ， C D$ 于点G、M，连接 $O E ， O M ， E M$ ．若 $B G = D F$ ， $t a n ∠ A B G = \frac{1}{3}$ ，则 $E M$ 的长．

查看试题解析

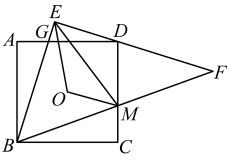
三、解答题

17. 计算： ${(\frac{1}{2})}^{- 1} - 4 c o s 45 ° + {(\frac{π}{3})}^{0} - \sqrt{9}$

查看试题解析
18. 解不等式组： ${\begin{array}{l} 3 (x - 1) < 2 x ， \\ \frac{5 x + 3}{2} > x ， \end{array}$ 并写出所有整数解．

查看试题解析
19. 如图，在▱ABCD中，点E，F是对角线AC上的两点，且AF=CE，连接DE，BF.求证：DE∥BF.

查看试题解析

20. 某校举行了冬奥会知识竞赛，在全校随机抽取了部分学生的竞赛成绩进行整理和分析（成绩得分用x表示，共分成四组），并绘制成如下的竞赛成绩分组统计表和扇形统计图．其中“

60 \leq x < 70

”，“

70 \leq x < 80

”这两组数据如下：61，74，68，62，73，70，72，78，69，74，79，68，74．

竞赛成绩分组统计表

组别	竞赛成绩分组	频数
1	$60 \leq x < 70$	a
2	$70 \leq x < 80$	b
3	$80 \leq x < 90$	$12$
4	$90 \leq x < 100$	d

请根据以上信息，解答下列问题：

(1)、填空：

a =

；

(2)、统计图中第四组对应圆心角为度；

(3)、“

70 \leq x < 80

”这组数据的众数是，中位数是；

(4)、若学生竞赛成绩达到90分及以上获奖，请你估计全校1200名学生中获奖的人数．

查看试题解析

21. 2022年举世瞩目的北京冬奥会的成功举办掀起了全民冰雪运动的热潮．图1、图2分别是一名滑雪运动员在滑雪过程中某一时刻的实物图与示意图，已知运动员的小腿 $E D$ 与斜坡 $A B$ 垂直，大腿 $E F$ 与斜坡 $A B$ 平行，G为头部，假设G，E，D三点共线且头部到斜坡的距离 $G D$ 为 $1.05 m$ ，上身与大腿夹角 $∠ G F E = 53 °$ ，膝盖与滑雪板后端的距离 $E M$ 长为 $0.9 m$ ， $∠ E M D = 30 °$

(1)、求此滑雪运动员的小腿 $E D$ 的长度；

(2)、求此运动员的身高．（运动员身高由 $G F 、 E F 、 D E$ 三条线段构成；参考数据： $s i n 53 ° \approx \frac{4}{5}$ ， $c o s 53 ° \approx \frac{3}{5}$ ， $t a n 53 ° \approx \frac{4}{3}$ ）

查看试题解析
22. 如图， $B C$ 是 $⊙ O$ 的直径， $C E$ 是 $⊙ O$ 的弦，过点 $E$ 作 $⊙ O$ 的切线，交 $C B$ 的延长线于点 $G$ ，过点 $B$ 作 $B F ⊥ G E$ 于点 $F$ ，交 $C E$ 的延长线于点 $A$ ．

(1)、求证： $∠ A B G = 2 ∠ C$ ；

(2)、若 $G F = 3 \sqrt{3}$ ， $G B = 6$ ，求 $⊙ O$ 的半径．

查看试题解析
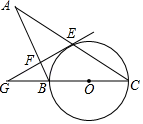23. 某校艺术节，计划购买红、蓝两种颜色的文化衫进行手绘设计，并进行义卖后将所获利润全部捐给山区困难孩子．已知该学校从批发市场花4800元购买了红、蓝两种颜色的文化衫220件，每件文化衫的批发价及手绘后的零售价如表：

批发价（元）
零售价（元）
红色文化衫
25
45
蓝色文化衫
20
35

(1)、学校购进红、蓝文化衫各几件？

(2)、若学校再次购进红、蓝两种颜色的文化衫300件，其中红色文化衫的数量不多于蓝色文化衫数量的2倍，请设计一个方案：学校购进红色文化衫多少件时获得最大利润，最大利润是多少？

查看试题解析
24. 已知在等腰直角三角形 $△ A B C$ 中， $∠ B = 90 °$ ， $A (0 ， 2)$ ， $B (1 ， 0)$ ．

(1)、如图1，请直接写出点C的坐标，若点C在反比例函数 $y = \frac{k_{1}}{x} (x > 0)$ 上，则 $k_{1} =$ ；

(2)、如图2，若将 $△ A B C$ 延x轴向右平移得到 $△ A^{'} B^{'} C^{'}$ ，平移距离为m，当 $A^{'}$ ， $C^{'}$ 都在反比例函数 $y = \frac{k_{2}}{x} (x > 0)$ 上时，求 $k_{2}$ ， m；

(3)、如图3，在（2）的条件下，在y轴上是否存在点P，使得 $△ B^{'} C^{'} P$ 的面积是 $△ A^{'} B^{'} C^{'}$ 面积的一半．若存在，请求出点P；若不存在，请说明理由．

查看试题解析
25. 如图

(1)、①如图1，等腰 $△ A B C$ （ $B C$ 为底）与等腰 $△ A D E$ （ $D E$ 为底）， $∠ B A C = ∠ D A E$ ，则 $B D$ 与 $C E$ 的数量关系为；
②如图2，矩形 $A B C D$ 中， $A B = 3$ ， $A D = 4$ ，则 $s i n ∠ D A C =$ ；

(2)、如图3，在（1）②的条件下，点 $E$ 在线段 $C D$ 上运动，将 $A E$ 绕点 $A$ 顺时针旋转得到 $A F$ ，使 $∠ E A F = ∠ D A C$ ，连接 $C F$ ．当 $A E = 3 \sqrt{2}$ 时，求 $C F$ 的长度；

(3)、如图4，矩形 $A B C D$ 中，若 $A B = 2 \sqrt{3}$ ， $A D = 6$ ，点 $E$ 在线段 $C D$ 上运动，将 $A E$ 绕点 $A$ 顺时针旋转得到 $A F$ ，旋转角等于 $∠ B A C$ ，连结 $C F ， A E$ 中点为 $G ， C F$ 中点为 $H$ ，若 $G H = \sqrt{13}$ ，直接写出 $D E$ 的长．

查看试题解析
26. 图1，在平面直角坐标系 $x O y$ 中，已知抛物线 $y = - x^{2} + b x + c$ 经过 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点．P是抛物线上一点，且在直线 $B C$ 的上方．

(1)、求抛物线的解析式；

(2)、如图2，点E为 $O C$ 中点，作 $P Q ∥ y$ 轴交 $B C$ 于点Q，若四边形 $C P Q E$ 为平行四边形，求点P的横坐标；

(3)、如图3，连结 $A C 、 A P$ ， $A P$ 交 $B C$ 于点M，作 $P H ∥ A C$ 交 $B C$ 于点H．记 $△ P H M$ ， $△ P M C$ ， $△ C A M$ 的面积分别为 $S_{1} ， S_{2} ， S_{3}$ ．判断 $\frac{S_{1}}{S_{2}} + \frac{S_{2}}{S_{3}}$ 是否存在最大值，若存在，求出最大值；若不存在，请说明理由．

查看试题解析

	批发价（元）	零售价（元）
红色文化衫	25	45
蓝色文化衫	20	35