辽宁省鞍山市立山区2023年九年级中考二模数学试题
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
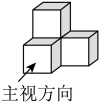
1. 四个相同的小正方形组成的立体图形如图所示,它的主视图为( )
 A、
A、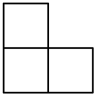 B、
B、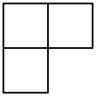 C、
C、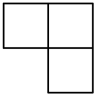 D、
D、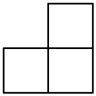 2. 若关于x的一元二次方程的一个根为0,则m的值为( )A、-2 B、0 C、2 D、-2或23. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ).
2. 若关于x的一元二次方程的一个根为0,则m的值为( )A、-2 B、0 C、2 D、-2或23. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ). A、 B、 C、 D、4. 如图,电路图上有 个开关 、 、 、 和 个小灯泡,同时闭合开关 、 或同时闭合开关 、 都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A、 B、 C、 D、4. 如图,电路图上有 个开关 、 、 、 和 个小灯泡,同时闭合开关 、 或同时闭合开关 、 都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )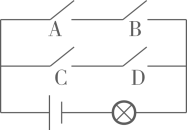 A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关5. 如图,已知点C,D是以为直径的半圆O的三等分点,弧的长为 , 则图中阴影部分的面积为( )
A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关5. 如图,已知点C,D是以为直径的半圆O的三等分点,弧的长为 , 则图中阴影部分的面积为( )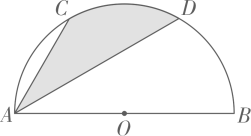 A、 B、 C、 D、6. 如图,点A是反比例函数y (x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y= 的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A、 B、 C、 D、6. 如图,点A是反比例函数y (x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y= 的图象于点B,点P是x轴上的动点,则△PAB的面积为( )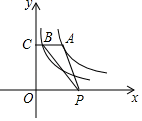 A、2 B、4 C、6 D、87. 如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为 , 且三角板的一边长为 . 则投影三角板的对应边长为( )
A、2 B、4 C、6 D、87. 如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为 , 且三角板的一边长为 . 则投影三角板的对应边长为( )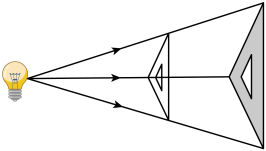 A、 B、 C、 D、8. 如图,在矩形 中, , ,动点P , Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P , Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接 .设点P的运动路程为x , 为y , 则y关于x的函数图象大致是( )
A、 B、 C、 D、8. 如图,在矩形 中, , ,动点P , Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P , Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接 .设点P的运动路程为x , 为y , 则y关于x的函数图象大致是( )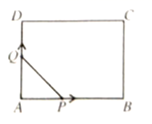 A、
A、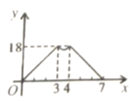 B、
B、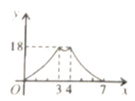 C、
C、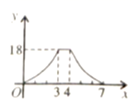 D、
D、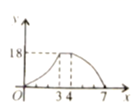
二、填空题
-
9. 目前以等为代表的战略性新兴产业蓬勃发展.某市2021年底有用户2万户,计划到2023年底全市用户数累计达到8.72万户.设全市用户数年平均增长率为 , 则根据题意可列方程为 .10. 如图,在 中, ,将 绕点 按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为 .
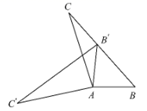 11. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值为.12. 如图,圆锥的母线 , 侧面展开图是半圆,则底面半径 .13. 一个不透明的箱子里装有个球,其中红球有3个,这些球除颜色外都相同,每次将箱子里的球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出的值为 .14. 如图,在矩形中, , 点是边上一点,连接相交于点 , 连接 , 若 , 则 .
11. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值为.12. 如图,圆锥的母线 , 侧面展开图是半圆,则底面半径 .13. 一个不透明的箱子里装有个球,其中红球有3个,这些球除颜色外都相同,每次将箱子里的球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出的值为 .14. 如图,在矩形中, , 点是边上一点,连接相交于点 , 连接 , 若 , 则 .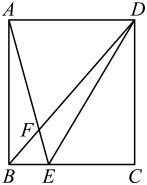 15. 如图,已知反比例函数的图象经过的顶点 , 点在轴负半轴,点在轴正半轴,交轴于点 , 交轴于点 , 若 , . 则 .
15. 如图,已知反比例函数的图象经过的顶点 , 点在轴负半轴,点在轴正半轴,交轴于点 , 交轴于点 , 若 , . 则 .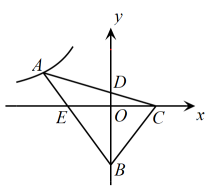 16. 如图,直线与轴交于点 , 点在轴正半轴上且横坐标分别为2,4,6,…,过作轴交直线于点 , 连接 , , 且交于点;过作轴交直线于点 , 连接 , , 且交于点;…按照此规律进行下去,则的纵坐标为 .
16. 如图,直线与轴交于点 , 点在轴正半轴上且横坐标分别为2,4,6,…,过作轴交直线于点 , 连接 , , 且交于点;过作轴交直线于点 , 连接 , , 且交于点;…按照此规律进行下去,则的纵坐标为 .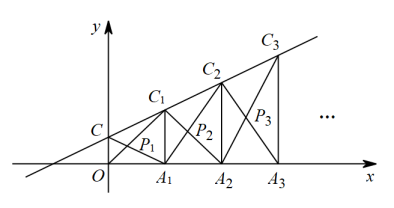
三、解答题
-
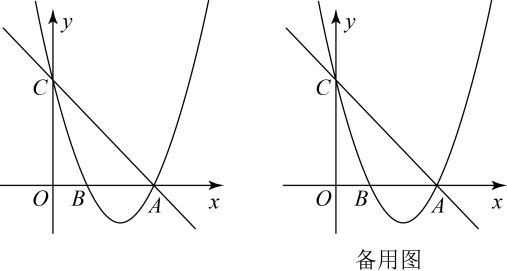
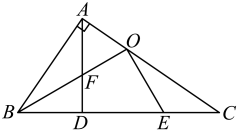
17. 已知关于x的一元二次方程 .(1)、求证:无论k为何实数,方程总有两个不相等的实数根;(2)、若方程的两个实数根 , 满足 ,求k的值.18. 如图,在中, , 于点 , 点是边上一点,连接交于 , 交边于点 . 求证: .
 19. 如图,一次函数的图象与反比例函数的图象相交于两点(A在的右侧).
19. 如图,一次函数的图象与反比例函数的图象相交于两点(A在的右侧).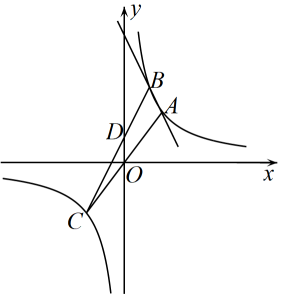 (1)、若 , 求反比例函数解析式;(2)、连接并延长交反比例函数图象的另一分支于点 , 连接交轴于点 , 若 , 求的面积.20. 小红的爸爸积极参加社区志愿服务工作.根据社区安排,志愿者被随机分到组(清除小广告)、组(便民代购)和组(环境消杀).(1)、小红爸爸被分到组的概率是;(2)、某中学王老师也参加了该社区的志愿者队伍,请用画树状图或列表的方法求他和小红的爸爸被分到同一组的概率.21. 如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
(1)、若 , 求反比例函数解析式;(2)、连接并延长交反比例函数图象的另一分支于点 , 连接交轴于点 , 若 , 求的面积.20. 小红的爸爸积极参加社区志愿服务工作.根据社区安排,志愿者被随机分到组(清除小广告)、组(便民代购)和组(环境消杀).(1)、小红爸爸被分到组的概率是;(2)、某中学王老师也参加了该社区的志愿者队伍,请用画树状图或列表的方法求他和小红的爸爸被分到同一组的概率.21. 如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)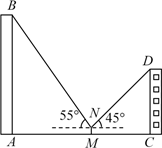 22. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、更便捷.为此,李老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种).某校九年级(1)班同学利用周末对全校师生进行了随机访问,并将统计结果绘制成两幅不完整的统计图,请结合图中所给的信息解答下列问题:
22. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、更便捷.为此,李老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种).某校九年级(1)班同学利用周末对全校师生进行了随机访问,并将统计结果绘制成两幅不完整的统计图,请结合图中所给的信息解答下列问题: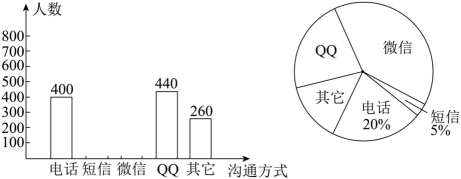 (1)、这次参与调查的共有人,在扇形统计图中,表示“微信”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、如果该校有6000人在使用手机,请估计该校最喜欢用“微信”进行沟通的人数.23. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD.
(1)、这次参与调查的共有人,在扇形统计图中,表示“微信”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、如果该校有6000人在使用手机,请估计该校最喜欢用“微信”进行沟通的人数.23. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD. (1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.24. 某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.(1)、用含x的代数式表示:每件商品的销售价为元,每件商品的利润为元,每周的商品销售量为件;(2)、求y关于x的函数关系式(不要求写出x的取值范围);(3)、应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
(1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.24. 某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.(1)、用含x的代数式表示:每件商品的销售价为元,每件商品的利润为元,每周的商品销售量为件;(2)、求y关于x的函数关系式(不要求写出x的取值范围);(3)、应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?