江西省赣北学考联盟2023年中考一模数学试卷
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
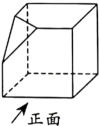
1. 2023的倒数是( )A、2023 B、 C、-2023 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图所示,将一个正方体切去一个角,则所得几何体的左视图为( )
 A、
A、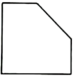 B、
B、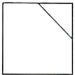 C、
C、 D、
D、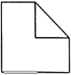 4. 下列说法正确的是( )A、为了加强“五项管理”,要了解某市中学生的睡眠时间,采用全面调查 B、打开电视机,它正在播广告是必然事件 C、一组数据“5,4,6,2,7,4,3”的众数是4,中位数是2 D、甲、乙两名同学5次数学测试的平均数都是92分,方差分别为 , , 由此可以判断甲的数学成绩比乙的稳定5. 两个直角三角板如图摆放,其中 , , , AB与DF交于点M.若 , 则的大小为( )
4. 下列说法正确的是( )A、为了加强“五项管理”,要了解某市中学生的睡眠时间,采用全面调查 B、打开电视机,它正在播广告是必然事件 C、一组数据“5,4,6,2,7,4,3”的众数是4,中位数是2 D、甲、乙两名同学5次数学测试的平均数都是92分,方差分别为 , , 由此可以判断甲的数学成绩比乙的稳定5. 两个直角三角板如图摆放,其中 , , , AB与DF交于点M.若 , 则的大小为( )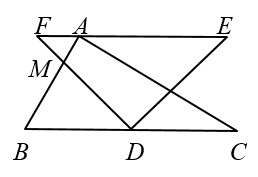 A、 B、 C、 D、6. 如图,抛物线()的对称轴为直线 , 与轴的一个交点在和之间,其部分图象如图所示,则下列结论:(1);(2);(3);(4);(5)点 , , 是该抛物线上的点,则;其中正确结论的个数是( )
A、 B、 C、 D、6. 如图,抛物线()的对称轴为直线 , 与轴的一个交点在和之间,其部分图象如图所示,则下列结论:(1);(2);(3);(4);(5)点 , , 是该抛物线上的点,则;其中正确结论的个数是( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
7. 在实数范围内分解因式:xy2﹣4x=.8. 甲型H1N1流感病毒的直径约是0.00000011米,用科学记数法表示为米.9. 已知 , 是方程的两根,则的值为 .10. 《孙子算经》有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸.问竿长几何?”歌谣的意思是:有一根竹笨不知道有多长,量出它在太阳下的影子长一丈五.同时立一根一尺五的小标杆,它的影长五寸.请你算一算竹竿的长度是尺.(1丈等于10尺,1尺等于10寸)11. 如图,等腰三角形的底边长为4,面积是20,腰的垂直平分线分别交 , 边于 , 点.若点为边的中点,点为线段上一动点,则周长的最小值为 .
 12. 在菱形中, , , , 分别是 , 的中点,动点从出发,沿着顺时针方向运动到点,当为直角三角形时,的长度为 .
12. 在菱形中, , , , 分别是 , 的中点,动点从出发,沿着顺时针方向运动到点,当为直角三角形时,的长度为 .
三、解答题
-
13.(1)、计算:(2)、解不等式组14. 先化简再求值: , 其从 , 2, , 3中选一个合适的数代入求值.15. “垃圾分类”进校园,锦江教育出实招.锦江区编写小学生《垃圾分类校本实施指导手册》,给同学们介绍垃圾分类科学知识,要求大家将垃圾按A,B,C,D四类分别装袋投放.其中A类指有害垃圾,B类指厨余垃圾,C类指可回收垃圾,D类指其他垃圾.小明和小亮各有一袋垃圾,需投放到小区如图所示的垃圾桶.(1)、“小明投放的垃圾恰好是有害垃圾”这一事件是.(请将正确答案的序号填写在横线上)
①必然事件 ②不可能事件 ③随机事件
(2)、请用列表或画树状图的方法,求小明与小亮投放的垃圾是同类垃圾的概率.A.有害垃圾
 B.厨余垃圾
B.厨余垃圾 
C.可回收垃圾
 D.其他垃圾
D.其他垃圾  16. 如图,四边形中, , , , 请用无刻度的直尺按要求画图(不写做法,保留作图痕迹).
16. 如图,四边形中, , , , 请用无刻度的直尺按要求画图(不写做法,保留作图痕迹). (1)、在图1中,画出的中点 .(2)、在图2中,画出的中点 .17. 某公司计划购进多种优质特产水果加工成水果套餐进行销售,以3万元/吨的价格买入,包装后直接销售,它的平均销售价格(单位:万元/吨)是销售数量( , 单位:吨)的一次函数,并且当时 , 当时 , 已知包装费用为1万元/吨.(1)、求与的函数关系式;(2)、当销售数量为多少时,该经营这批套餐所获得的毛利润()最大?最大毛利润为多少万元?(毛利润=销售总收入-进价总成本-包装总费用)18. 如图,已知一次函数的图象与轴、轴分别交于、两点,与反比例函数的图象分别交于、两点,点 , 点是线段的中点.
(1)、在图1中,画出的中点 .(2)、在图2中,画出的中点 .17. 某公司计划购进多种优质特产水果加工成水果套餐进行销售,以3万元/吨的价格买入,包装后直接销售,它的平均销售价格(单位:万元/吨)是销售数量( , 单位:吨)的一次函数,并且当时 , 当时 , 已知包装费用为1万元/吨.(1)、求与的函数关系式;(2)、当销售数量为多少时,该经营这批套餐所获得的毛利润()最大?最大毛利润为多少万元?(毛利润=销售总收入-进价总成本-包装总费用)18. 如图,已知一次函数的图象与轴、轴分别交于、两点,与反比例函数的图象分别交于、两点,点 , 点是线段的中点.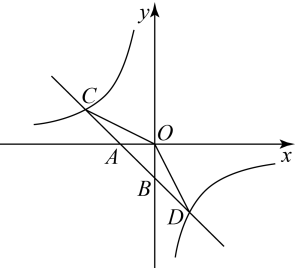 (1)、求一次函数与反比例函数的解析式;(2)、求的面积;(3)、直接写出时自变量的取值范围.19. 某校为了七、八、九年级学生对“创建文明城市”知识的掌握情况,从七、八、九年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
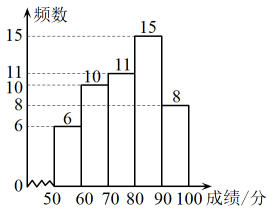
(1)、求一次函数与反比例函数的解析式;(2)、求的面积;(3)、直接写出时自变量的取值范围.19. 某校为了七、八、九年级学生对“创建文明城市”知识的掌握情况,从七、八、九年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:a.九年级成绩频数分布直方图
b.九年级成绩在 70≤x<80 这一组的是:71 73 74 74 75 75 76 76 76 77 78
c.七、八、九年级成绩的平均数、中位数如下:
年级
平均数
中位数
七
75.9
77
八
77.2
78.5
九
77.5
根据以上信息,回答下列问题:
(1)、在这次测试中,九年级在70分以上(含70分)的有人;(2)、表中的值为;(3)、在这次测试中,七年级学生甲、八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)、该校九年级学生有450人,假设全部参加此次测试,请估计九年级成绩超过平均数77.5分的人数.20. 如今,不少人在购买家具时追求简约大气的风格,图1所示的是一款非常畅销的简约落地收纳镜,其支架的形状固定不变,镜面可随意调节,图2所示的是其侧面示意图,其中OD为镜面,EF为放置物品的收纳架,AB,AC为等长的支架,BC为水平地面,已知OA=BD=40cm,OD=120cm, . (结果精确到1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,≈1.41,≈1.73)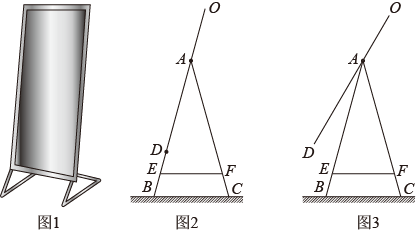 (1)、求支架顶点A到地面BC的距离;(2)、如图3,将镜面顺时针旋转15°,求此时收纳镜顶部端点O到地面BC的距离.21. 如图,在中, , 以为直径的分别与 , 交于点 , , 过点作 , 垂足为点 .
(1)、求支架顶点A到地面BC的距离;(2)、如图3,将镜面顺时针旋转15°,求此时收纳镜顶部端点O到地面BC的距离.21. 如图,在中, , 以为直径的分别与 , 交于点 , , 过点作 , 垂足为点 . (1)、求证:直线是的切线;(2)、求证:;(3)、若的半径为8, , 求扇形(阴影部分)的周长(结果保留).22. 如图所示,抛物线经过A、两点,A、两点的坐标分别为 , . 点为抛物线的顶点,点为抛物线与轴的另一交点.
(1)、求证:直线是的切线;(2)、求证:;(3)、若的半径为8, , 求扇形(阴影部分)的周长(结果保留).22. 如图所示,抛物线经过A、两点,A、两点的坐标分别为 , . 点为抛物线的顶点,点为抛物线与轴的另一交点. (1)、求点坐标;(2)、是抛物线在第四象限部分的一个动点,求四边形面积的最大值;(3)、若坐标为 , 在直线上存在点 , 使得以、、为顶点的三角形与相似,请你直接写出所有满足条件的点的坐标.23. 【课本再现】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点为线段的黄金分割点.
(1)、求点坐标;(2)、是抛物线在第四象限部分的一个动点,求四边形面积的最大值;(3)、若坐标为 , 在直线上存在点 , 使得以、、为顶点的三角形与相似,请你直接写出所有满足条件的点的坐标.23. 【课本再现】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点为线段的黄金分割点. (1)、【问题发现】如图1,请直接写出与的比值是;(2)、【尺规作黄金分割点】如图2,在中, , , , 则 , 在上截取 , 则 , 在上截取 , 则的值为;(3)、【问题解决】如图3,用边长为4的正方形纸片进行如下操作:对折正方形得折痕 , 连接 , 点对应点 , 得折痕 , 试说明:是的黄金分割点;(4)、【拓展延伸】如图4,正方形中,为对角线上一点,点在边上,且 , 当为的黄金分割点时, , 连 , 延长交于 , 请用相似的知识求出的值为 .
(1)、【问题发现】如图1,请直接写出与的比值是;(2)、【尺规作黄金分割点】如图2,在中, , , , 则 , 在上截取 , 则 , 在上截取 , 则的值为;(3)、【问题解决】如图3,用边长为4的正方形纸片进行如下操作:对折正方形得折痕 , 连接 , 点对应点 , 得折痕 , 试说明:是的黄金分割点;(4)、【拓展延伸】如图4,正方形中,为对角线上一点,点在边上,且 , 当为的黄金分割点时, , 连 , 延长交于 , 请用相似的知识求出的值为 .