河北省唐山市丰润区2023年九年级中考模拟数学试卷
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
1. 经过直线外一点的5条不同的直线中,与直线相交的直线至少有( )A、2条 B、3条 C、4条 D、5条2. 如图,在中, , 则下列说法中,正确的是( )
 A、是的中线 B、是的角平分线 C、是的高线 D、是的中线3. 与互为倒数的是( )A、 B、 C、 D、4. 不等式组的解集在数轴上表示正确的是( )A、
A、是的中线 B、是的角平分线 C、是的高线 D、是的中线3. 与互为倒数的是( )A、 B、 C、 D、4. 不等式组的解集在数轴上表示正确的是( )A、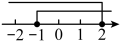 B、
B、 C、
C、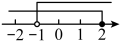 D、
D、 5. ( )A、 B、 C、 D、6. 将点沿水平方向向右平移4个单位长度再向下平移2个单位长度得到点 , 若点在直线上,则的值为( )A、6 B、5 C、-6 D、-57. 在平面直角坐标系中,点的坐标是 , 连接 , 将线段绕原点顺时针旋转90°,得到对应线段 , 则点的坐标为( )A、 B、 C、 D、8. 如图,电线杆的中点处有一标志物,在地面点处测得标志物的仰角为35°,若拉线的长度是米,则电线杆的长可表示为( )
5. ( )A、 B、 C、 D、6. 将点沿水平方向向右平移4个单位长度再向下平移2个单位长度得到点 , 若点在直线上,则的值为( )A、6 B、5 C、-6 D、-57. 在平面直角坐标系中,点的坐标是 , 连接 , 将线段绕原点顺时针旋转90°,得到对应线段 , 则点的坐标为( )A、 B、 C、 D、8. 如图,电线杆的中点处有一标志物,在地面点处测得标志物的仰角为35°,若拉线的长度是米,则电线杆的长可表示为( ) A、米 B、米 C、米 D、米9. 如图,边长为的长方形周长为12,面积为5,则的值为( )
A、米 B、米 C、米 D、米9. 如图,边长为的长方形周长为12,面积为5,则的值为( )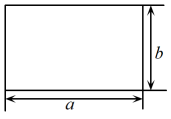 A、60 B、120 C、130 D、24010. 估计的值在数轴上最可能表示的点是( )
A、60 B、120 C、130 D、24010. 估计的值在数轴上最可能表示的点是( ) A、 B、 C、 D、11. 如图,矩形在外接圆与水平地面相切于点 , 已知圆的半径为4,且 . 若在没有滑动的情况下,将圆向右滚动,使得点向右移动了 , 则此时与地面相切的弧为( )
A、 B、 C、 D、11. 如图,矩形在外接圆与水平地面相切于点 , 已知圆的半径为4,且 . 若在没有滑动的情况下,将圆向右滚动,使得点向右移动了 , 则此时与地面相切的弧为( ) A、 B、 C、 D、12. 抛物线的顶点一定不在第( )象限.A、一 B、二 C、三 D、四13. “共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值),则下列说法正确的是( )
A、 B、 C、 D、12. 抛物线的顶点一定不在第( )象限.A、一 B、二 C、三 D、四13. “共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值),则下列说法正确的是( ) A、小文一共抽样调查了20人 B、样本中当月使用“共享单车” 次的人数最多 C、样本中当月使用“共享单车”不足30次的人数有14人 D、样本中当月使用次数不足30次的人数多于 次的人数14. 如图,中, , , 尺规作图痕迹如下.
A、小文一共抽样调查了20人 B、样本中当月使用“共享单车” 次的人数最多 C、样本中当月使用“共享单车”不足30次的人数有14人 D、样本中当月使用次数不足30次的人数多于 次的人数14. 如图,中, , , 尺规作图痕迹如下.结论Ⅰ:点一定为的内心;
结论Ⅱ:连接 , , 则 .
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
 A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对,Ⅱ对 D、Ⅰ对,Ⅱ不对15. 如图,直线l上有三点A,B,C, , , 点P,Q分别从点A,B同时出发,向点C移动,点P的速度是m个单位长/秒,点Q的速度是n个单位长/秒, , 那么( )
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对,Ⅱ对 D、Ⅰ对,Ⅱ不对15. 如图,直线l上有三点A,B,C, , , 点P,Q分别从点A,B同时出发,向点C移动,点P的速度是m个单位长/秒,点Q的速度是n个单位长/秒, , 那么( ) A、点P先到 B、点Q先到 C、点P,Q同时到 D、无法确定哪点先到16. 如图,矩形中, , E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点, , 连接 , . 甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.
A、点P先到 B、点Q先到 C、点P,Q同时到 D、无法确定哪点先到16. 如图,矩形中, , E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点, , 连接 , . 甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.甲:存在点E,使;
乙:的面积存在最小值.
下列说法正确的是( )
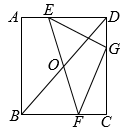 A、甲、乙都正确 B、甲、乙都错误 C、甲正确,乙错误 D、甲错误,乙正确
A、甲、乙都正确 B、甲、乙都错误 C、甲正确,乙错误 D、甲错误,乙正确二、填空题
-
17. 将一副三角尺如图所示叠放在一起,若重叠部分的面积是 , 则的长是 .
 18. 如图,以圆的半径为边分别作正五边形和正六边形 , 则°,若图中阴影部分的面积为 , 则圆的半径长是 .
18. 如图,以圆的半径为边分别作正五边形和正六边形 , 则°,若图中阴影部分的面积为 , 则圆的半径长是 . 19. 在平面直角坐标系中,直线 , 经过点 , 且与坐标轴围成的三角形的面积是9,与曲线的图象交于两点.(1)、则直线的表达式为;(2)、横、纵坐标都是整数的点叫作整点.记图象在点之间的部分与线段围成的区域(不含边界)为 . 则区域内的整点的坐标是;(3)、不等式的解集是 .
19. 在平面直角坐标系中,直线 , 经过点 , 且与坐标轴围成的三角形的面积是9,与曲线的图象交于两点.(1)、则直线的表达式为;(2)、横、纵坐标都是整数的点叫作整点.记图象在点之间的部分与线段围成的区域(不含边界)为 . 则区域内的整点的坐标是;(3)、不等式的解集是 .三、解答题
-
20. 已知:整式 .(1)、化简整式;(2)、若 ,
①求整式;
②在“□”的“□”内,填入“ , , , ”中的一个运算符号,经过计算发现,结果是不含一次项的整式,请你写出一个符合要求的算式,并计算出结果.
21. 某校七、八年级共有600名学生,为了解该校七、八年级学生对诗词知识的掌握情况,从七、八年级学生中各随机抽取15人进行诗词知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀);相关数据统计、整理如下:七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
年级
七年级
八年级
平均数
8
8
众数
8
中位数
8
优秀率
80%
60%
(1)、填空:a= , b=;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生诗词知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对诗词知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的3名学生中随机抽取2人参加市诗词知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.22. 某零售店销售甲、乙两种蔬菜,甲种蔬菜每千克获利1.1元,乙种蔬菜每千克获利1.5元.该店计划一次购进这两种蔬菜共60千克,并能全部售出.设该店购进甲种蔬菜千克,销售这60千克蔬菜获得的总利润为元.(1)、求与的关系式;(2)、若乙种蔬菜的进货量不超过甲种蔬菜的 , 则该店购进甲、乙两种蔬菜各多少千克时,获得的总利润最大?(3)、由于蔬菜自身的特点,有的乙种蔬菜需要保鲜处理,每千克的保鲜费用是元().若获得的总利润随的增大而减小,请直接写出的取值范围.23. 如图,把两个扇形与扇形的圆心重合叠放在一起,且 , 连接 . (1)、求证:;(2)、若 , 弧的长为 , 弧的长为 , 求阴影部分的面积;(3)、在(2)的条件下求由扇形围成的圆锥的高.24. 已知,在Rt中, , 点是斜边的中点, , 且 , 于点 , 连结 .
(1)、求证:;(2)、若 , 弧的长为 , 弧的长为 , 求阴影部分的面积;(3)、在(2)的条件下求由扇形围成的圆锥的高.24. 已知,在Rt中, , 点是斜边的中点, , 且 , 于点 , 连结 . (1)、求证: ;(2)、当时,求的值;(3)、在(2)的条件下,求的值.25. 城市绿化部门定期安排洒水车为公路两侧绿化带浇水,如图1,洒水车沿着平行于公路路牙方向行驶,喷水口离地竖直高度为 . 如图2,可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度 . 内边缘抛物线是由外边缘抛物线向左平移得到,外边抛物线最高点离喷水口的水平距离为 , 高出喷水口 ,
(1)、求证: ;(2)、当时,求的值;(3)、在(2)的条件下,求的值.25. 城市绿化部门定期安排洒水车为公路两侧绿化带浇水,如图1,洒水车沿着平行于公路路牙方向行驶,喷水口离地竖直高度为 . 如图2,可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度 . 内边缘抛物线是由外边缘抛物线向左平移得到,外边抛物线最高点离喷水口的水平距离为 , 高出喷水口 , (1)、求外边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求内边缘抛物线与轴的正半轴交点的坐标;(3)、当时,判断洒水车行驶时喷出的水能否浇灌到整个绿化带,并说明理由.26. 如图1, , , 点在上,点在上,于点 , 是半圆的直径,且 , 为上靠近点的三等分点,是上的动点.
(1)、求外边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求内边缘抛物线与轴的正半轴交点的坐标;(3)、当时,判断洒水车行驶时喷出的水能否浇灌到整个绿化带,并说明理由.26. 如图1, , , 点在上,点在上,于点 , 是半圆的直径,且 , 为上靠近点的三等分点,是上的动点. (1)、的最小值为 , 的最大值为;(2)、沿直线向右平移半圆 , 若半圆的右移速度为每秒1个单位长,求点在的区域内部(包括边界)的时长;(3)、过点作于点 , 且 , 沿直线向右平移半圆 .
(1)、的最小值为 , 的最大值为;(2)、沿直线向右平移半圆 , 若半圆的右移速度为每秒1个单位长,求点在的区域内部(包括边界)的时长;(3)、过点作于点 , 且 , 沿直线向右平移半圆 .①如图2,当点与点重合时,求半圆在上截得的线段的长;
②将半圆移动到如图2所示的位置时作为初始位置,将线段连带半圆按顺时针方向开始旋转,如图3所示,设旋转角为 . 当半圆与的边相切时,直接写出点运动的路径长.(注:结果保留 , , )