广东省深圳市坪山区2023年中考一模数学试卷
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
1. 的值为( )A、1 B、 C、 D、2. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列一元二次方程中,有两个相等的实数根的是( )A、 B、 C、 D、4. 在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )A、15个 B、20个 C、30个 D、35个5. 如图,点 , , 是上的三个点,若 , 则的度数为( )
3. 下列一元二次方程中,有两个相等的实数根的是( )A、 B、 C、 D、4. 在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )A、15个 B、20个 C、30个 D、35个5. 如图,点 , , 是上的三个点,若 , 则的度数为( ) A、76° B、38° C、24° D、33°6. 把二次函数先向右平移2个单位长度,再向上平移1个单位长度,新二次函数表达式变为( )A、 B、 C、 D、7. 如图,在菱形中,对角线 , 相交于点 , 添加下列条件,能使菱形成为正方形的是( )
A、76° B、38° C、24° D、33°6. 把二次函数先向右平移2个单位长度,再向上平移1个单位长度,新二次函数表达式变为( )A、 B、 C、 D、7. 如图,在菱形中,对角线 , 相交于点 , 添加下列条件,能使菱形成为正方形的是( ) A、 B、 C、 D、平分8. 如图,扇形AOB 中,半径OA=2,∠AOB=120°,C 是的中点,连接AC、BC,则图中阴影部分面积是 ( )
A、 B、 C、 D、平分8. 如图,扇形AOB 中,半径OA=2,∠AOB=120°,C 是的中点,连接AC、BC,则图中阴影部分面积是 ( ) A、 B、 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax﹣2b(a≠0)与反比例函数y= (c≠0)在同一平面直角坐标系中的图象大致是( )
A、 B、 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax﹣2b(a≠0)与反比例函数y= (c≠0)在同一平面直角坐标系中的图象大致是( ) A、
A、 B、
B、 C、
C、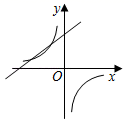 D、
D、 10. 如图,正方形的边长为12,E是中点,F是对角线上一点,且 , 在上取点G,使得 , 交于H,则的长为( )
10. 如图,正方形的边长为12,E是中点,F是对角线上一点,且 , 在上取点G,使得 , 交于H,则的长为( ) A、4 B、 C、 D、
A、4 B、 C、 D、二、填空题
-
11. 抛物线y=2(x-3)2+1的顶点坐标为 .12. 如图是拦水坝的横断面,斜坡的水平宽度为12米,斜面坡度为 , 则斜坡的长为米.
 13. 图①是伸缩折叠不锈钢晾衣架的实物图,图②是它的侧面示意图,和相交于点O,点A、B之间的距离为米, , 根据图②中的数据可得C、D之间的距离为米.
13. 图①是伸缩折叠不锈钢晾衣架的实物图,图②是它的侧面示意图,和相交于点O,点A、B之间的距离为米, , 根据图②中的数据可得C、D之间的距离为米.
 14. 如图,点A,C为函数图象上的两点,过A,C分别作轴,轴,垂足分别为B,D,连接 , , , 线段交于点E,且点E恰好为的中点.当的面积为时,k的值为 .
14. 如图,点A,C为函数图象上的两点,过A,C分别作轴,轴,垂足分别为B,D,连接 , , , 线段交于点E,且点E恰好为的中点.当的面积为时,k的值为 .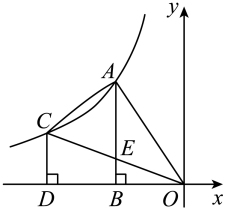 15. 如图,在矩形中,点E为上一点, , , 连接 , 将沿所在的直线翻折,得到 , 交于点F,将沿所在的直线翻折,得到 , 交于点G,的值为 .
15. 如图,在矩形中,点E为上一点, , , 连接 , 将沿所在的直线翻折,得到 , 交于点F,将沿所在的直线翻折,得到 , 交于点G,的值为 .
三、解答题
-
16. 计算: .17. 小明购买了“二十四节气”主题邮票,他将“立春”“清明”“雨水”三张纪念邮票(除正面内容不同,其余均相同)背面朝上,洗匀放好.
 (1)、小明从中随机抽取一张邮票是“立春”的概率是 .(2)、小明从中随机抽取一张邮票,记下内容后,正面向下放回,洗匀后再从中随机抽取一张邮票,请用画树状图或列表的方法,求小明两次抽取的邮票中至少有一张是“雨水”的概率(这三张邮票依次分别用字母A,B,C表示).18. 数学活动小组到某广场测量标志性建筑的高度.如图,他们在地面上C点测得最高点A的仰角为 , 再向前至D点,又测得最高点A的仰角为 , 点C,D,B在同一直线上,求该建筑物的高度.(参考数据: , , )
(1)、小明从中随机抽取一张邮票是“立春”的概率是 .(2)、小明从中随机抽取一张邮票,记下内容后,正面向下放回,洗匀后再从中随机抽取一张邮票,请用画树状图或列表的方法,求小明两次抽取的邮票中至少有一张是“雨水”的概率(这三张邮票依次分别用字母A,B,C表示).18. 数学活动小组到某广场测量标志性建筑的高度.如图,他们在地面上C点测得最高点A的仰角为 , 再向前至D点,又测得最高点A的仰角为 , 点C,D,B在同一直线上,求该建筑物的高度.(参考数据: , , ) 19. 某电商在抖音平台上对红富士苹果进行直播销售.已知苹果的成本价为6元/千克,如果按10元/千克销售,每天可卖出160千克.通过调查发现,每千克苹果售价增加1元,日销售量减少20千克.(1)、为保证每天利润为700元,商家想尽快销售完库存,每千克售价应为多少元?(2)、售价为多少元时,每天的销售利润最大,最大是多少?20. 如图,在中, , 以为直径作 , 交于点F,过C点作交延长线于点D,E为上一点,且 .
19. 某电商在抖音平台上对红富士苹果进行直播销售.已知苹果的成本价为6元/千克,如果按10元/千克销售,每天可卖出160千克.通过调查发现,每千克苹果售价增加1元,日销售量减少20千克.(1)、为保证每天利润为700元,商家想尽快销售完库存,每千克售价应为多少元?(2)、售价为多少元时,每天的销售利润最大,最大是多少?20. 如图,在中, , 以为直径作 , 交于点F,过C点作交延长线于点D,E为上一点,且 . (1)、求证:为的切线;(2)、若 , 求的长.21. 在平面直角坐标系中,若两点的横坐标不相等,纵坐标互为相反数,则称这两点关于x轴斜对称,其中一点叫做另一点关于x轴的斜对称点.如:点 , 关于x轴斜对称,在平面直角坐标系中,点A的坐标为 .
(1)、求证:为的切线;(2)、若 , 求的长.21. 在平面直角坐标系中,若两点的横坐标不相等,纵坐标互为相反数,则称这两点关于x轴斜对称,其中一点叫做另一点关于x轴的斜对称点.如:点 , 关于x轴斜对称,在平面直角坐标系中,点A的坐标为 . (1)、下列各点中,与点A关于x轴斜对称的点是(只填序号);
(1)、下列各点中,与点A关于x轴斜对称的点是(只填序号);① , ② , ③ , ④ .
(2)、若点A关于x轴的斜对称点B恰好落在直线上,的面积为3,求k的值;(3)、抛物线上恰有两个点M、N与点A关于x轴斜对称,抛物线的顶点为D,且为等腰直角三角形,则b的值为 .22. 将正方形的边绕点A逆时针旋转至 , 记旋转角为 , 连接 , 过点B作直线 , 垂足为点F,连接 . (1)、如图1,当时,的形状为 , 的值为;(2)、当时,
(1)、如图1,当时,的形状为 , 的值为;(2)、当时,①(1)中的两个结论是否仍然成立?如果成立,请根据图2的情形进行证明;如果不成立,请说明理由;
②如图3,正方形边长为4, , , 在旋转的过程中,是否存在与相似?若存在,则的值为 ▲ , 若不存在,请说明理由.