安徽省宿州市2023年中考一模数学试题
试卷更新日期:2023-04-24 类型:中考模拟
一、单选题
-
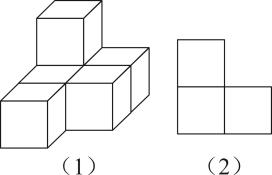
1. 下列比-1小的数是( )A、0 B、-2023 C、1 D、2. 由几个小立方体搭成的一个几何体如图(1)所示,它的主(正)视图如图(2)所示,则它的俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 2022年,采矿业实现利润总额15573.6亿元,比上年增长制造业实现利润总额64150.2亿元,下降;电力、热力、燃气及水生产和供应业实现利润总额4314.7亿元,增长 . 其中数据亿用科学记数法表示为( )A、 B、 C、 D、4. 计算的结果正确的是( )A、 B、 C、 D、5. 将含角的直角三角板如图放置,使其三个顶点分别落在三条平行直线上,其中 . 若 , 则的度数为( )
3. 2022年,采矿业实现利润总额15573.6亿元,比上年增长制造业实现利润总额64150.2亿元,下降;电力、热力、燃气及水生产和供应业实现利润总额4314.7亿元,增长 . 其中数据亿用科学记数法表示为( )A、 B、 C、 D、4. 计算的结果正确的是( )A、 B、 C、 D、5. 将含角的直角三角板如图放置,使其三个顶点分别落在三条平行直线上,其中 . 若 , 则的度数为( ) A、 B、 C、 D、6. 下列各式中,可以在有理数范围内进行因式分解的是( )A、 B、 C、 D、7. 如图,是的直径,弦于点 . 若 , 则的长为( )
A、 B、 C、 D、6. 下列各式中,可以在有理数范围内进行因式分解的是( )A、 B、 C、 D、7. 如图,是的直径,弦于点 . 若 , 则的长为( )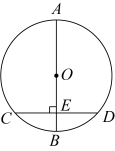 A、 B、 C、1 D、28. 在一个桌子上放着若干张背面向上的扑克牌,这些扑克牌背面图案相同,正面为3张方块、2张红桃和张梅花.若从这些打乱的扑克牌中任意摸出1张扑克牌,这张扑克牌是梅花的概率为 , 则的值为( )A、4 B、5 C、6 D、79. 若拋物线的顶点在第二象限,则的取值范围是( )A、 B、 C、 D、10. 如图,点在正方形边上,点在边的延长线上, , 过点作的垂线与的延长线交于点 . 若 , 则正方形的边长为( )
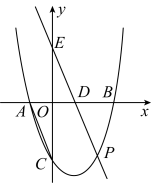
A、 B、 C、1 D、28. 在一个桌子上放着若干张背面向上的扑克牌,这些扑克牌背面图案相同,正面为3张方块、2张红桃和张梅花.若从这些打乱的扑克牌中任意摸出1张扑克牌,这张扑克牌是梅花的概率为 , 则的值为( )A、4 B、5 C、6 D、79. 若拋物线的顶点在第二象限,则的取值范围是( )A、 B、 C、 D、10. 如图,点在正方形边上,点在边的延长线上, , 过点作的垂线与的延长线交于点 . 若 , 则正方形的边长为( )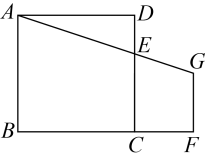 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
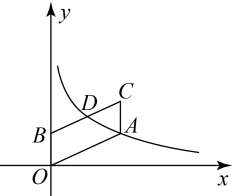
11. 计算:.12. 命题“如果 , 那么”的逆命题为 .13. 如图,反比例函数的图象经过点 , 连接 , 把线段向上平移个单位得到线段 , 与反比例函数的图象交于点 . 若点是的中点,则的值为 .
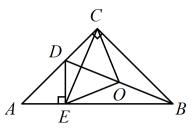
 14. 如图,在中, , , 是边上的高,过点作 , 且 , 点与点均在的右侧,连接 , 交于点 .
14. 如图,在中, , , 是边上的高,过点作 , 且 , 点与点均在的右侧,连接 , 交于点 .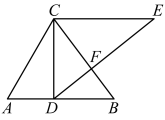 (1)、若点为的中点,则的长为;(2)、若 , 则的长为 .
(1)、若点为的中点,则的长为;(2)、若 , 则的长为 .三、解答题
-
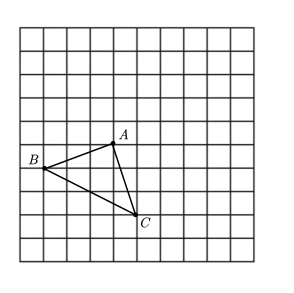
15. 计算: .16. 如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中为格点三角形.
 (1)、在图中作出点关于直线对称的点;(2)、以点为旋转中心,作出将顺时针旋转后得到的 , 其中点与点对应,点与点对应.17. 2022年7月,河南安阳等地遭遇特大暴雨袭击,暴雨中有房屋倒塌,道路被冲毁,车辆被冲走.灾情发生后,全国各地纷纷援助.合肥某公司筹集了一批物资,准备运往灾区,计划租用甲、乙两种型号的货车,在每辆货车都满载的情况下,若租用30辆甲型货车和50辆乙型货车可装载1500箱物资;若租用20辆甲型货车和60辆乙型货车可装载1400箱物资.求出甲、乙两种型号的货车每辆分别可装载多少箱物资?18. 观察下列等式:
(1)、在图中作出点关于直线对称的点;(2)、以点为旋转中心,作出将顺时针旋转后得到的 , 其中点与点对应,点与点对应.17. 2022年7月,河南安阳等地遭遇特大暴雨袭击,暴雨中有房屋倒塌,道路被冲毁,车辆被冲走.灾情发生后,全国各地纷纷援助.合肥某公司筹集了一批物资,准备运往灾区,计划租用甲、乙两种型号的货车,在每辆货车都满载的情况下,若租用30辆甲型货车和50辆乙型货车可装载1500箱物资;若租用20辆甲型货车和60辆乙型货车可装载1400箱物资.求出甲、乙两种型号的货车每辆分别可装载多少箱物资?18. 观察下列等式:第1个等式:;
第2个等式:;
第3个等式:
第4个等式: ,
……
请根据以上规律,解决下列问题
(1)、试写出第5个等式;(2)、请证明第4个等式.19. 如图是某段河道的坡面横截面示意图,从点到点 , 从点到点是两段不同坡度的坡路,是一段水平路段,为改建成河道公园,改善居民生活环境,决定按照的坡度降低坡面的坡度,得到新的山坡 , 经测量获得如下数据:与水平面的距离为 , 坡面的长为 , , 坡面与水平面的夹角为 , 降低坡度后,三点在同一条直线上,即 . 为确定施工点的位置,试求坡面的长和的长度( , , , , , , 结果精确到0.1米)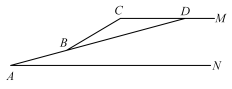 20. 阿基米德(公元前287年-公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,阿基米德流传于世的著作有10余种,多为希腊文手稿.下面是《阿基米德全集》中记载的一个命题:如图1,是的弦,点在上,且于点 , 在弦上取点 , 使 , 点是上的一点,且 , 连接 , 求证: .
20. 阿基米德(公元前287年-公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,阿基米德流传于世的著作有10余种,多为希腊文手稿.下面是《阿基米德全集》中记载的一个命题:如图1,是的弦,点在上,且于点 , 在弦上取点 , 使 , 点是上的一点,且 , 连接 , 求证: .
学习小组中的一位同学进行了如下证明:
如图2,连接 , ,
∵ , .
∴
∵ ,
∴
……
请完成下列的任务:
(1)、完成上面的证明:(2)、如图3,将上述问题中弦改为直径 , 若 , 求证点是的中点.21. 为庆祝中国共产党第二十次全国代表大会胜利石开,某中学组织了“共和国成就”知识竞赛,校团委李老师随机调查了部分同学的竞赛成绩,并将他们的成绩(百分制)进行整理、描述和分析,部分信息如下(单位:分):.将成绩分为(优秀),(良好),(合格),(不合格)四个等级,并绘制了如下两幅不完整的统计图.
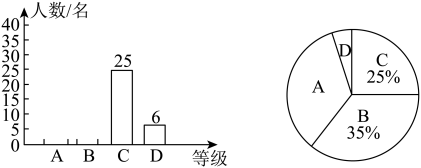
.组的同学具体得分是68,54,65,55,65,59.
根据以上信息,回答下列问题:
(1)、本次抽样调查的样本容量是 ▲ , 请补全条形统计图;(2)、组数据中的平均数为 , 中位数为;(3)、已知组调查对象中只有两位男生竞赛成绩不合格,团委李老师准备随机回访组中两位竞赛成绩不合格的同学,请用画树状图或列表法求出恰好回访到一男一女的概率.